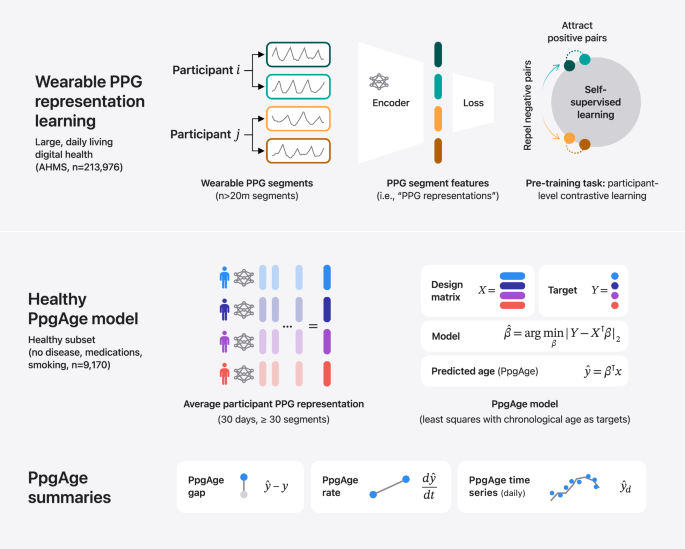
Introduction
Age is a major driver of disease and functional decline1,2 and is considered in a wide range of clinical and policy decisions—from screening for and treating disease3,4 to the determination of insurance costs and retirement benefits5,6. Yet age-related decline can vary markedly from individual to individual7,8. It is not uncommon for a physician to assess a patient’s “apparent age” relative to their “stated age”9,10, suggesting some unmeasured aging process informative of patient health. And while a clinician’s first impression may elude standardization, the idea that appearing older (or younger) might carry prognostic value motivates the construction of a more objective biological aging clock.
Biological aging generally refers to the constellation of changes due to the consequences of biological processes and daily living, leading to changes in physiology, functional decline, disease, and ultimately mortality11,12,13. While the typical treatment strategy for age-related chronic disease focuses on the specific condition, the geroscience hypothesis posits that the onset and severity of all age-related chronic disease could be delayed by slowing the process of aging itself14,15,16. The aging process, beyond simple chronological age, is challenging to measure, highlighting the need to establish biomarkers of aging that are easy to collect longitudinally, predictive of age-related decline, and responsive to longevity-targeting interventions (e.g., lifestyle, pharmacological, etc.)13. Such validated biomarkers will play a vital role in the translation of aging research into clinical practice17.
Research into aging clocks has intensified accordingly13. Seminal work proposed DNA methylation patterns as an epigenetic biomarker of aging18,19, and the resulting clocks are predictive of chronological age, chronic disease, disability, and mortality20, as well as sensitive to some longevity interventions21. More recent aging clocks leverage other—typically clinical—data modalities, including electrocardiograms (ECGs)22,23, polysomnograms (PSGs)24, electroencephalograms (EEGs)25, magnetic resonance imaging (MRI) of the brain26, fundus imaging27, labs and vitals28, and clinical photoplethysmography (PPG)29; each targeting some aspect of the multi-dimensional (and heterogeneous) process of aging. In these approaches, the underlying measurement is either invasive (e.g., blood-based labs), expensive (e.g., an MRI), or inconvenient (e.g., clinical ECG or PSG). Such data modalities limit scalability and frustrate longitudinal collection, reducing the likelihood of observing changes, inflection points, or responses to interventions.
This longitudinal scarcity has turned attention toward wearables. A recent effort to quantify aging with wearables uses step count and accelerometry correlated with blood-based biological age estimates and disease30. However, activity-focused predictors leverage behavioral changes associated with aging and can be confused by social factors that influence aging estimates. For example, Pyrkov et al.30 also find that activity-based biological age estimates sharply increased when physical activity levels dropped during the early stages of the COVID-19 pandemic.
Alternatively, wearable PPG is a sensor modality that presents an opportunity to more directly assess health and aging throughout daily living. PPG in general is a non-invasive optical measure of volumetric variation in blood circulation, using a light source and a photodetector at the surface of the skin—in wearables, this is typically at the finger or wrist29. The shape of the PPG waveform exhibits a pulsatile component attributed to changes in blood volume with each heart beat, superimposed on a slowly varying component attributed to respiration and the sympathetic nervous system31. In clinical settings, PPG (typically at the finger) is widely used in pulse oximetry, providing continuous blood oxygen measurements32, and has been incorporated into early warning systems33. Clinical PPG has also been studied in relation to aging, with a particular focus on vascular health34,35.
Consumer wearables have incorporated PPG primarily to measure heart rate (HR) and heart rate variability (HRV) (including irregular rhythms), producing estimates that have been validated against reference devices36,37, and are particularly accurate when the user is at rest38. Despite the focus on HR and HRV (derived mainly from the pulsatile component), the shape of the PPG waveform contains information about cardiac, vascular, respiratory, and autonomic nervous system function29, including atherosclerosis and arterial stiffness39. Age-related changes in cardiovascular physiology and function are well-documented, including a stiffening of the myocardium, a decrease in cardiac output, and an increase in arterial stiffness11,39. Furthermore, features of infrared finger PPG recordings are known to change with age40. As such, wearable PPG is a well-motivated modality for investigating cardiovascular-related signatures of aging.
In this work, we develop and study a wearable-based aging clock, which we call PpgAge. PpgAge can be measured non-invasively, inexpensively, and passively multiple times per day, producing a scalable and rich longitudinal time series of biological age estimates throughout daily life. Based on wearable PPG, PpgAge is constructed to be predictive of chronological age in a healthy cohort derived from the Apple Heart & Movement Study (AHMS), a large-scale digital health study (n = 213,593 participants spanning over 149 million participant-days at the time of study)41 (ClinicalTrials.gov Identifier NCT04198194). Because PPG recordings are high-dimensional and highly structured waveforms, and because the physiological mechanism underlying PPG morphology are not yet fully understood31, we leverage a deep learning approach to devise a succinct and sample efficient feature representation of each PPG recording. Recent work has shown this approach to be an effective way to cope with real-world variability and distill useful information from raw, multi-channel PPG waveforms42,43.
Our analysis demonstrates that PpgAge and PpgAge gap—i.e., the deviation between predicted age and chronological age—are informative summaries of participant physiology and health. We show that (i) PpgAge accurately estimates chronological age across a range of demographic subpopulations (i.e., by self-reported age, biological sex, race/ethnicity, body mass index, and disease status), predicting chronological age with MAE of 2.43 years (95% CI 2.33–2.53) in a healthy cohort, while also being accurate in the general population; (ii) the PpgAge gap is strongly associated with the diagnosis of a wide variety of chronic diseases; (iii) the PpgAge gap predicts incident heart disease events and metabolic disease diagnoses, even when controlling for common risk factors; (iv) PpgAge gap is associated with behavioral factors, including sleep, exercise, and smoking status; and (v) PpgAge exhibits sensitivity to some longitudinal physiological changes, such as pregnancy and cardiac events. PpgAge is an easy-to-measure aging clock with potential utility in longevity research and translation into clinical practice.
Results
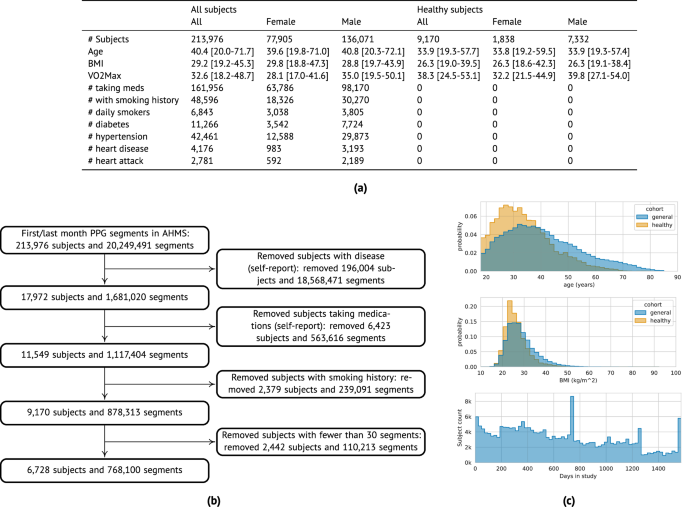
PpgAge is developed using Apple Watch PPG data collected under informed consent from participants in the AHMS41. First, we train a general-purpose deep neural network from about 20 million 60-s PPG segments via self-supervised learning (SSL), with the objective of distinguishing participants from each other, summarizing each segment with a 256-dimensional feature vector, i.e., a PPG representation42. To build a normative model of healthy aging, we select self-reported healthy participants with sufficient PPG data (n = 6728) and fit a model to predict chronological age (self-reported and approximate, see “Methods”) from the average PPG representation (i.e., 256-dimension vector) within the first 30 days of study, and separately, the last 30 days (minimum 30 segments per period, see Fig. 1 and “Methods”) using a randomly selected set of 80% (n = 5355) participants. We refer to predictions from this model as PpgAge, and the difference between PpgAge and chronological age as the PpgAge gap—higher PpgAge age gap values indicate older looking, while negative PpgAge age gap indicates younger looking. We study PpgAge estimates on the remaining healthy test cohort (n = 1373) and the general cohort (n = 120,235). We analyze the accuracy of PpgAge predictions, its cross-sectional associations with disease and behavior, and its longitudinal sensitivity to physiological changes, such as pregnancy and cardiac events (Fig. 1 and “Results” below). Figure 2a–c detail summaries of the study population and the self-reported healthy cohort, including behavioral and medical history characteristics at baseline.
Methods summary. (i) Following Abbaspourazad et al.42, we use a contrastive loss to learn PPG segment representations, a 256-dimensional vector summarizing features of a 60-s PPG segment, on a subset of 172,318 participants. (ii) PPG representations from a self-reported healthy subpopulation are used to fit a linear regression model, targeting chronological age. For a new subject, predicted age (PpgAge) is computed, and we examine the gap between PpgAge and chronological age and longitudinal changes in PpgAge time series that may co-occur with physiological changes. (iii) We analyze held out “healthy” and “general” participants, assessing accuracy of PpgAge, cross-sectional associations with disease and behavior, and longitudinal analyses of participant-level PpgAge time series.
a Summary statistics of all AHMS participants with at least one background PPG segment ("All subjects'') and the subset of participants that self report no history of disease, no medications, and no history of smoking behavior ("Healthy subjects''); see Section S1 in the Supplement for precise characterizations of these criteria. Bracketed values report interquartile range. b Inclusion/exclusion of subjects that comprise the “healthy” cohort used to train and validate age models. c Chronological age (top) and BMI (middle) distributions comparing the general and healthy cohorts, and study duration distribution (bottom) for all participants.
Wearable PPG robustly predicts chronological age via PpgAge
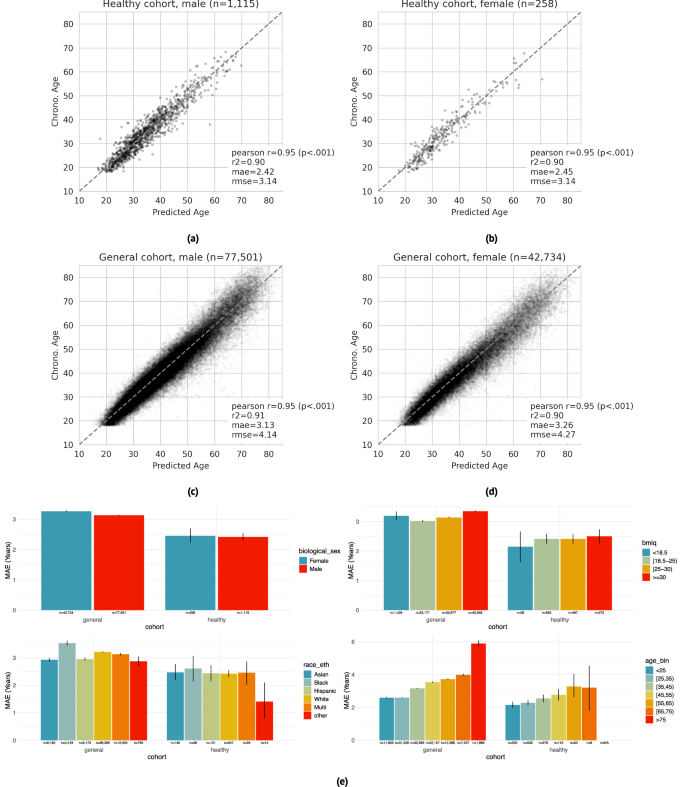
PpgAge predicts chronological age with high accuracy in both the “healthy” and “general” group. Prediction accuracy is highest in the healthy cohort, with mean absolute error (MAE) of 2.45 years (95% CI 2.22–2.71) in female participants (n = 258) and 2.42 years (95% CI 2.30–2.54) in male participants (n = 1115). In the general cohort (i.e., a distribution distinct from the training data), PpgAge predicts chronological age with MAE of 3.26 years (95% CI 3.24–3.29) among female participants (n = 42,734) and 3.13 years (95% CI 3.11–3.15) among male participants (n = 77,501). Age prediction accuracy is based on the first 30 days of PPG segments, limited to held out subjects with at least 30 PPG segments present (n = 120,235), predicting average participant age within that 30-day window. Figure 3a–d graphically summarize model predictions and error metrics.
a–d Wearable PPG segments (minimum 30 segments over a 30-day span) predict chronological age with a mean absolute error of 2.42 years (95% CI 2.30–2.54) and 2.45 years (95% CI 2.22–2.71) in healthy male and female test participants, respectively (dashed line is the identity). In the general population, prediction errors are 3.13 years (95% CI 3.11–3.15) and 3.26 years (95% CI 3.24–3.29) for male and female participants, respectively. Analysis was restricted to participants with chronological age between 18 and 85, as participants older than 75 are rare in the healthy training cohort. e Within the healthy cohort, predictions error remains relatively stable across demographic categories —biological sex (first panel), BMI (second panel), and self reported race/ethnicity (third panel). Younger participants enjoy a modestly lower error than older participants (fourth panel), which may be partially explained by a lower expectation of misdiagnosis and therefore more accurate “healthy” labels. Within the general cohort, prediction error is systematically higher and more variable, as expected as non-healthy participants were not used for training. Error bars are 95% confidence intervals computed from 1000 bootstrap replicates.
Chronological age prediction error varies little by demographic sub-population. In addition to parity between self-reported biological male and female participants, in the healthy cohort, we observe similar prediction accuracy among self-reported race/ethnicity groups (MAE 1.4–2.6 years), and self-reported BMI groups (MAE 2.1–2.5 years). We also observe a modest increase in error by chronological age—healthy participants with chronological age less than 25 years are predicted with an MAE of 2.15 years (95% CI 1.95–2.34), while participants with chronological age between 65 and 75 years are predicted with an MAE of 3.21 years (95% CI 1.73–4.56). Prediction error in the general cohort is higher and more variable across all demographic groups. Figure 3e summarizes chronological age estimator error in demographic subpopulations. PpgAge residuals appear to be close to normal in the healthy test cohort with non-normality driven by a small number of outliers, and farther from normal in the general cohort, see Fig. S1.
PpgAge gap associates with disease
We investigate the hypothesis that an elevated predicted age relative to chronological age—i.e., the age gap—is associated with disease, and, inversely, a reduced (or negative) age gap is associated with better health. Using medical history surveys from participants at enrollment, we study age- and sex-matched diagnosis rates of a variety of conditions, stratified by PpgAge gap measured within the first 30 days of enrollment. We bin subjects by PpgAge gap (adjusted, see “Methods”) within discrete categories: <−2, (−2, 0], (0, 2], (2,4], (4,6], and >6 years.
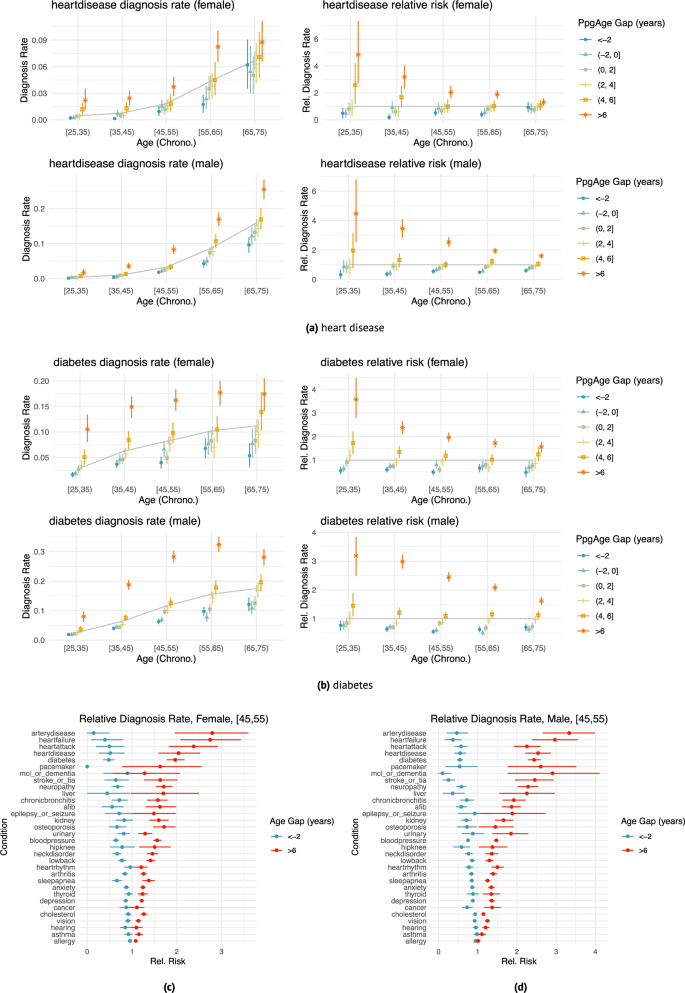
We observe a strong association between PpgAge gap and a variety of conditions, controlling for sex and chronological age (Fig. 4). Those with a higher (i.e., older looking) age gap tend to have higher diagnosis rates than average; those with lower (i.e., younger looking) age gap tend to have lower diagnosis rates. For example, the rate of diabetes diagnosis among 35–45 year old women is 6.3% (95% CI 5.7–6.8). However, for 35–45 year old women with a >6 year PpgAge gap, that rate jumps to 14.9% (95% CI 12.8–16.9), or 2.38 times the average rate (95% CI 2.10–2.70)—we refer to this ratio as the “relative rate of diagnosis” (see “Methods” for further details). For participants with a <−2 year gap, that rate drops 3.7% (95% CI 2.9–4.5), or a 0.59 relative rate of diagnosis (95% CI 0.47–0.71, Fig. 4b).
a, b Age- and sex-matched diagnosis rates (left) and risk relative to average (right) stratified by different age gap buckets for heart disease (n = 37,201 female and n = 63,345 male participants) and diabetes (n = 37,366 female and n = 63,571 male participants). Grey line indicates average diagnosis rate (by age and sex); all intervals are 95% confidence intervals computed with 1000 bootstrap samples. The effect size (relative to age- and sex-matched average) varies with age—e.g., heart disease diagnosis is less strongly associated with age gap in the [65, 75) year old group than the [35, 45) age group. Details for additional diseases are included in Supplemental Figs. S2 and S3. Heart disease diagnosis rates. c, d Age gap risk relative to average for all surveyed diseases; left: female participants aged 45–55 (n = 6,364), right: male participants aged 45–55 (n = 12,787), comparing oldest age gap bucket (>6) and youngest age gap bucket (<−2). Cardiometabolic diseases (e.g., heart failure, peripheral artery disease, diabetes) appear to have larger associations with age gap than other conditions (e.g., asthma, cancer, allergy). Intervals are 95% confidence intervals computed with 1,000 bootstrap replicates. See Fig. S13 for additional results.
As another example, among 35–45 year old male participants, a heart disease diagnosis is rare, reported at a rate of 1.0% (95% CI 0.9–1.2). However, among 35–45 year old male participants with >6 year PpgAge gap, the rate of heart disease diagnosis is 3.6% (95% CI 2.7–4.5), or 3.46 × the average (95% CI 2.80–4.10); and for those with <−2 year PpgAge gap, that rate drops to 0.4% (95% CI 0.2–0.6) or a 0.37 times the average rate (95% CI 0.19–0.56). Among 45–55 year old men, the relative rate of heart disease diagnosis for participants with >6 year PpgAge gap is 2.54 × (95% CI 2.22–2.87); for 45–55 year old men with a <−2 year gap, the relative rate is 0.55 × (95% CI 0.41–0.71, Fig. 4a).
This association is also strong for heart failure and peripheral artery disease (Fig. 4c)—in 45–55 year old men, those with a >6 year PpgAge gap have a 2.97 × (95% CI 2.39–3.56) relative rate of heart failure diagnosis; for 45–55 year old women the rate is 2.75 × (95% CI 2.08–3.43).
The association between PpgAge gap and diagnosis rates is not strong with all conditions. Allergy, asthma, vision loss, hearing loss, and cancer diagnosis rates remain similar in the youngest and oldest PpgAge groups. See Fig. 4 for a more detailed summary (and Figs. S2 and S3 for additional results).
PpgAge gap predicts incident cardiometabolic disease
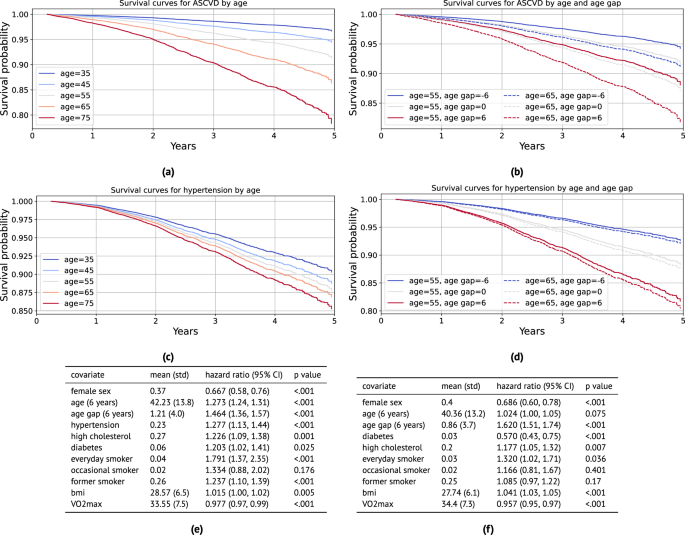
To better understand the utility of PpgAge age gap as a predictor, we conduct a survival analysis, predicting incident (i) atherosclerotic cardiovascular disease (ASCVD) events (new diagnosis of coronary artery disease, heart failure, or peripheral artery disease; or heart attack, stroke, angioplasty, stent, or coronary bypass; n = 1328 events), (ii) hypertension (n = 1449 events), (iii) hyperlipidemia (n = 1666 events), (iv) diabetes diagnosis (n = 1049 events); all while controlling for relevant risk factors.
For ASCVD events, we use the continuous-valued adjusted PpgAge gap, and control for biological sex, age, BMI, \({{{{\rm{VO}}}}}_{2}\,\max\), smoking status, and previous diagnoses of hypertension, high cholesterol, and diabetes. We find that a PpgAge gap of six years is associated with a significant risk increase, with a hazard ratio of 1.464 (1.36–1.57 95% CI). For context, a previous diagnosis of hypertension is associated with a hazard ratio of 1.277 (1.13–1.44 95% CI), and high cholesterol is associated with a hazard ratio of 1.226 (1.09–1.38 95% CI). Fitted survival curves from the Cox model for different ages and PpgAge gaps overlap, as well—the survival for a chronological 55 year old with a PpgAge gap of +6 is lower than for a chronological 65 year old with a PpgAge gap of −6.
We see a similarly strong association between a PpgAge gap of six years and risk for developing new hypertension, with a hazard ratio of 1.620 (1.51–1.74 95% CI). See Fig. 5 for full results on these conditions. For all conditions, we observe that an increase in PpgAge gap is a strong and statistically significant risk factor for onset of new disease, with the effect size for a gap of +6 being comparable to or occasionally greater than for other common risk factors like hypertension, smoking, or high cholesterol. In the general cohort, we note that PpgAge gap greater than 6 years constitutes 11.6% of participants (14,027 of 120,235), roughly the top decile. For comparison, the prevalence of hypertension, high cholesterol, diabetes, and heart disease diagnoses are 23%, 25%, 6.1%, and 2.3%, respectively.
a Fitted survival curves from the Cox model for incident atherosclerotic cardiovascular disease (ASCVD) for different ages. Average values for other covariates (except PpgAge gap) are used within each stratum (defined as ± 5 years). b Fitted survival curves from the Cox model for ASCVD stratified for 55 and 65 year old subjects, and further fixing PpgAge gap values, with other covariates set to average values within age strata. There is substantial overlap—55 year old subjects with high PpgAge gaps have lower survival to 65 year old subjects with low PpgAge gaps. c Fitted survival curves from the Cox model for incident hypertension diagnosis for different ages. Average values for other covariates (except PpgAge gap) are used within each age stratum (defined as ± 5 years). d Fitted survival curves from the Cox model for incident hypertension for 55 and 65 year old subjects, and further fixing PpgAge gap values, with other covariates set to average values within age strata. PpgAge is a much stronger predictor than chronological age, which has minimal effect. e Hazard ratios for the incident ASCVD Cox model, adjusting for common risk factors (C-index: 0.758, N: 89,553, number of events: 1328). f Hazard ratios for the incident hypertension Cox model, adjusting for common risk factors (C-index: 0.704, N: 70,636, number of events: 1449). P-values reflect a two-sided Wald test, unadjusted for multiple comparisons. See Supplemental Fig. S4 for additional results on incident diabetes and hyperlipidemia, Fig. S5 for young vs old subgroup analyses, and Fig. S6 for Kaplan–Meier curves with confidence intervals stratified by PpgAge gap. As we are not modeling repeated or competing events, cumulative incidence is equivalent to the inverse of the survival probability, CIF(t) = 1 – S(t).
In Fig. S5 in the supplement, we detail a sensitivity analysis that yields similarly strong associations between PpgAge gap and incident disease when we fit models within older and younger subgroups. In Fig. S6, we also show Kaplan–Meier curves for each of the outcomes stratified by PpgAge gap, where we observe statistically significant increases in risk for all conditions for subjects with the highest PpgAge gap.
PpgAge predictions associate with smoking behavior
Participants in AHMS are surveyed about behaviors related to health, including smoking status. Individuals are asked, “Have you smoked at least 100 cigarettes in your entire life?”, and if the response is “yes” or “do not know,” participants are asked, “Do you now smoke cigarettes every day, some days, or not at all?” We categorize individuals into never smokers (n = 58,025), former smokers (n = 25,644), occasional smokers (n = 2453), or daily smokers (n = 4190) based on available survey responses, and study the age gap of each group (see “Methods”).
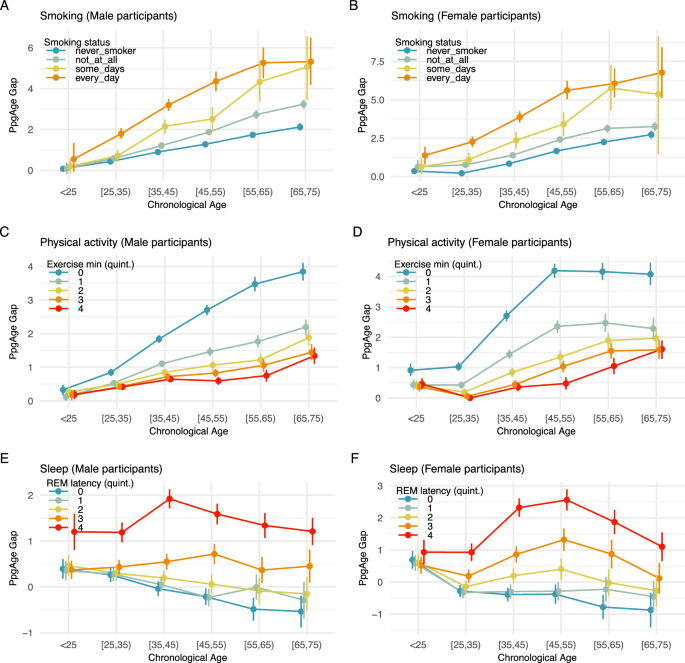
More frequent smoking is consistent with a higher PpgAge gap. Across all age groups, and for both male and female participants, daily smoking is associated with the highest age gap, followed by occasional smokers, former smokers, and then never smokers. Additionally, the age gap difference across smoking categories grows from the youngest to oldest chronological age categories. Among males younger than 25 years, the predicted age gap for daily smokers, 0.55 years (95% CI −0.06–1.343), is similar to the predicted age gap for never smokers, 0.076 (95% CI −0.01–1.7). However, older populations deviate markedly—among 25–35 year old males, the predicted age gap for daily smokers is 1.36 years higher than for never smokers (1.79 vs 0.43); that difference increases to 2.3 years in the 35–45 group (3.2 vs 0.89), and 3.53 years in the 55–65 group (5.27 vs 1.74). See Fig. 6A, B for additional details.
PpgAge gap (adjusted) stratified by self-reported smoking status and chronological age for A male and B female participants. Results in both subpopulations are consistent with a dose-response effect—never smokers (n = 58,025) appear younger than former smokers (n = 25,644), who appear younger than occasional smokers (n = 2453), who appear younger than daily smokers (n = 4190). In both populations, results are also consistent with an exposure effect—i.e., the gap between daily smokers and never smokers is small in the youngest population, but grows to be about 3–4 years in the [55,65) year old groups. PpgAge gap stratified by C male (n = 98,986) and D female (n = 54,256) participants, stratified by exercise minutes. Among men, the age gap is largest for the lowest exercise minutes quintile, i.e., the least active individuals, and the difference between the lowest and the remaining quintiles grows with age, consistent with an exposure effect. The ranking of the average age gap is consistent with increasing amounts of exercise minutes. Among women, a similar effect can be observed, although the uncertainty is slightly larger due to a smaller sample size. (See quintile cutoffs in Table S1.) E, F PpgAge gap by REM latency quintile for male (n = 56,802) and female (n = 32,769) participants, respectively. An increased REM latency is associated with an elevated PpgAge gap across all age categories. See Fig. S10 for analysis of total sleep duration, deep sleep duration, and sleep efficiency. All intervals are 95% confidence intervals about the mean from 1000 bootstrap replicates.
PpgAge predictions associate with exercise behavior
The Activity app on Apple Watch estimates physical activity level, including daily “exercise minutes,” the time spent on a “brisk activity” (defined as an activity at or above a brisk walk38), or a logged workout44. For each participant in the general cohort, we compute average daily exercise minutes over the course of study enrollment, and categorize men (n = 98,986) and women (n = 54,256) into five groups based on quintiles of the (age- and sex-matched) average exercise minutes distribution. We then study the age gap in relation to this activity variable and age.
For both male and female participants and across age categories, higher daily exercise minutes is consistent with a smaller age gap, see Fig. 6C, D. Similar to the smoking result above, we observe an increase in the age gap across exercise groups from the youngest cohort to the oldest. Individuals younger than 25 years old have mostly similar average age gaps across all quintiles of exercise minutes, with the exception of female participants in the lowest exercise minutes quintile (i.e., the least active individuals). For this group, the average age gap already deviates upwards from the remaining quintiles. For older age groups, individuals in the lowest exercise minutes quintile have an average age gap that deviates more and more from individuals in the higher exercise minutes quintiles. For example, for men younger than 25 years, the average age gap is 0.33 years (95% CI 0.17–0.48) in the lowest quintile vs 0.19 years (95% CI 0.06–0.33) in the highest quintile. For men between 35 and 45 years, individuals in the lowest quintile have an average age gap of 1.84 years (95% CI 1.73–1.95) vs 0.65 years (95% CI 0.56–0.74) for the highest quintile. Finally, for men between 65 and 75 years, the least active individuals have an average age gap of 3.85 years (95% CI 3.58–4.11) vs 1.34 years (95% CI 1.11–1.58) for the highest quintile. For women, we observe similar effects, although the uncertainty is slightly larger due to the smaller sample size. Finally, the ranking of the average age gap is consistent with increasing amounts of exercise minutes. See Fig. 6C, D for additional details, and Section S2 and Figs. S8 and S9 for additional summaries of activity and fitness.
PpgAge gap associates with disease rates when controlling for cardiorespiratory fitness
We also compare diagnosis rates within age-, sex-, and \({{{{\rm{VO}}}}}_{2}\,\max\)-matched groups using a subset of participants that have a \({{{{\rm{VO}}}}}_{2}\,\max\) estimate (n = 89,062). We find that the association observed for age- and sex-matched categories remains when controlling for \({{{{\rm{VO}}}}}_{2}\,\max\). For example, for women 45–55 years old, even among the most fit (highest \({{{{\rm{VO}}}}}_{2}\,\max\)) quintile, the oldest looking (q4) participants have a 2.1 times higher rate of high blood pressure diagnosis—a figure that was more in line with the average diagnosis rate of the second lowest \({{{{\rm{VO}}}}}_{2}\,\max\) category. See Fig. S9 for comparisons.
PpgAge gap associates with sleep stages
A subset of participants in AHMS contribute sleep stage data collected by Apple Watch45 (n = 56,802 men and n = 32,769 women). Sleep stages are categorized as “Awake,” “Deep,” “Core,” and “REM,” in the Health app and are derived from an accelerometer-based algorithm45. We study the association between PpgAge and several sleep-related variables, controlling for demographic factors.
For each available participant night (n = 16,093,920), we extract 4 sleep-related variables, (i) total sleep duration, the total time spent in non-"Awake” stages, (ii) deep sleep duration, the total time spent in the “Deep” stage, (iii) sleep efficiency, the total sleep duration divided by the elapsed time from the onset of first non-"Awake” stage to the end of the final non-"Awake” stage, and (iv) REM latency, the time from the onset of first non-"Awake” stage to the onset of first “REM” stage. Similar to smoking and exercise, we investigate the association of age gap with these sleep-related variables across age- and sex-matched groups. For further validation, we fit ordinary least squares (OLS) model for age-matched groups as well as the entire population, where the target variable is the age gap and explanatory variables include chronological age, biological sex, BMI, and the four sleep-related variables (see “Methods” for additional details).
We observe that across age- and sex-matched groups, earlier REM latency, longer total sleep duration, longer deep sleep duration, and higher sleep efficiency, are consistent with lower age gap, see Figs. 6E, F and S10a–f. Consistently, we observe similar association effects in the sign of the coefficients in OLS models, see Fig. S10g, h. First, the sign of the coefficients for total sleep duration, deep sleep duration and sleep efficiency are negative and consistent across different age-matched groups, indicating that longer total sleep duration, longer deep sleep duration and higher sleep efficiency associate with negative age gap (i.e., younger-looking status). Second, the sign of the coefficient for REM latency is positive across different age-matched groups, indicating that earlier REM latency associates with negative age gap (i.e., younger-looking). Figure S10h contains the statistics from the OLS models, indicating that all coefficients are significant. Interpreting efffect sizes, one additional hour of total sleep associates with 0.09 years of reduced age gap, and one additional hour of deep sleep associates with 0.99 years of reduced age gap. One extra percentage of sleep efficiency associates with 0.05 reduced age gap, and one hour earlier REM latency associates with 0.47 reduced age gap.
PpgAge predictions use morphological features beyond heart rate and heart rate variability
HR and HRV are common summaries of cardiac rate and rhythm estimated from PPG segments. HRV is known to decline with age and decreased health, and rise with increased aerobic fitness46. The full PPG waveform reflects changes in blood volume in the microvascular bed of tissue31, which may contain subtle-yet-informative patterns relevant to aging (see Fig. S11. To investigate this information difference, we compare PpgAge predictions (i.e., using the full PPG waveform via the learned representation) to models that only use HR and HRV as inputs.
Using the same training subjects and segments, we compute the 30-day mean, standard deviation, minimum, and maximum of HR and a set of HRV metrics (see S3 for full details), and use as features in both a linear model and a random forest model. HR/HRV-based models predict age less accurately than PpgAge across all subpopulations. In the healthy cohort, the linear and random forest model predict age with MAE of 6.10 years (95% CI 5.87–6.33) and 6.14 years (95% CI 5.91–6.37), respectively, significantly worse than the PpgAge predictions on the same test subjects, 2.42 years (95% CI 2.30–2.54). See Fig. S12 for additional details and comparisons to HR/HRV models.
PpgAge predictions are consistent with known features of aging
To shed light on what features PpgAge uses, we visualize segmented PPG beats that correspond to high and low age gaps across a range of chronological age groups in Supplemental Fig. S11. The age gap is picking up on the typical features of aging (see Charlton et al.29 Fig. 4), i.e., the dicrotic notch and diastolic peak disappear as an individual appears older across all chronological age groups. While these features appear to be important to our prediction (and are not captured by HR/HRV metrics), it is possible that predictions exploit more subtle, data-driven features with unknown physiological roots.
Modeling healthy aging strengthens association between age gap and disease
Additionally, training the PpgAge model on a healthy cohort induces a stronger association between the age gap and diagnosis rates compared to a model trained on a randomly selected (i.e., representative) cohort of equal size. Among 35–45 year old men, a PpgAge gap >6 years based on the model trained on the healthy cohort has a relative rate of diabetes diagnosis of 2.99 × the average (95% CI 2.74–3.23); when training on a random subset, this relative diagnosis rate drops to 2.18 × (95% CI 1.89–2.46). Differences between the two models are more pronounced in older groups. Among 65–75 year old men, a PpgAge gap >6 years from the healthy-trained model carries a 1.61 × relative diabetes diagnosis rate (95% CI 1.47–1.75); the general-trained model has a relative rate of 1.1 × (95% CI 0.97–1.23)—that is, the general model age gap does not stratify older male subjects into high and low prevalence groups at all. See Supplemental Fig. S13 for a more details.
Compared to PpgAge HR/HRV-based age gaps weakly associate with disease
We again compare age gap associations using the full PPG model to models trained using only HR/HRV features. In general, we see a much weaker association with self-reported diagnoses than the full waveform model. As an example, for 45–55 year old men, the relative rate of diabetes diagnosis in the oldest looking quintile is 2.1 (95% CI 1.96–2.20) with PpgAge (i.e., using the full waveform). That drops to 1.25 (95% CI 1.15–1.35) when using the HR/HRV-based random forest model. For peripheral artery disease in that same group, the comparison is 2.8 (95% CI 2.32–3.26) for the full waveform model, which drops to 1.47 (95% CI 1.044–1.90) for the HR/HRV model. This weakened association suggests that HR and HRV alone convey some information about disease in the PPG signal, while the full waveform morphology contains richer information. Notably, we see either no change or improvement for prevalence of pacemaker, suggesting HR/HRV information is a sufficient correlate of the condition. See Figs. S12 and S11 for more details.
Longitudinal PpgAge associates with pregnancy status
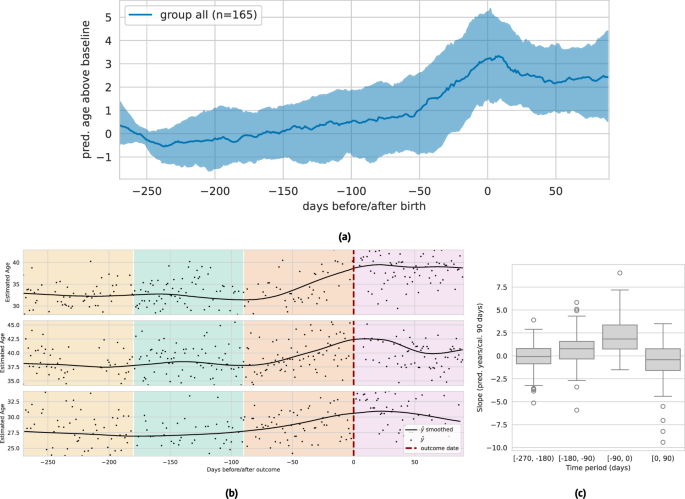
Recent work has shown that pregnancy is associated with accelerated biological aging as measured by epigenetic biomarkers47,48. Here, we examine the relationship between PpgAge and pregnancy on a subset of participants in AHMS who become pregnant during the study. We subset to participants who self-report no pregnancy at baseline and report either a vaginal birth or Cesarean section in a monthly health update survey (n = 690). We further subset to participants with sufficient age estimates proximal to the date of the reported pregnancy outcome—at least 20 days of age estimates in three 3-month periods before and one 3-month period after parturition (n = 165).
In the 270 days preceding birth, we observe a steady median increase leading into a sharp median increase around 60 days before parturition, where PpgAge peaks and then slowly declines. Over this (approximate) pregnancy period, we observe a median increase of 3.56 years (IQR 1.65–5.65). Additionally, we observe a significantly larger slope in the three month period directly preceding birth, and a negative median slope in the 90-day period following pregnancy. We note this increase in PpgAge over the pregnancy period is in line with increases estimated with DNA methylation biomarkers47; see Fig. 7 for visual and statistical summaries. A longer observation window is required to assess how persistent this effect is, or if PpgAge reverts to pre-pregnancy levels. On a smaller subset with sufficient longitudinal data (n = 29), we observe a slightly negative median age gap slope for a year post parturition; see Fig. S14 for more details and subpopulation comparisons by age, BMI, and pregnancy complications.
a Median (black) and interquartile range (gray) of lowess-smoothed predicted age time series (centered around predicted age during first 90 days of approximate pregnancy period), n = 165 participants. We observe a median 3.56 year [1.65–5.65 IQR] increase in predicted age throughout the pregnancy period, peaking at time of birth. Estimate age increase is similar to those reported in epigenetic age biomarkers47. b Examples of longitudinal predicted age with parturition date (i.e., vaginal delivery or Cesarean section) highlighted, with background colors denoting the three 90-day periods before, and one 90-day period after. We subset to individuals in the study that (i) report not pregnant at study start, (ii) report a pregnancy outcome, and (iii) have at least 20 days with predicted age available in each of the three month periods (n = 161). c The distribution of slopes within each of these 90-day periods (n = 165). We observe a significantly higher slope in the period immediately preceding birth, and a slight negative slope in the period immediately following birth. The box depicts quartiles of the data, with the whiskers 1.5 times the inter-quartile range from the first and third quartiles. See Fig. S14 for additional analysis.
PpgAge often increases around certain major adverse cardiovascular events
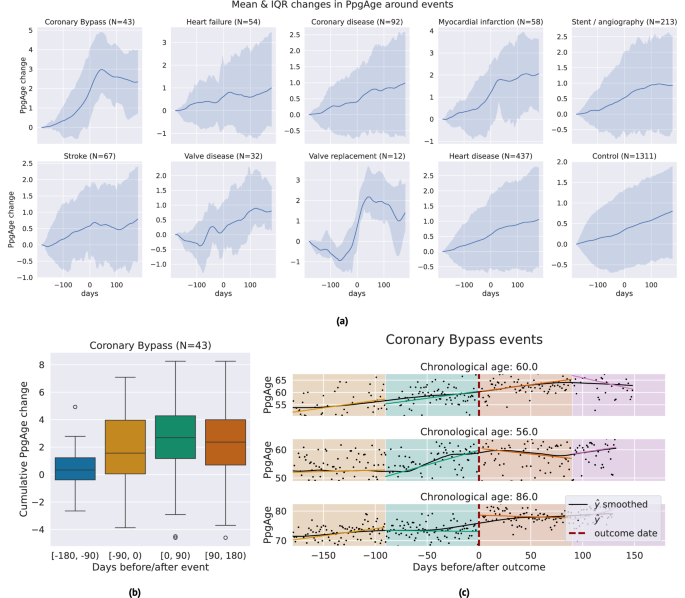
We investigate the sensitivity of participant-level PpgAge time series to cardiac events. Centering the self-reported event date at time 0, we examine the time period of 180 days before to 180 days after, and visualize the median and interquartile range of lowess-smoothed PpgAge time series. For coronary artery bypass graft (CABG) surgery, mycoardial infarction events, and valve replacement surgery, we see median predicted age increases from 1.7 to 2.5 years. Investigating individual time series for subjects with a CABG (Fig. 8), we see variability from participant-to-participant. Some participants exhibit a sharp changepoint at the time of the event, while others exhibit more gradual increases PpgAge time series. Additional time series and distributions of the cumulative change in PpgAge for myocardial infarction and valve replacement can be found in Fig. S7.
a Median (blue line) and interquartile range (shaded blue) of lowess-smoothed PpgAge time series, normalized to 0 at 180 days before the date of the event. Each subplot shows how PpgAge estimates change before and after cardiac events of different types, as well as for non-event controls (bottom right subplot). For bypass surgery, myocardial infarction, and valve replacement surgery, we see median increases of around 2 years over the one year time period. b Distribution of cumulative PpgAge increase from −180 days before to +180 days after a coronary bypass surgery, within each 90-day period, n = 43 participants. The box depicts quartiles of the data, with the whiskers 1.5 times the inter-quartile range from the first and third quartiles. c Individual examples of predicted age trajectories, centered on a coronary bypass event. Individual examples reveal heterogeneity of predicted age sensitivity–some exhibit a strong change point around the event, while others continue current trajectory. A randomized control study complementing this can provide insights into potential confounders.
Discussion
We propose PpgAge, a wearable-based biomarker that is easy to collect, highly predictive of healthy aging, strongly associated with a variety of age-related conditions, predictive of incident disease, and sensitive to some longitudinal physiological changes. Within the biological aging literature, this work is a unique combination of data modality and study scope—wrist PPG from a consumer wearable and evidence from hundreds of thousands of participants with over 149 million participant-days in a naturalistic setting, with some contributing up to 4 years of longitudinal data. Such an easy-to-collect aging clock has the potential to shed light on interventions and clinical decisions at much finer time scales than existing age clocks. PpgAge could be a more granular lens in the study of human longevity, the monitoring of patient health, and the assessment of new treatments.
Moqri et al.13 delineate four desiderata for a biomarker of aging to support human longevity research—such a biomarker should be (i) minimally invasive and reliable (i.e., longitudinal measurements are feasible), (ii) relevant to age, (iii) predictive of functional aspects of aging (e.g., disease and decline) better than age alone, and (iv) responsive to longevity interventions. The proposed PpgAge addresses each.
The size and scope of AHMS itself establishes that PpgAge is minimally invasive and reliably measurable. The use of signals from a popular consumer wearable indicates the potential scalability of our approach.
We show that PpgAge accurately predicts chronological age—achieving an MAE of about 2.4 years for healthy subjects and 3.2 years for the general cohort (Fig. 3). This accuracy compares favorably to studies of other aging biomarkers, including ECG (e.g., MAE 6.9–8.4 years22,23), labs and vitals (e.g., MAE 3.7–4.5 years28), EEG (e.g., MAE 7.6 years25), PSGs (e.g., MAE 5.8 years24), and retinal imaging (e.g., MAE 2.86–3.30 years7). We also demonstrate that PpgAge is accurate across demographic subpopulations, including biological sex, race/ethnicity, and BMI (Fig. 3e). Further, PpgAge remains accurate despite a strong distribution shift; though trained on healthy participants, PpgAge produces accurate predictions on the general study population.
Our analysis also shows that PpgAge is associated with diseases and behaviors linked to age-related decline. The PpgAge gap statistic stratifies participants into low and high prevalence groups for a variety of conditions, including heart disease, heart failure, diabetes, liver disease, peripheral artery disease, among others. This stratification persists even when adjusting for age, sex, and cardiorespiratory fitness as measured by estimated \({{{{\rm{VO}}}}}_{2}\,\max\) (Fig. S9).
PpgAge gap is also a significant predictor of incident heart disease events and diabetes diagnoses (Fig. 5), even when controlling for relevant risk factors. For predicting new heart disease events, a PpgAge gap of 6 years had a similar effect size as a previous diagnosis of high cholesterol, and a stronger effect than a previous diagnosis of hypertension or diabetes. For both new heart disease events and new diabetes diagnoses, PpgAge gap is a significant predictor even when controlling for relevant risk factors.
PpgAge exhibits a strong association with smoking status, exercise, and sleep—behaviors strongly linked to health and longevity. For both smoking and exercise, we observe a PpgAge gap pattern consistent with a dose-response and an exposure effect. More frequent smokers are predicted to be older across age groups, and the age gap between smoking categories grows larger in older participants, consistent with a cumulative effect of smoking on PpgAge (Fig. 6A, B). Similarly, increased physical activity is associated with a lower age gap, and the PpgAge delta between sedentary and active participants is wider in older participants (Fig. 6C, D). PpgAge is also correlated with standard measures of sleep quality—while reduced sleep duration is consistent with an increase in average PpgAge, reduced deep sleep duration, increased REM latency, and decreased sleep efficiency are associated with larger increases in predicted age (Figs. 6E, F and S10). Though suggestive, our evidence is from an observational cohort, and these behavioral associations do not establish a causal dose-response or exposure effect. Our analysis does not, however, preclude the possibility that PpgAge is modifiable and meaningfully responsive to changes in behavior that promote longevity. A more controlled comparison (e.g., involving a detailed history of smoking and exercise behavior and randomization) is necessary to make stronger claims.
We also find that PpgAge is longitudinally sensitive to concurrent physiological changes. Pregnancy is associated with a rapid increase in predicted age, with a median of about 3.5 years (Fig. 7). This rapid increase is consistent with DNA methylation-based age biomarkers, which found that maternal biological age increased by 2.39 years for PCPhenoAge (95% CI 1.75–3.03), 1.19 years for PCGrimAge (95% CI 0.93–1.46), 2.52 years for GrimAge2 (95% CI 2.09–2.95) during pregnancy47. However, unlike these epigenetic biomarkers, PpgAge does not appear to rapidly normalize, but decreases slowly following parturition. A longer observation window and further study is needed to assess to what degree this increase in PpgAge persists or return to baseline. Additionally, we see large predicted increases surrounding reported cardiac events, including bypass surgery, non-ST-elevation myocardial infarction, ST-elevation myocardial infraction, and valve replacement surgery. Some individuals exhibit a sharp, sudden increase, while others continue an existing trend (Fig. 8).
With ease of measurement, scalability, strong association with chronic disease, health-related behaviors, and apparent longitudinal sensitivity to physiological changes, PpgAge is a promising candidate to assess the efficacy of longevity interventions, addressing the desiderata of Moqri et al.13. And relative to other wearable data, a core benefit of PPG at rest is that the signal isolates cardiovascular function from behavioral changes, reflecting not transient changes in user behavior, but their physiology.
Beyond potential uses in longevity research, PpgAge has the potential for clinical translation. The survival analysis (summarized in Fig. 5) shows that PpgAge gap is predictive of incident disease diagnoses and adverse cardiovascular events when controlling for relevant risk factors, motivating further study into PpgAge gap’s incorporation into cardiovascular disease risk scores. The strong association between chronic disease history and elevated PpgAge gap suggest that it may provide complementary information for clinical decisions that otherwise would be based solely on chronological age, e.g., screening and triggering additional clinical tests. PpgAge may also be useful for monitoring individuals outside the clinic, as it may convey signs of worsening disease (e.g., heart failure) or sudden, unexpected changes.
We also show that reducing the full PPG waveform to a coarser summary (e.g., HR and HRV) significantly reduces prediction accuracy and association with health conditions (Fig. S12). PPG morphology, as here exploited, is known to vary in age-dependent ways as arteries stiffen, myocardium thickens, and cardiac output wanes—and morphological features are unavailable when only considering rhythmic summaries.
Additionally, we find that a model fit to only healthy subjects strengthens the association of PpgAge gap with disease, suggesting that such cohort selection better captures correlates of the healthy aging process than a random subsample of participants. While it has been established that more precise age predictions may reduce the association of the gap to age-related disease or mortality (with the extreme of perfect age estimates as being no better than age itself, trivially)49, there is also evidence that selecting participants to learn a normative aging model—i.e., by training a model on only healthy participants—can produce an aging clock that is predictive of overall mortality28.
We study this phenomenon by directly comparing a normative aging model (i.e., trained only on healthy participants) to a general aging model (i.e., trained on a random subset of participants). And similarly, we found that while age estimates are slightly more precise on the general cohort when training on a random subset (as expected, since there is no distribution shift), the age gap association with disease diagnosis is weaker across nearly all diseases in all age/sex groups (see Supplementary Fig. S13). This result is consistent with the prevailing understanding—predicting chronological age without considering information about participant health yields a less useful age clock. An advantage of this approach is that we are able to use the more widely available chronological age and survey information, as opposed to more direct measurements of arterial stiffness (e.g., carotid-femoral pulse wave velocity or brachial-ankle pulse wave velocity) or risk scores of cardiovascular disease (e.g., Framingham or ASCVD scores) as a vascular age reference50.
There are several limitations to our study. The use of naturalistic (i.e., observational) data is both a strength—scalability and simplicity—and a limitation. The participants in the AHMS may not be representative of the general population, complicating the generality of our findings. Further, our association study is based on patient self-report, which may include unreliable or missing responses. (Though, we note that under-reported previous diagnoses would weaken the apparent association between age gap and disease.) Complementing this observational study with smaller, randomized studies would strengthen the evidence for PpgAge to act as a useful biomarker for assessing longevity interventions and augmenting clinical decisions51. And though AHMS represents a geographically diverse population across the United States, our analysis and conclusions are currently limited to this one study. In future work, we aim to validate both age predictions and PpgAge gap associations with disease on additional studies.
Despite the size and duration of AHMS, the time series of PpgAge measurements is at most four years for any one participant (at the time of this study). The development of age-related disease and decline often occurs on much larger timescales. We would need to observe an even longer time period to assess the sensitivity of PpgAge to the development of disease and to the response to some behavioral interventions. Further, our study does not have mortality information, an important endpoint to study. And though we investigate the association between PpgAge gap and sleep, we do not investigate its relationship to chronotype. A strong association between shift work and metabolic disease has been established52,53, and it is an open question if our metric correlates with such disruption of a regular sleep schedule.
Although we observe evidence of longitudinal sensitivity within participants, we note that the rate of change of PpgAge appears to be calibrated differently between age groups (see Fig. S1d). Younger healthy participants have a PpgAge rate of change closer to one; older healthy participants have a reduced PpgAge rate, which may be due to a healthy sample that is skewed younger. To properly calibrate PpgAge age changes for all age groups, a statistical model that incorporates temporal dynamics, subject-level groupings, and heterogeneity across age groups is likely needed. If PpgAge rates remain persistently differently calibrated, downstream uses cases (e.g., risk stratification) would need to incorporate age-specific effects on PpgAge gap.
We also employ a relatively conservative definition of “healthy” when constructing our aging model. For example, we observe very few individuals above 75 years of age who meet our three criteria (no disease, no medications, no smoking history), suggesting that our statistical model does not “see” examples of healthy aging beyond the age of 75. Potentially a more relaxed (or even age-adapted) definition of “healthy” would induce a more informative predicted age in the older population.
Further, we have a limited understanding of the underlying physical mechanisms that drive age predictions. Based on our understanding of the PPG sensor, it is possible that the model is identifies signatures of cardiovascular-related aging, e.g., arterial stiffening and reduced cardiac output, and more general vascular health. Association with other categories of disease or physiological state, e.g., sleep and pregnancy, maybe driven by an underlying correlation with cardiovascular function. A better understanding of the physiological mechanisms underlying these predictions could lead to a more robust and interpretable biomarker of aging. Such physiological insights could also shed light on potentially effective longevity interventions or incorporated into a more holistic, heterogeneous model of aging (e.g., refs. 28,54).
Despite these limitations, our study demonstrates that a wearable-based digital biomarker of age may be useful in the study of human longevity, with the potential for clinical translation.
Methods
Data collection
Our study uses data from the AHMS, an ongoing research study that started on November 14, 2019, conducted in partnership with the American Heart Association and Brigham and Women’s Hospital. AHMS was designed to examine connections between physical activity and cardiovascular health. Study participants were all Apple Watch users, at least 18 years of age (at least 19 years old in Alabama and Nebraska; at least 21 years old in Puerto Rico), who resided in the United States and provided informed consent electronically in the Apple Research app. The study was approved by the Advarra Central Institutional Review Board and registered to ClinicalTrials.gov (ClinicalTrials.gov Identifier: NCT04198194)41. The Apple Research app collected all data, both raw measurements and metadata.
As mentioned above, Apple Watch intermittently and passively records green (525 nm) 60-s PPG signals during low-motion periods throughout the day using light-emitting and light-sensitive diodes. Participants were included in this study based on availability of background PPG segments and surveys. Due to comparatively small numbers of individuals self-reporting ethnicity of “American Indian or Alaskan Native,” “Middle Eastern or North African,” “Native Hawaiian or other Pacific Islander,” and “None of these fully describes me,” these subjects were combined into a single race/ethnicity group ("Other”) when used for downstream subgroup and stratified analysis; subjects who self report multiple race/ethnicity categories are assigned a single group ("Multi”). Body mass index was determined from self-reported height and weight at study start. For privacy, subjects report only birth year, not date; we approximate chronological age by assuming a July 1st birthday within the self-reported birth year.
Upon entering the study, participants are surveyed about their medical history, asked, “Have you ever been diagnosed with any of the following conditions?” with the possible responses of “Yes,” “No,” “I don’t know,” and “I prefer not to answer.” A full list of conditions can be found in the Supplement. Participants are also asked, “Do you currently take any medications?” Additionally, participants are surveyed about health behaviors, including smoking status and frequency. Participants are also periodically asked about health updates. These questions include updates about new diagnoses, new medications, and pregnancy event outcomes, among others. Responses to these surveys are used to study the association between predicted age, disease, and behavior. See Supplemental Section S1 for further detail.
Data processing, representation learning, and modeling
Our modeling framework consists of three steps: (i) PPG preprocessing; (ii) pre-training a general-purpose encoder via SSL on unlabeled PPG data from AHMS; and (iii) learning a linear prediction head, i.e., linear probing, from the pre-trained encoder to age as target variable.
Passively recorded green PPG signals are sampled at 64 Hz or 256 Hz, and consist of four separate optical channels corresponding to different spatial combinations of transmitting and receiving diodes. Signals are collected from a variety of watch models and OS versions (see Supplemental Fig. S15). All 60-s PPG measurements used in this analysis used the same mode of sensor operation, across all Watch models and OS versions represented in the data set. We pre-processed PPG segments using dark subtraction (to reject signal introduced by ambient light), followed by bandpass filtering, down-sampling to 64 Hz (if needed) and temporal channel-wise z-scoring. See Abbaspourazad et al.42 for further PPG pre-processing details. We also only consider PPG segments that meet a quality threshold—that a beat segmentation algorithm is able to find beats that cover at least 90% of the segment. Other quality metrics may be suitable, such as limiting the accelerometer magnitude over the entire segment.
SSL has been proven successful in various domains of deep learning leading to state-of-the-art general-purpose models in natural language processing55,56, computer vision57,58,59, speech recognition60,61, and health42. These general-purpose models, also known as foundation models, are typically large neural networks that are pre-trained on a large volume of unlabeled data and are shown to contain information for a wide array of downstream targets. We pre-trained our PPG foundation model using 19,993,427 PPG segments from 172,318 participants in AHMS. Our PPG foundation model is a neural network that maps a 4-channel green PPG signal into a 256-dimensional feature vector called representation. Pre-training implementation and details remain the same as Abbaspourazad et al.42, where it was shown that PPG foundation models encode significant demographic and health-related information. Though almost all available participants are incorporated in this SSL preprocessing step, crucially no information about disease or chronological age is used.
Following Tian et al.28, we construct a normative age model by first selecting adults who self-report no disease, no medications, and no history of smoking at study start (see Supplemental Section S1 and Fig. S16 for further details), keeping only those with at least 30 PPG measurements within the first 30 days of the study, which results in 6728 participants. We divide this cohort into two sets at random—the healthy train cohort (5355 participants, ~ 80%) and the healthy test cohort (1373 participants, ~ 20%). We fit a linear model with a ridge penalty that takes the average PPG representation from the first month of study and predicts chronological age using participants in the healthy train cohort. The strength of the regularization is tuned using fivefold cross validation; performance is not particularly sensitive to regularization. We refer to subjects not in the “healthy” cohort as the “general” cohort (n = 120,235), all of whom are held out test participants. See Fig. 2b, c for cohort summary statistics and healthy cohort inclusion.
For each participant in the study, we use a subsample of the first month (and last month) of PPG segments to form an age estimate. The raw PpgAge gap is defined to be the difference between the estimated age and the true age, \(\hat{y}-{y}_{true}\), to form the baseline age gap—a higher value indicates that the participant “appears older,” and a lower value indicates that the participant “appears younger.” Following Smith et al.62 and Tian et al.28, we adjust the PpgAge gap statistic to remove any age dependence using a second step correction model. To do so, we regress the raw PpgAge gap on chronological age itself using a spline model, retaining the residual of this stage as the adjusted PpgAge gap.
Statistical analyses and reproducibility
Due to our large sample size, we conduct a non-parametric analysis of (chronological) age- and sex-matched cohorts; no statistical method was used to predetermine sample size. All results reported in this study use participants who were not included in model fitting (i.e., held out test subjects). Each analysis includes a subset of participants with the appropriate data (e.g., survey response, BMI measurement, etc). All error bars reported are 95% confidence intervals computed with 1000 bootstrap replicates. We define age bins to be ages into <25, 25–35, 35–45, 45–55, 55–65, 65–75 categories (left inclusive) and consider self-reported male and female biological sex groups. In analyses that include body mass index (BMI), following CDC guidance, we bin participants into groups corresponding to underweight (<18.5 kg/m2), healthy weight ([18.5–25) kg/m2), overweight ([25.0–30) kg/m2), and obese (>30 kg/m2), calculated using self reported weight and height63.
Diagnosis rates
For each group (e.g., 25–35 year old men), and condition (e.g., “diabetes”), we compute an average diagnosis rate by only considering participants with the responses “Yes” and “No” to the survey question. Concretely, for age group a, biological sex s, and condition c, the average rate is
$${\mu}_{a,s,c}=\frac{\{\#\,{{\hbox{``}}{{{\rm{yes}}}}{\hbox{''}}}\}_{a,s,c}}{\{\#\,{{\hbox{``}}{{{\rm{yes}}}}{\hbox{''}} \,{{{\rm{or}}}}\, {\hbox{``}}{{{\rm{no}}}}{\hbox{''}}}\}_{a,s,c}},$$
(1)
excluding participants with missing responses. Within each group defined by a, s, c, we stratify participants into buckets based on their age gap \(\hat{y}-y\), e.g., a “youngest looking” subgroup with an age gap <−2 and an “oldest looking” subgroup with an age gap >6 years. Within each bucket q, we compute the diagnosis rate
$${\mu}_{a,s,c,q}=\frac{\{\#\,{\hbox{``}}{{{\rm{yes}}}}{\hbox{''}}\}_{a,s,c,q}}{\{\#\,{\hbox{``}}{{{\rm{yes}}}}{\hbox{''}}\,{{{\rm{or}}}}\,{\hbox{``}}{{{\rm{no}}}}{\hbox{''}}\}_{a,s,c,q}}.$$
(2)
Within each group, we also compute the “risk relative to average,” which is simply the ratio
$${R}_{a,s,c,q}=\frac{{\mu }_{a,s,c,q}}{{\mu }_{a,s,c}}.$$
(3)
Incident disease survival analyses
To assess PpgAge gap’s association with incident disease, we use Cox regression models. We analyze four outcomes: (i) new atherosclerotic cardiovascular disease (ASCVD) events, (ii) new hypertension events, (iii) new diabetes diagnosis events, and (iv) new hyperlipidemia events. For all outcomes, we control for biological sex, chronological age, smoking status, BMI, and \({{{{\rm{VO}}}}}_{2}\,\max\). For ASCVD, we additionally control for previous diabetes, hypertension, and hyperlipidemia diagnosis. For hypertension, we control for previous diabetes and high cholesterol. For hyperlipidemia, we control for previous diabetes and hypertension. For diabetes, we control for previous high cholesterol and hypertension.
For each outcome, we study the effect associated with (adjusted) PpgAge gap at baseline, by taking the average value within the first 90 days of the study. We limit to subjects who self-report not having the condition in question from the medical history survey taken at baseline. Other historical diagnoses are also determined by the baseline medical history survey. All outcome information is obtained from quarterly/monthly health surveys, where participants are asked about updates to their medical history (specifically new diagnoses or major medical events). The new ASCVD event is a composite endpoint of a new diagnosis of coronary artery disease, heart failure, or peripheral artery disease; or a new heart attack, stroke, angioplasty, stent, angiography, or coronary bypass. For non-event subjects, we define their censoring date to be their last followup survey date before a gap in survey coverage of 90 days or more (e.g., if a subject stopped taking the followup surveys 1 year after enrollment and resumed again at year 3, their censoring date would be 1 year). We also remove any subjects who have an event or censoring date within the first 90 days of the study.
For each outcome in results tables in Figs. 5 and S4, we display the mean (and standard deviation, for continuous values) of the covariate (i.e., biological sex, chronological age, etc), the associated hazard ratio (and 95% CI), and the calculated p-value. Though the model was fit using a continuous-valued age gap, hazard ratios for chronological age and PpgAge gap are scaled to be in units of 6 years for reporting, while all other variables are on their original scales. Each Cox regression was fit with the lifelines Python package. The survival curves shown in the figures are model-based estimates derived from the fitted Cox model for each condition, where we condition on different age and PpgAge gap values. Average values for other covariates (except PpgAge gap) are used within age strata (defined as ± 5 years) for each chronological age plotted (35, 45, 55, 65, and 75, depending on the plot).
In supplemental Fig. S5, we conduct a sensitivity analysis where we refit models for each of the conditions within two age-specific subgroups. The threshold for defining these old vs. younger subjects are defined by the median age of events for that condition, so that the number of events within each subgroup are roughly the same. As before, we adjust for the same set of risk factors for each condition. In Fig. S6 of the supplement, we also show Kaplan–Meier curves, with 95% confidence intervals and number at risk over time, stratified by 3 PpgAge gap groups.
Further details about the data and analysis, including counts and followup time distributions, are in Section S4.
PPG-based age estimates and sleep behavior
Apple Watch employs an accelerometer-based algorithm to detect sleep stages throughout the night, categorized as “Awake”, “Deep”, “Core” and “REM”, available in the Health app45. Here, we study the association between Apple Watch sleep stages and PpgAge gap. For each night of successfully logged sleep, we extract the following sleep-related variables: (i) total sleep duration: total time spent in non-"Awake” stages, (ii) deep sleep duration: total time spent in the “Deep” stage, (iii) sleep efficiency: total sleep duration divided by the elapsed time from the onset of first non-"Awake” stage to the end of the final non-"Awake” stage, and (iv) REM latency: time from the onset of first non-"Awake” stage to the onset of first “REM” stage.
For each participant night, we compute age gap from segments collected between 10AM and 6PM (local time) of the following day. This yields a dataset at the participant-day level, where sleep-related variables and the biological age gap are paired. We then create a participant-level variation of this dataset by averaging the sleep-related variables and age gap for each participant. We then fit OLS models for age-matched groups as well as the entire population, where the target variable is the age gap and the explanatory variables are demographics, including chronological age, biological sex (mapped to 0 and 1), BMI, and the mentioned sleep-related variables. We calculated the variance inflation factor (VIF) between the explanatory variables, and observed no sign of multicollinearity between them with VIF = 1.11.
PpgAge and cardiovascular events
To investigate whether our PpgAge exhibits changes around the same time as other major physiological changes, we create a subset of participants who self-report having a cardiac event. We look into a number of different cardiac event types: a new diagnosis of coronary artery disease, peripheral artery disease, heart failure, or valvular disease; or a stroke, heart attack, CABG surgery, valve replacement surgery, or a cardiac stent and/or angiography. We also use a composite heart disease category that combines all of these event types together. As a reference comparison, we use a subset of the non-event “control” subjects and choose a random date in the middle of their study duration as the index date for day 0. We subset to the 180 days before and 180 days after the date of each event, and bucket events by month to avoid duplicated events. We only include events with at least 25 days of PpgAge estimates in each of the four non-overlapping 90-day periods around each event. After lowess-smoothing (locally weighted scatterplot smoothing) the PpgAge time series for each event and re-centering each time series to start 180 days before the event, we report the median and interquartile range for each event type. We also report the distribution of cumulative change in PpgAge within each of the 4 90-day windows before and after the event for a subset of event types, as well as a few representative individual-level time series of PpgAge around the time of event.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The Apple Heart and Movement Study data cannot be made publicly available due to privacy assurances included in the informed consent signed by the study participants, as well as contractual agreements between the entities conducting the study. Requests to access the data must be forwarded to the corresponding author, Dr. Andrew C. Miller. Requests should include name and contact details of the person requesting the data, which data and clinical variables are requested, and the purpose of requesting the data. Requests will be subject to review by the study teams at BWH and Apple under the guidance of the study PI, Dr. Calum MacRae, and will be evaluated under the terms of the informed consent and relevant contractual agreements. Time frame for a response will be approximately 3 months. As real data cannot be made publicly available, synthetic data are generated by accompanying code for the purpose of reproducing the study. Aggregated figure source data are provided. Source data are provided with this paper.
Code availability
Code for all data analyses and statistical modeling was written in Python 3.9 and R 4.3.3. We use pyspark for large-scale data queries, pytorch for SSL pre-training, scikit-learn and numpy for training age prediction models and computing confidence intervals (i.e., via the bootstrap), lifelines for survival analysis modeling, and matplotlib, seaborn (in Python), and ggplot2 (in R) for visualization. Code to reproduce the representation learning and analysis on synthetically generated data is available at https://github.com/apple/ml-ppg-age-analysis. The untrained model and training scripts can be found in the accompanying repository (within the training module). The architecture, initialization, and training in the accompanying repository match those used to train the model studied in this work, and can be used with user-provided data.
References
Vos, T. et al. Years lived with disability (ylds) for 1160 sequelae of 289 diseases and injuries 1990–2010: a systematic analysis for the global burden of disease study 2010. Lancet 380, 2163–2196 (2012).
Niccoli, T. & Partridge, L. Ageing as a risk factor for disease. Curr. Biol. 22, R741–R752 (2012).
U.S. Preventative Services Task Force. A & B Recommendations. link (Last accessed 06 April 2024, 2024).
Hamel, M. B. et al. Patient age and decisions to withhold life-sustaining treatments from seriously ill, hospitalized adults. Ann. Intern. Med. 130, 116–125 (1999).
Hadley, J. & Waidmann, T. Health insurance and health at age 65: implications for medical care spending on new medicare beneficiaries. Health Serv. Res. 41, 429–451 (2006).
United States Social Security Administration. Benefits. link (Last accessed 31 May 2024, 2024).
Ahadi, S. et al. Personal aging markers and ageotypes revealed by deep longitudinal profiling. Nat. Med. 26, 83–90 (2020).
Elliott, M. L. et al. Disparities in the pace of biological aging among midlife adults of the same chronological age have implications for future frailty risk and policy. Nat. Aging 1, 295–308 (2021).
Sherertz, E. F. & Hess, S. P. Stated age. N. Engl. J. Med. 329, 281–282 (1993).
Hwang, S. W., Atia, M., Nisenbaum, R., Pare, D. E. & Joordens, S. Is looking older than one’s actual age a sign of poor health? J. Gen. Intern. Med. 26, 136–141 (2011).
Wei, J. Y. Age and the cardiovascular system. N. Engl. J. Med. 327, 1735–1739 (1992).
Cohen, A. A. et al. Lack of consensus on an aging biology paradigm? A global survey reveals an agreement to disagree, and the need for an interdisciplinary framework. Mech. Ageing Dev. 191, 111316 (2020).
Moqri, M. et al. Biomarkers of aging for the identification and evaluation of longevity interventions. Cell 186, 3758–3775 (2023).
Kennedy, B. K. et al. Geroscience: linking aging to chronic disease. Cell 159, 709–713 (2014).
Kaeberlein, M., Rabinovitch, P. S. & Martin, G. M. Healthy aging: the ultimate preventative medicine. Science 350, 1191–1193 (2015).
Sierra, F. & Kohanski, R. Geroscience and the trans-NIH Geroscience Interest Group, GSIG. GeroScience 39, 1–5 (2017).
Lee, M. B. & Kaeberlein, M. Translational geroscience: from invertebrate models to companion animal and human interventions. Transl. Med. Aging 2, 15–29 (2018).
Horvath, S. DNA methylation age of human tissues and cell types. Genome Biol. 14, 1–20 (2013).
Hannum, G. et al. Genome-wide methylation profiles reveal quantitative views of human aging rates. Mol. Cell 49, 359–367 (2013).
Belsky, D. W. et al. Dunedinpace, a DNA methylation biomarker of the pace of aging. eLife 11, e73420 (2022).
Waziry, R. et al. Effect of long-term caloric restriction on DNA methylation measures of biological aging in healthy adults from the calerie trial. Nat. Aging 3, 248–257 (2023).
Attia, Z. I. et al. Age and sex estimation using artificial intelligence from standard 12-lead ECGs. Circ.: Arrhythm. Electrophysiol. 12, e007284 (2019).
Lima, E. M. et al. Deep neural network-estimated electrocardiographic age as a mortality predictor. Nat. Commun. 12, 5117 (2021).
Brink-Kjaer, A. et al. Age estimation from sleep studies using deep learning predicts life expectancy. npj Digit. Med. 5, 103 (2022).
Sun, H. et al. Brain age from the electroencephalogram of sleep. Neurobiol. Aging 74, 112–120 (2019).
Cole, J. H. & Franke, K. Predicting age using neuroimaging: innovative brain ageing biomarkers. Trends Neurosci. 40, 681–690 (2017).
Ahadi, S. et al. Longitudinal fundus imaging and its genome-wide association analysis provide evidence for a human retinal aging clock. eLife 12, e82364 (2023).
Tian, Y. E. et al. Heterogeneous aging across multiple organ systems and prediction of chronic disease and mortality. Nat. Med. 29, 1221–1231 (2023).
Charlton, P. H. et al. Wearable photoplethysmography for cardiovascular monitoring. Proc. IEEE 110, 355–381 (2022).
Pyrkov, T. V., Sokolov, I. S. & Fedichev, P. O. Deep longitudinal phenotyping of wearable sensor data reveals independent markers of longevity, stress, and resilience. Aging (Albany NY) 13, 7900 (2021).
Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 28, R1 (2007).
Aoyagi, T. Pulse oximetry: its invention, theory, and future. J. Anesth. 17, 259–266 (2003).
RCoP, L. National Early Warning Score (News): Standardising the Assessment of Acute-Illness Severity in the NHS. Report of Working Party. (Royal College of Physicians, London, 2012).
Charlton, P. H. et al. Assessing hemodynamics from the photoplethysmogram to gain insights into vascular age: a review from vascagenet. Am. J. Physiol.-Heart Circ. Physiol. 322, H493–H522 (2022).
Takazawa, K. et al. Assessment of vasoactive agents and vascular aging by the second derivative of photoplethysmogram waveform. Hypertension 32, 365–370 (1998).
Hernando, D., Roca, S., Sancho, J., Alesanco, Á. & Bailón, R. Validation of the Apple Watch for heart rate variability measurements during relax and mental stress in healthy subjects. Sensors 18, 2619 (2018).
Perez, M. V. et al. Large-scale assessment of a smartwatch to identify atrial fibrillation. N. Engl. J. Med. 381, 1909–1917 (2019).
Apple. Using Apple Watch to measure heart rate, calorimetry, and activity. link (Last accessed 20 November 2024, 2024).
Castaneda, D., Esparza, A., Ghamari, M., Soltanpur, C. & Nazeran, H. A review on wearable photoplethysmography sensors and their potential future applications in health care. Int. J. Biosens. Bioelectron. 4, 195 (2018).
Elgendi, M. On the analysis of fingertip photoplethysmogram signals. Curr. Cardiol. Rev. 8, 14–25 (2012).
MacRae, C. A. Apple heart & movement study. Clinical trial registration NCT04198194, clinicaltrials.gov. https://clinicaltrials.gov/study/NCT04198194. Submitted: November 13, 2019 (2021)
Abbaspourazad, S. et al. Large-scale training of foundation models for wearable biosignals. In The Twelfth International Conference on Learning Representations (eds Chaudhuri, S. et al.) (2024).
Pillai, A., Spathis, D., Kawsar, F. & Malekzadeh, M. PaPaGei: Open Foundation Models for Optical Physiological Signals. In The Thirteenth International Conference on Learning Representations (2025).
Apple. appleExerciseTime: the amount of time that the user has spent exercising during the specified day. link (Last accessed 17 October 2024, 2024).
Apple. Estimating sleep stages from Apple Watch. link (2023).
Shaffer, F. & Ginsberg, J. P. An overview of heart rate variability metrics and norms. Front. Public Health 5, 290215 (2017).
Pham, H. et al. The effects of pregnancy, its progression, and its cessation on human (maternal) biological aging. Cell Metab. 36, 877–878 (2024).
Poganik, J. R. et al. Biological age is increased by stress and restored upon recovery. Cell Metab. 35, 807–820 (2023).
Rutledge, J., Oh, H. & Wyss-Coray, T. Measuring biological age using omics data. Nat. Rev. Genet. 23, 715–727 (2022).
González, Ld. M., Romero-Orjuela, S. P., Rabeya, F. J., Del Castillo, V. & Echeverri, D. Age and vascular aging: an unexplored frontier. Front. Cardiovasc. Med. 10, 1278795 (2023).
Athey, S., Chetty, R. & Imbens, G. The Experimental Selection Correction Estimator: Using Experiments to Remove Biases in Observational Estimates. No. w33817. (National Bureau of Economic Research, 2025).
Karlsson, B., Knutsson, A. & Lindahl, B. Is there an association between shift work and having a metabolic syndrome? Results from a population based study of 27 485 people. Occup. Environ. Med. 58, 747–752 (2001).
Wang, F. et al. Meta-analysis on night shift work and risk of metabolic syndrome. Obes. Rev. 15, 709–720 (2014).
Belsky, D. W. et al. Quantification of biological aging in young adults. Proc. Natl. Acad. Sci. USA 112, E4104–E4110 (2015).
Devlin, J., Chang, M.-W., Lee, K. & Toutanova, K. Bert: pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, volume 1 (long and short papers), 4171–4186 (2019).
OpenAI. GPT-4 technical report. Preprint at https://arxiv.org/abs/2303.08774 (2023).
Chen, T., Kornblith, S., Norouzi, M. & Hinton, G. A simple framework for contrastive learning of visual representations. In International Conference on Machine Learning, (eds Daumé, III, H.& Singh, A.) 1597–1607 (PmLR, 2020).
Chen, X., Xie, S. & He, K. An empirical study of training self-supervised vision transformers. In Proceedings of the IEEE/CVF international conference on computer vision, 9640–9649 (2021).
Oquab, M. et al. DINOv2: Learning Robust Visual Features without Supervision. Trans. Mach. Learn. Res. https://openreview.net/forum?id=a68SUt6zFt (2024).
Baevski, A., Zhou, Y., Mohamed, A. & Auli, M. wav2vec 2.0: a framework for self-supervised learning of speech representations. Adv. Neural Inf. Process. Syst. 33, 12449–12460 (2020).
Baevski, A. et al. data2vec: a general framework for self-supervised learning in speech, vision and language https://arxiv.org/abs/2202.03555 (2022).
Smith, S. M., Vidaurre, D., Alfaro-Almagro, F., Nichols, T. E. & Miller, K. L. Estimation of brain age delta from brain imaging. Neuroimage 200, 528–539 (2019).
CDC. About adult BMI. link (Last accessed 28 May 2024, 2022).
Acknowledgements
The authors wish to thank all participants in the Apple Heart & Movement Study, without whom this research would not be possible, as well as partners at the American Heart Association and Brigham and Women’s Hospital. The authors also thank the following individuals for thoughtful discussion and guidance in support of this work: Calum MacRae, Antoine Wehenkel, Fahad Kamran, Rajiv Kumar, Jen Block, Adam Phillips, James Truslow, Joe Schmitt, Matt Bianchi, and Chris Curry. And for additional support, the authors thanks Mira Chiang, Jonathan Varbel, and Peter Gray.
Ethics declarations
Competing interests
The following authors are employed by Apple, Inc. and own Apple, Inc. stock: A.C.M., J.F., C.H.D., S.A., S.E., I.S., and G.S. The Apple Heart & Movement Study receives funding from Apple, Inc. and the American Heart Association.
Peer review
Peer review information
Nature Communications thanks Francesco Prattichizzo, Peter Charlton and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Miller, A.C., Futoma, J., Abbaspourazad, S. et al. A wearable-based aging clock associates with disease and behavior. Nat Commun 16, 9264 (2025). https://doi.org/10.1038/s41467-025-64275-4
Received: 20 June 2024
Accepted: 12 September 2025
Published: 20 October 2025
DOI: https://doi.org/10.1038/s41467-025-64275-4
.png)