Activity annealing leads to a ductile-to-brittle transition in amorphous solids

In biological matter, where dense packings and self-propulsion coexist, the physics of glasses^1,2,3,4,5,6 and active systems^7,8,9,10 come together in new ways. Many aspects of glassy physics have now been seen at both the intercellular and the intracellular levels^{11,12,13,14,15,16}. The fact that these materials in vivo are packed in a variety of conformations and geometries, such as two-dimensional epithelial layers on organ surfaces or tightly tangled proteins within cell cytoplasm, adds an additional layer of complexity to understanding their dynamics. Understanding these dynamics and how cells regulate the glassiness has important consequences. It is known that many diseased cells lose the ability to vitrify or show different fragility behaviour than their healthy counterparts¹⁷. ‘Correct’ cell shapes and tissue rigidity can serve as markers for health, and any anomaly can be potentially used as a diagnostic tool.

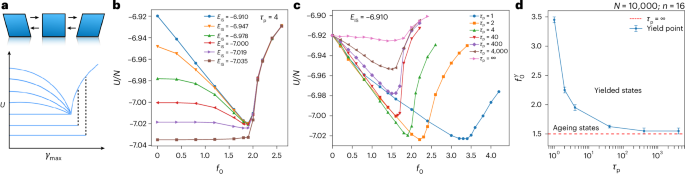
In this Article, we investigate how self-propulsion regulates glassiness in active glasses. In particular, we focus on the fluidization transition that enables the system to transition from a jammed state to a flowing state. We find that the yielding of glasses under internal active forcing parallels the yielding of structural glasses seen under oscillatory shear. The active yielding diagram in Fig. 1b displays all the characteristics typically observed under cyclic shear yielding, shown as a schematic in Fig. 1a. We observe an annealing regime where activity anneals the glasses, noting that this activity-induced annealing is highly sensitive to the initial state. Poorly annealed glasses experience the most significant effect, whereas well-annealed glasses show almost no effect. Beyond a critical threshold, the curves collapse to a single value and the annealing history of the sample is lost. This represents the ergodic, fluidized state.

Fig. 1: Annealing and yielding in glasses via local perturbations due to activity.

a, Schematic of the yielding process in glasses under oscillatory shear, with oscillation strain amplitude γ_max being the control parameter. Poorly annealed glasses (having larger potential energy, U) anneal much better with increasing γ_max compared to well-annealed glasses, which show little to no annealing. Beyond the yielding amplitude \({\gamma }_{{\mathrm{max}}}^{Y}\), the system forgets its annealing history entirely. b, Effects of active dynamics with τ_p = 4 (carried out for a time window of t_w) on glasses having various inherent state energies. Up to a threshold of f₀ = 1.9 for this model, we see enhanced ageing behaviour, as seen by the system’s progression towards deeper and deeper minima. Beyond this threshold, the various curves collapse to a single curve, denoting a yielded state where the system no longer retains a memory of its initial preparation. Similar to cyclic shearing, we also observe that poorly annealed glasses respond much better to annealing via active forcing compared to well-annealed glasses, which have little to no annealing. c, Variation of the yielding curve corresponding to E_IS = −6.910 (the enveloping curve in b) with persistence time. We observe the yield point shift to higher values of f₀ with decreasing τ_p. This behaviour is consistent if one qualitatively maps the active tumbling frequency 1/τ_p to the oscillation frequency in the cyclic shearing case. There, too, with increasing oscillation frequency, a shift in the yielding amplitude γ_yield to a higher value is observed. d, A state diagram depicting the ageing versus yielded states, separated by a yield line obtained by plotting the yielding force \({f}_{0}^{\;Y}\) versus τ_p from c. The error bars are bounded by the points of lowest energies and the first point where the energies begin to rise, and their means mark the yield points in d. System size of N = 10,000 particles, averaged over n = 16 ensembles.

Both the annealing and the fluidizing effects of the activity observed could have practical implications in nature. For instance, tardigrades are known to undergo intracellular vitrification when faced with harsh conditions as a self-preserving mechanism¹⁸. It is conceivable that natural selection could exploit low levels of activity (that is, below the fluidization threshold) for rapid vitrification when conditions change abruptly for the worse. Another consequence of the annealing aspect of the phase diagram is that systems with activity will tend to go to better packings as time progresses, thus resulting in more closely packed tissues. The internal activity could similarly influence the ageing and maturation of tissues, resulting in effects like a gradual increase in tissue rigidity with age. The fluidization regime has its role in morphogenesis, wound healing, cancer metastasis and so on and has also been observed in model active glasses before¹⁹.

Earlier studies comparing yielding under simple sheared glasses and dense active matter have reported different critical behaviour between the two systems²⁰, which contrasts with the findings previously proposed²¹. Additionally, the contrasting previous study²¹ introduced a cyclic reversal protocol in an infinitely persistent, velocity-controlled active system and reported similarities, including reversible-irreversible transition generally seen in cyclically sheared systems. Here, first, we make the correspondence to oscillatory shear concrete by discussing critical phenomena-like behaviour of diverging time scales and nature of memory formation and show similarities in the microscopic picture of annealing by demonstrating the importance of stress reversals in both cases. We also discuss the ways in which the dynamics differ, activity being stress/force controlled, whereas shearing usually is strain/deformation controlled, and how these can account for the subtle differences observed. Next, we examine the mechanical response of such states. A wide variety of parameters are known to influence the failure mode in glasses. For instance, altering the confining geometry^22,23,24, adjusting the range of interparticle interactions²⁵, introducing inclusions into the embedding matrix²⁶ and varying preparation or annealing history²⁷ can all control the type of failure that occurs. In our study, we focus on annealing (induced by activity), sample geometry and the two active forcing parameters. Because biological tissues experience a range of stresses throughout their lifetimes and show a plethora of failure modes (bones snap, epithelia ruptures, muscles ‘strain’, and so on), a complete understanding of yielding in active glasses under external loading might help us understand some of these phenomena. We first show that activity can anneal a poorly annealed (ductile) glass so much as to make it brittle. If the sample geometry can accommodate it, failure occurs via shear band formation. In the presence of activity, we observe that the heterogeneous yielding via shear band formation can be tuned to more homogeneous yielding at high enough forcing magnitudes f₀, but it can be tuned back to a heterogeneous one, again by increasing persistence time τ_p. Thus, appropriate tuning of the active forcing parameters will lead to either enhancement or suppression of shear band formation.

The fact that activity can anneal glasses effectively merits being stated separately from the context of yielding. It could also be thought of as a stand-alone method for annealing, alongside techniques like physical vapour deposition²⁸, swap Monte Carlo²⁹, in silico vapour deposition³⁰ and, of course, annealing via oscillatory shearing^31,32,33. We previously alluded to these annealing effects of activity in our work dealing with the formation of cavities in glasses³⁴.

For our simulations, we use a three-dimensional binary Kob–Anderson (KA) mixture³⁵, with an additional ‘run and tumble’ forcing applied to the smaller ‘B-type’ particles. Both the persistence time, τ_p (in reduced units), and the magnitude of active forcing, f₀, are taken to be the control parameters. System sizes varied, ranging from N = 10,000 for annealing studies to N = 32,000 to 128,000 for tensile testing. States were sampled during the annealing process for energy minimization using the conjugate gradient method. A detailed overview of the system, simulation details and all protocols used can be found in the Methods.

Annealing and yielding diagram

Figure 1b encapsulates the outcome of our annealing protocol. We report a trend that is remarkably similar to the one observed in ref. ³⁶, where the annealing is performed using oscillatory shearing and under athermal conditions. A schematic for the same is depicted in Fig. 1a for easy comparison. Active glasses appear to age faster, enabling them to reach lower points in their potential energy landscape than their inactive counterparts. Up to a certain threshold f₀, we observe annealing beyond which the energies again begin to rise and collapse to a single curve. For the time evolution of inherent state energies under active dynamics, see Supplementary Fig. 1. In reference to our study, there have been recent reports in ref. ³⁷ of analogous outcomes observed in two dimensions for the KA binary mixture of particles. Drawing an analogy with the yielding amplitude of oscillation (\({\gamma }_{\rm{max}}^{Y}\)) seen in oscillatory shear simulations, we term this the active yielding amplitude (\({f}_{0}^{\it{Y}}\)). In our case, we find \({f}_{0}^{\it{Y}}\simeq 1.95\). The various curves collapsing to a single curve beyond \({f}_{0}^{\it{Y}}\) signifies that the system no longer remembers its original preparation history and thus can no longer be in the ageing regime.

We also observe that poorly annealed glasses respond much better to annealing via activity than well-annealed glasses. This trend, too, resonates with that reported in oscillatory shearing. One way to understand this is to realize that poorly annealed glasses have more ‘soft spots’ or shear transformation zones^38,39,40 that are available to be triggered by the microscopic perturbations caused by active forcing. A dearth of such soft spots in well-annealed glasses also explains their low sensitivity to both active and oscillatory annealing.

In Fig. 1c, we observe how the enveloping curve in Fig. 1b changes with change in τ_p. First, we observe that the yielding magnitude shifts to higher values of f₀ as the persistence time is decreased (or the tumbling frequency is increased). This is also what one observes in the oscillatory shear case, if one increases the oscillation frequency. Thus Fig. 1b,c together hint at a mapping between the two active parameters (f₀ and τ_p) and the two shearing parameters (γ_max and ω). Tracking the yield point, we draw a state diagram in Fig. 1d separating the ageing and the yielding states. Another thing to note in Fig. 1c is the non-monotonic dependence of annealing efficiency with τ_p for a given f₀. We expand on this in detail in the coming sections.

One crucial difference to note is that athermal cyclically sheared glasses always reach a limit cycle below the yielding amplitude. The active system, however, continues to remain in a logarithmically decaying ageing regime. This can be explained by realizing that the two systems differ in one crucial way: athermal cyclic shear is usually strain/deformation controlled, whereas the active system is stress/force controlled. In athermal strain-controlled systems, below yielding, the glass is constrained to explore only a finite subset of the landscape dictated by the applied deformation. In force-controlled systems, however, ‘creep-like’ phenomena can always happen, taking the system out of any absorbing state. To demonstrate this conclusively, we have also conducted stress-controlled oscillatory shear experiments while keeping the oscillation frequency fixed (akin to keeping τ_p fixed). Here, as well, we saw continued ageing below the yield point, and the system did not reach a steady state, with the qualitative nature of the yielding curve being similar to the active case. The results for the stress-controlled oscillatory shear can be found in Supplementary Fig. 2. Videos for the same are also attached. Finite, albeit low, bath temperatures, as well as the random nature of active forcing, might also be partly responsible.

Because our system lacks any steady states below yielding, we take a large finite time window instead (~10⁵ time units) to get a sense of the limiting energies. The exact values in Fig. 1b,c will depend on this waiting period (t_w); however, the qualitative nature of the yield curve remains the same. Such waiting-time dependence is a hallmark of ageing systems, and active glasses have been shown to display complex ageing behaviours^41,42. The detailed analogy presented here should help strengthen the links seen earlier between active and sheared granular systems^21,43.

Diverging time scales to steady states

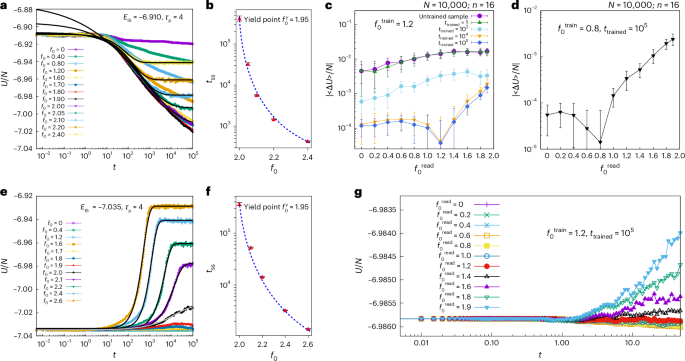
Diverging time scales to a steady state from both above and below yielding is a characteristic of glasses yielding under athermal cyclic shear. In Fig. 2b,f, we report diverging time scales to a steady state when approached from above yielding for the active case as well. The times to steady state t_ss in panels Fig. 2b,f are calculated by fitting the energy evolution curves for poorly annealed case (Fig. 2a) and the well-annealed case (Fig. 2e), respectively, to stretched exponential fits. Under oscillatory shear, the time scale to steady state is known to diverge as a power law, \({t}_{\rm{ss}} \approx | {\gamma }_{\rm{max}}-{\gamma }_{\rm{max}}^{\it{Y}}{| }^{-\eta }\), with the exponent η ≈ 2.8 (ref. ³⁴). The exponent is known to vary with changing fragility⁴⁴. The time scales for the active case also show a similar power-law-like divergence as \({t}_{\rm{ss}} \approx |\;{f}_{0}-{f}_{0}^{\;\it{Y}}{| }^{-\eta }\), with exponent η ≃ 3.7 for the poorly annealed case and η ≃ 2.5 for the well-annealed one. These fits can be found in Supplementary Fig. 3. Below yielding, as already stated, our system does not show any steady states primarily because the active system is force controlled and not deformation controlled²¹. However, here we should also point out that there exists an oscillatory shear protocol, where even under strain control, the system resists reaching an absorbing state below yielding. For instance, in random multidirectional oscillatory shear, if the direction of oscillation is randomized to an orthogonal direction after each cycle, the system cannot find an absorbing state, and the existence of such a steady state remains an open question³³. Because after persistence time, the forces in the active case are randomized and not just reversed; one could think that the active case maps better to random multidirectional oscillatory shear. Absorbing states have, in fact, been reported under protocols where active directions are instead reversed (rather than randomized) and where activity is velocity controlled (rather than force controlled)²¹. This further strengthens the rationale provided for the absence of the same in our system. Continued logarithmic ageing is also seen in the presence of oscillatory shearing under finite temperatures³², and because our system is at a finite albeit low temperature, this too could, in part, explain the absence of steady states below yielding.

Fig. 2: Time evolution of energy and memory effects.

a,b,e,f, Evolution of inherent state energies and diverging time scales to reach the steady state as one approaches the yielding amplitude from above, shown for poorly annealed (a,b) and well-annealed (e,f) glasses. The time to steady state (t_ss) is calculated by fitting it to a stretched exponential (shown by plain lines in a and e). The error bars in b and f are estimated based on the errors in the fitting parameters of the stretched exponential fits (using least squares fitting), and the blue dashed lines serve as a guide for the eyes. c,d, States sampled from the annealing trajectory of poorly annealed glasses at various times are shown to retain a memory of the magnitude of the annealing force f₀. This memory shows up in the transient annealing signature during ‘parallel reading’, in which copies of the encoded samples are subjected to various reading amplitudes. The sharp kinks, which develop with increasing time under training, observed at the reading amplitudes of 1.2 (c) and 0.8 (d), constitute memory readouts. Data are mean ± s.d. g, Time evolution of the inherent state energy during one such parallel reading process. The encoded amplitude shows the least absolute change in energy during the small reading window. The persistence time is taken to be the same (τ_p = 4) for both reading and writing. System size N = 10,000, averaged over n = 16 independent ensembles.

Memory encoding and reading

Glasses subjected to repeated deformation cycles encode in themselves the memory of the driving amplitude γ_max (refs. ^45,46). This amplitude can then be read off using various protocols, parallel and sequential reading being two of the most popular ones. Here, encoding involves multiple repeated cycles at the training amplitude, and reading (parallel) involves the application of a single cycle with increasing amplitudes. The mean squared displacement with respect to the trained state after each cycle is then plotted, and memory manifests itself as a kink in this curve. For the active case, we show that the annealing process is also a memory-encoding process. Thus, encoding involves annealing a poorly annealed sample using activity for a long time. We then sample these (non-energy-minimized) trained states. Reading involved restarting the dynamics by giving fresh velocities to the particles and applying increasingly large f₀ to copies of the trained samples for a short time (a few ‘active cycles’) and measuring the change in some dynamical quantity with respect to the trained reference. Here, we look at the annealing response itself, or the average change in energy per particle 〈ΔE〉/N. A clear memory signature can be seen in Fig. 2c,d. The absence of a prominent transient annealing response at the encoding amplitude thus encodes the memory. Reading memory from the absence of a transient has been seen in suspensions in Couette cells, pulse sign memory, assembly of gears and so on, or the Bauschinger effect in amorphous materials⁴⁷. But what is the nature of such a memory? Is it return point memory or just the memory of the last driving? Both are seen in sheared glasses. To answer this, we show that this memory develops gradually over time (Fig. 2c), just as it does with an increasing number of cycles under oscillatory shearing. In Fig. 2g, we see the evolution of the inherent state energy during parallel reading. Although the transient increase in energy for reading amplitude higher than the training amplitude is somewhat expected, the decrease in energy for smaller values of \(f_{0}\), as observed, needs an explanation. In fact, it gives us valuable insights into how activity traverses the glass landscape. The presence of a transient response for values of \(f_{0}\) both below and above the training f₀ indicates that active dynamics with a particular f₀ at a particular τ_p leads the glass to a very specific region in the energy landscape, which can be attained by that combination alone. Any change in the ‘search algorithm’, for instance, by lowering f₀, allows the glass to explore regions with lower energies that it might have ‘jumped over’ with its higher training step determined by \({f}_{0}^{\rm{train}}\) and τ_p. In fact, this exact phenomenon is seen in the case of cyclic shearing as well. If one takes a trained state (one that has reached an absorbing state) and applies additional cycles with amplitudes smaller than γ_trained, one sees that annealing begins again, and the system now reaches a new absorbing state within a few cycles⁴⁶. Such a retrained sample then shows multiple persistent memories in the oscillatory athermal quasistatic shear (AQS) case. Whether the active system allows for multiple persistent memory storage is an interesting area to explore and requires further studies. However, the similar response to retraining at a smaller amplitude suggests that both activity and cyclic shear traverse the glassy landscape in a very similar manner.

Note that apart from the mechanical response, ‘rigidity’ caused by annealing via activity could manifest itself in a very different manner in places like neuronal tissues. Recent studies have reported the effects of activity in enhancing associative memory in prototypical memory formation models like the Hopfield model⁴⁸. Here, we show that repeated active forcing, apart from annealing the tissue and making it more rigid, also encodes a memory in the structural glass. By demonstrating that memory encoding and retrieval is possible using only local active driving, our work could have implications in understanding memory storage and retrieval in biological systems where local metabolic activity is the sole regulating parameter present. On a more speculative note, annealing caused by neuronal activity, for instance, might have a role in brains becoming less plastic (losing the ability to learn new things) with age.

Mechanism of annealing and importance of stress reversals

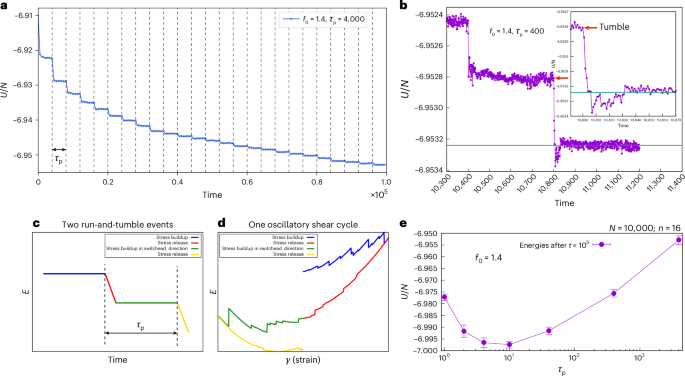
To understand the mechanism behind the annealing effects of activity having a finite persistence time, we take a look at the energy profile for activity with a relatively large persistence time (Fig. 3a). One sees that the energy goes down ‘stroboscopically’ after every τ_p time. In Fig. 3b, we also observe that most of the annealing takes place right after the forces switch directions or right after the tumbling event and then quickly saturates to a relatively stationary value during the remaining ‘run’ (barring a few rare events). After the tumble, the glass gets new directions to explore in the landscape, thus resulting in a quick decrease in energy. One also notes that during most of the trajectory, the glass is not annealing; it anneals only moments after the tumble. Thus, from an exploration versus exploitation point of view, such a large value of τ_p is not optimal as ‘running time’ is far too large. If one switches more frequently, one might get more annealing during the same period. However, if one switches too frequently, one will not exploit the new search directions optimally. Thus, one expects to see a non-monotonic dependence of annealing efficiency with τ_p for the same value of f₀. This is indeed what we see in Fig. 3e. A cross-section at f₀ = 1.4 in Fig. 1c shows that annealing becomes more and more efficient until around τ_p = 4, and then the saturation energy begins to rise again with a further decrease in τ_p. By looking in at one of these run-and-tumble cycles in higher resolution (Fig. 3b), one could get an estimate for the optimal τ_p value. Thus, we now have a mechanistic understanding of how annealing proceeds in active glasses; in particular, we have an idea of the time scale over which the annealing happens after a tumble. Thus allowing one to optimize for maximal annealing for a particular driving force. How temperature interferes with this annealing seems to be an interesting and non-trivial area to explore if one aims to come up with protocols that maximize annealing efficiency. At very low temperatures, such as the one used here, we are in the regime of activity-driven search in the landscape. Whether adding noise in the form of temperature enhances or decreases efficiency is an interesting question to address in the future. Incidentally, note that in cyclic shear, too, the annealing happens during the stress-release phase. In Fig. 3c,d, we identify an active cycle (consisting of two run-and-tumble events) and show qualitatively how it maps to the oscillatory shear cycle.

Fig. 3: Importance of stress reversals.

a, Ensemble-averaged annealing trajectory for poorly annealed glasses, evolving under a very large persistence time of τ_p = 4,000 and a forcing magnitude f₀ = 1.4. Vertical dashed lines are marked at intervals of persistence time. We note that the majority of the annealing happens within a short time after the forces randomize their directions (the tumbling event). b,e, Two such tumbling events in high resolution for f₀ = 1.4 and τ_p = 400 (b). Inset in b shows the system finishes exploring the majority of the minimas within ~10 time units after the tumble (pointed by the red arrow). This can be used to estimate the optimal value of τ_p for annealing given the f₀. Any τ_p larger than ~10 would waste time exploring directions already exhausted, and any τ_p less than this would hinder the annealing process by not exploiting that direction for long enough. This results in a non-monotonic dependence of annealing efficiency on τ_p (e). Drawing parallels from the cyclic shear case, a natural definition of a ‘cycle’ in the active case emerges as well. Data in e are mean ± s.d. c,d, An ‘active cycle’ (c) and a qualitative mapping to an oscillatory shear cycle (d). In both systems, annealing follows stress reversals, underscoring the importance of a finite persistence time for active systems.

Biological tissues come in a variety of forms, from soft tissues such as muscles to hard ones like bones. Then there are tissues like cartilage, which are intermediate in terms of rigidity. Depending on their location and function in the body, they withstand a variety of stresses throughout their lifetime. The failure mechanisms of these tissues are different, too. One can sprain a muscle by overstretching it, or one can fracture a bone by snapping it. A recent study also reported motility-induced abrupt fractures in animal epithelia⁴⁹. Because biological tissues are under constant stress and experience a variety of loadings (both external and internal) throughout their lifetime, it becomes relevant to study how internal activity affects their failure modes.

Although looking at the decrease in the inherent state energies in amorphous solids gives us some hints (Fig. 1b,c), it does not necessarily convey how drastic the effect of annealing due to active particles could be on the mechanical properties of the system. In the following two sections, we first show that just via annealing through internal activity, the whole range of toughness seen in biological tissues can be accessed. Thus, regulating internal activity provides a means by which tissues can control their ductility. This might shed light on the origin of such brittle tissues and how activity during embryogenesis and development might have a role in forming such tissues in the first place. Moreover, we also study in detail the role played by strain rate in dictating the response in such systems. Because a true brittle response is facilitated by the formation of a shear band, we show that well-annealed active glasses with correct sample geometry can fracture via shear band formation as well, and we explain how the active parameters f₀ and τ_p affect the stability of the shear band.

Ductile-to-brittle transition and effect of strain rate

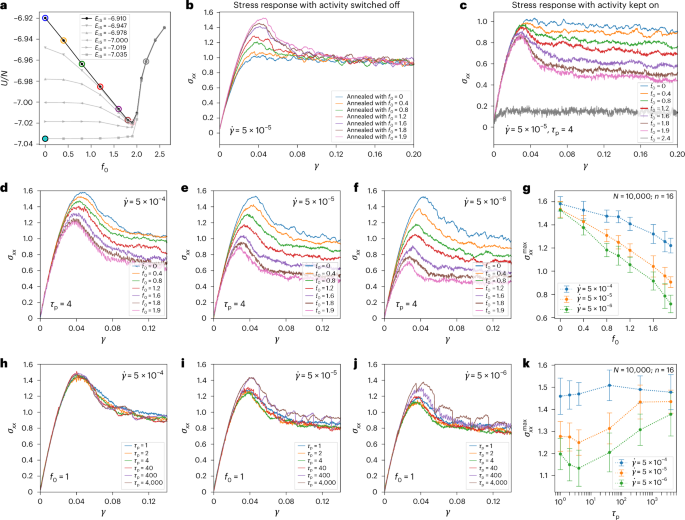
We conduct tensile testing of the active glass samples in open-boundary conditions, confined by walls along one side. The strain rate is controlled by pulling the walls in opposite directions. By first selecting the states marked by open circles along the least well-annealed (topmost) curve in Fig. 4a, we show that a brittle response develops in the states with an increasing degree of annealing. This response is preserved whether the annealing activity is turned off (Fig. 4b) or is kept on (Fig. 4c) during the tests. This is indicated by the development of a stress overshoot and drop (with respect to the steady-state stress), which develops with annealing. Note that in Fig. 4c, the saturation of the steady-state stress to different values is solely due to the states being pulled at different f₀ values. Given a particular f₀, the active states, too, would saturate to the same steady state independent of initial annealing (as demonstrated in Supplementary Fig. 4).

Fig. 4: Effect of strain rate on mechanical response of active amorphous solids.

a–c, States marked by open circles on the enveloping curve (a) are sampled for tensile testing (b,c). These states are colour-coded to match the corresponding stress-strain curves in b and c. In b, the activity is switched off before the tests, whereas in c, the tests are performed by keeping the annealing activity on. We see a brittle response emerge with an increasing degree of annealing via activity in both cases, indicated by the appearance of larger and larger stress overshoots and drops (with respect to the steady-state stress). In the subsequent panels, we take the most well-annealed states available to us, marked by a filled cyan circle in a, and look at their stress response at various strain rates. d–f, Effect of changing f₀ at a constant persistence time for fast (d), intermediate (e), and slow (f) strain rates. g, Maximum yield stress goes down with increasing f₀ for all the strain rates considered. We also observe early yielding in active glasses as compared to the passive case. h–j, Effects of changing τ_p at a fixed forcing magnitude for fast (h), intermediate (i), and slow (j) strain rates. k, Depending on the strain rate, we observe a non-monotonic behaviour in the overshoot observed during yielding. Note the similarity of this to the non-monotonic behaviour of annealing efficiency shown in Fig. 3e. This signifies that for slow strain rates, the same pathways to relaxation that cause annealing are also engaged during the yielding process under external tension. At larger persistence times (compared to the strain rate), the active forces become more and more quenched during the linear part, and the glass is forced to take a non-optimal path through the landscape in order to yield, resulting in the stress overshoot observed. These results are for a system size of N = 10,000 averaged over n = 16 ensembles each. Data in g and k are mean ± s.d.

To focus on other aspects of the stress response in active glasses, we first need to isolate from the annealing effects of activity on the initial samples. We do this by sampling the most well-annealed states available to us (marked by the filled cyan circle in Fig. 4a, having per-particle inherent structure energy E_IS = −7.035), as these are the states that are least affected by further annealing due to activity. In Fig. 4d–f, we see the effects of strain rate by changing f₀ and keeping τ_p constant. The maximum yield stresses for the same are plotted against f₀ in Fig. 4g. We observe that the peak stresses go down with f₀, suggesting an effective temperature-like description⁵⁰ might hold. In passive systems, the peak stress has been shown to decrease as T^2/3 across a wide variety of amorphous solids^51,52, including metallic glasses. Although our results in active glasses are in qualitative agreement with this, a better understanding of whether T^2/3 behaviour with T being replaced by an appropriate effective temperature T_eff that depends on f₀ and τ_p will be an interesting future direction to pursue. One also notes that active systems yield at lower strains, suggesting that activity provides new stress-relaxation pathways to yield that are not available to the passive glass under pure tension. This is also in complete contrast to the effect of random pinning on the yield strain as reported in ref. ²⁶. Thus, active particles can be considered as fluidizing or antipinning centres that make the materials less rigid mechanically during deformation. However, they help to achieve stable mechanical states via annealing when allowed to relax.

In Fig. 4h–j, we now keep the active forcing f₀ constant and vary the persistence time to understand how intrinsic activity time competes with the other natural time in the system introduced by \(\dot{\gamma }\). The peak stresses under tension along the pulling axis (x axis), \({\sigma }_{xx}^{\rm{max}}\) are then plotted against τ_p in Fig. 4k for various strain rates. We see a gradual appearance of stress overshoot developing for larger persistence time at slower strain rates, and a non-monotonic behaviour with τ_p is seen. This can be rationalized as follows: at faster strain rates, the active forces are basically quenched along the same directions during the linear part of the stress-strain curve. Thus, at such short time scales, the system cannot discern between the various τ_p values, and thus we see the curves basically overlapping on top of each other. As the strain rate is decreased, the systems with shorter persistence times can explore more directions for stress relaxation, whereas for the larger persistence times, the active forces are still quenched. For larger τ_p values, the system has to yield through a non-optimal direction in the energy landscape, resulting in a stress overshoot. Also note the similarity of the non-monotonic nature of the \({\sigma }_{xx}^{\rm{max}}\) curves to the non-monotonic nature of annealing efficiency with τ_p in Fig. 3e, indicating the same mechanisms at play.

Shear banding in active glasses

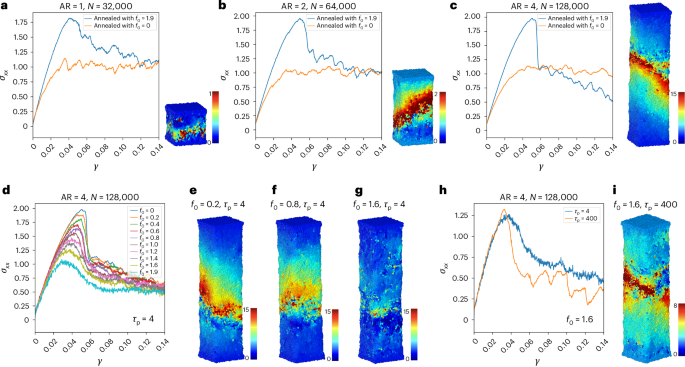
True brittle failures in glasses are mediated by shear band formation, and this requires larger system sizes and low inherent state energies²⁷. We first demonstrate that, in addition, system geometry is equally important to elicit a true brittle response mediated by shear band formation. For this, a cuboidal rod-shaped geometry having open boundaries confined by rigid walls along one dimension is considered. System sizes of N = 32,000, 64,000 and 128,000 are taken for the same. We study the effects of geometry by changing the aspect ratio (defined as \({\rm{AR}}=\frac{{L}_{x}}{{L}_{y}={L}_{z}}\), with x always being the long axis along which the tension is applied) while keeping the surface-to-volume ratio constant. We have considered aspect ratios of 1, 2 and 4, respectively, for the three system sizes taken. Here, in the original protocol, we introduce an additional time window of 5 × 10⁶ molecular dynamics (MD) steps. During this period, we anneal the system in an open geometry while it is still active—that is, after the periodic boundary conditions have been removed but before the loading has begun. We find that in the presence of these freshly formed surfaces, the system can be made to anneal even further with active forcing. This restarting of annealing that happens with activity demonstrates that activity can be a means to anneal open surfaces better. Figure 5a–c (along with the corresponding configurations, shown adjacent) shows the results of conducting the tension experiments on the post-annealed states thus formed: that is, under passive conditions. We observe that because under tension, shear bands in glasses form at 45° (ref. ²³), only AR > 1 can accommodate them. For AR = 1 in Fig. 5a, there is significant interference by the walls for a sharp shear band to form. This can be noted from the gradual yielding seen in the stress-strain curve for the same. In Fig. 5b, with AR = 2, we see the sharpness of the stress drop increase, with it becoming nearly discontinuous for the AR = 4 case in Fig. 5c. Thus, given the same annealing history, only aspect ratios larger than 1 would show clear shear band formation, even in the passive case. We further demonstrate that this is indeed a geometric effect dependent on the aspect ratio by discounting the effect of system size (Supplementary Fig. 5). The effect of annealing also reflects on the relative elongation before complete fracture, which can be seen in Supplementary Fig. 6.

Fig. 5: Effects of geometry and activity on shear band formation.

The colour bar denotes the magnitude of squared displacements. a–c, Given the same annealing history with activity, a sharp shear band develops (in the passive case, post-annealing) only if the aspect ratio is greater than 1, as seen for AR = 2 (b) and AR = 4 (c). Below this, the shear band formation at 45° is geometrically hindered by the fixed walls on both ends (a). d, Effect of f₀ on shear band formation in well-annealed glasses. For a given persistence time (here, τ_p = 4), a gradual loss of sharp shear band is noted when the tensile testing is done in the presence of activity with larger and larger f₀ values. e–g, Configurations depicting the shear band formed under f₀ = 0.2 (e), becoming progressively more diffused when the glass yields under larger values of f₀ (0.8 in f and 1.6 in g). h,i, The brittle shear band response lost with higher f₀ can be recovered by increasing the persistence time as seen from the stress-strain curve in h and in the corresponding sample configuration in i. Thus, while increasing f₀ suppresses shear band formation, larger persistence times promote it. To resolve the sharp stress drop associated with shear band formation, stress-strain curves for individual samples are depicted. A fixed \(\dot{\gamma }=5\times 1{0}^{-5}\) is taken throughout.

Now, taking the correct geometry that supports shear banding in passive glass, we can begin to understand the effects of active forcing on shear band formation. Figure 5d–g shows the results for yielding in active glasses under tension for AR = 4 and system size N = 128,000. In Fig. 5d, we take a glass annealed well by activity and change f₀ during the loading phase. τ_p is kept fixed throughout. We see that increasing f₀ can gradually destroy the shear band formation. This is apparent from the stress-strain curves shown in Fig. 5d, as well as the corresponding configurations for the same displayed in Fig. 5e–g. Thus, one can go from a heterogeneous shear band mediated yielding to more homogeneous yielding with increasing f₀ at smaller τ_p. This behaviour is very similar to an effective temperature-like description, as with increasing temperature, yielding becomes more homogeneous and shear band formation becomes rare. On the other hand, the effect of changing τ_p at a fixed f₀ seems to show a contrasting behaviour, as shown in Fig. 5h,i. We see that shear band formation can be recovered at larger persistence times. This is indicated by a clear overshoot and a much sharper stress drop near yielding strain observed in the high τ_p case. Additional results for high τ_p can be found in Supplementary Fig. 7. Thus, the physics of active yielding seems to be very rich, and further studies are needed to better understand this phenomenon.

Our study on yielding in active glasses reveals a strong correspondence with the annealing and yielding processes observed in glasses subjected to oscillatory shear. We discovered that the yielded part of the yielding diagram could account for how fluidization in tissues and other biological matter might set in due to internal activity. Concurrently, the annealing part potentially contributes to gradual stiffening in these tissues, implicating internal activity in age-related tissue stiffness. To solidify the correspondence, we first show diverging time scales to steady state as is observed for yielding under oscillatory shear. We then show that just like repeated cyclic shear encodes the memory of the oscillation amplitude γ_max, the active force magnitude f₀ too encodes itself in the states annealed by activity. We introduce a way to read this by looking at the transient annealing response of the encoded states. Furthermore, we show that the microscopic picture of annealing in both cases is similar enough to allow for a qualitative mapping of a shear cycle to two ‘run-and-tumble events’ in the active case. Stress reversals are of paramount importance for annealing in both.

From an algorithmic standpoint, annealing resembles a search problem for finding progressively deeper minima in the glassy landscape. The activity introduces additional search directions, which are then randomized after a persistence time, enabling the system to explore more of the phase space and attain lower energy states. We demonstrate how this optimization problem can be solved by finding the optimal value of τ_p for the best annealing, given an f₀. Because biological systems experience a plethora of internal and external stresses, we then conduct a detailed study of yielding in active glasses under external loads to understand the emergence of activity-induced rigidity in these systems. We observe early yielding in active glasses and demonstrate how external strain rate couples to the persistence time, resulting in non-monotonic stress responses. This is explained by considering that for faster strain rates, a larger persistence time leads to forces being quenched in non-optimal directions, resulting in the glass yielding via higher energy pathways. We also study how shear bands are affected by active forcing. Shear bands can become unstable at high enough f₀, resulting in a more homogeneous failure. A heterogeneous, shear-band-mediated failure can, however, again be brought back at high enough τ_p. Thus, it is clear that the physics of yielding in active glasses is rich and demands further exploration. Insights provided in this study could help guide the synthesis of bio-inspired smart materials with an internally self-regulated range of softness, for instance, using active gels⁵³.

Compelling future research directions might involve exploring the possibility of encoding multiple memories in the active systems and to find out whether such memories are persistent or not. Stress-controlled oscillatory shearing, which we have explored in some detail (Supplementary Information), has revealed rich new physics. One such phenomenon is normal modes-assisted annealing, which we demonstrate in the Supplementary Information and Supplementary Videos 1 and 2. This needs to be explored further. Another intriguing question is whether there exists an optimal combination of temperature and activity that maximizes annealing efficiency, akin to the optimal shear amplitude and temperature combination reported previously³². Answers to such questions could have consequences ranging from better annealing techniques to better algorithm design.

Model and simulation details

For our MD simulations, we used a well-known model glass former, the binary KA mixture³⁵. It involves two species of particles interacting via Leonard–Jones potential (equation (1)), with the larger A-type and smaller B-type present in a ratio of 80:20:

in which α and β denote the particle types (A or B), and r_ij is the inter-particle distance between the ith and jth particles. The energy and length scales are chosen such that ϵ_AA = 1 and σ_AA = 1. The interactions between the other combinations of particles are then given in terms of ϵ_AA as ϵ_AB = 1.5ϵ_AA and ϵ_BB = 0.5ϵ_AA. Similarly for length scales, we have σ_AB = 0.8σ_AA and σ_BB = 0.88σ_AA. The cutoff range is taken to be 2.5σ_ij, and the potential is made to go to zero smoothly at this point (by choosing u(r_ij) so as to make the slope continuous at the potential cutoff).

For imparting activity, we add an additional force \({{{\bf{f}}}_{0}}\) (equation (2)) to the smaller B-type particles in addition to the potential derived force:

k_x, k_y and k_z can take integer values of ±1. \(\hat{x}\), \(\hat{y}\) and \(\hat{z}\) are unit vectors along corresponding directions. The force is added along the eight diagonal directions, and the directions are shuffled after a persistence time τ_p. This results in run-and-tumble dynamics, and in the literature, it is referred to as the eight-state clock model¹⁹. Momentum conservation is ensured by maintaining the sum of k values to be zero component-wise throughout the simulations. A Nosé–Hoover thermostat and barostat were used to maintain the desired temperatures and pressures.

The typical system size considered is N = 10,000, with additional simulations performed for N = 32,000, N = 64,000 and N = 128,000 particles to study systematic finite-size effects. A very low temperature of T = 0.01 is maintained throughout activity-driven annealing and during tensile testing. The first part of the analysis, including yielding and memory studies, was done under periodic boundary conditions. Open boundaries were created for the second part involving tensile testing. All the simulations were conducted using our custom parallel message passing interface (MPI) C codes.

Annealing, tensile testing and memory reading/writing protocols

Initial states

The states for annealing were prepared by cooling a liquid equilibrated at a high temperature of T = 1.0 and high density ρ = N/V = 1.2 to a temperature of 0.01. The cooling rates were varied from \(\dot{T}=1{0}^{-1}\) to \(\dot{T}=1{0}^{-6}\). These resulted in states with inherent state-per-particle energies ranging from −6.910 (poorly annealed) to −7.035 (well annealed). An ensemble average of 16 independent samples are taken for each case.

Annealing protocol

The obtained states, having a range of inherent state energies, are then subjected to local perturbations via active dynamics. The protocol involved imparting activity to all the B-type particles in the system and evolving such a system for 10⁵ time units (or 2 × 10⁷ MD steps) under isothermal conditions at a low temperature of T = 0.01 (except for the point at f₀ = 1.9 for the lowest energy curve, which was run for twice as long to better gauge the yielding point). Thus, the system was left to age in the presence of various magnitudes of active forcing (f₀), and the resulting states were then used to perform tensile testing.

Energy minimization protocol

To understand where in the energy landscape the system is during the annealing process, we sampled states at equal intervals from the isothermal ageing trajectory and performed energy minimization using the well-known conjugate gradient method. The final energies plotted in the yielding diagrams in Fig. 1b,c are the average energies calculated from a very short time window from the tail end of the energy-minimized trajectories.

Tensile testing protocol

To perform tensile testing, we utilized the various annealed states and subjected them to 200,000 MD steps under zero-pressure conditions. This step was crucial to prevent any pressure shock when transitioning from periodic to open-boundary conditions. Subsequently, we created two walls of width 2.5σ_AA by freezing the particles’ degrees of freedom along the two faces of the containing box (along the x direction). Open-boundary conditions were created along the other two directions. This configuration was run for an additional 200,000 MD steps to allow the surface to ‘settle in’ before applying a constant strain rate, denoted by \(\dot{\gamma }\), to the walls in opposing and outward directions. This application induced tension in the system, and we studied the system’s response to this tension. The system was pulled until complete failure.

Memory reading/writing protocol

Training involves evolving a poorly annealed sample under activity having the target forcing amplitude(\({f}_{0}^{\;\rm{train}}\)) that needs to be encoded. ‘Parallel reading’ involves creating multiple copies of the sample to be read and evolving them separately, each under progressively larger active forcing amplitude (ideally going up to the yielding amplitude), for a short window of time. Here, we evolve the system for ~50 time units. With τ = 4, this amounts to ~6 active cycles as defined in the text. Average energies during the time window of t = 20 to t = 50 are calculated to estimate the final energy. The absolute value of the difference between the initial and the final energy, averaged over 16 ensembles, is then plotted against f₀ to get the reading.

The dataset for this study is available via Figshare at https://doi.org/10.6084/m9.figshare.27316020 (ref. ⁵⁴).

The code used in this study is available via Figshare at https://doi.org/10.6084/m9.figshare.27316020 (ref. ⁵⁴).

References

Authors and Affiliations

1. Tata Institute of Fundamental Research, Serilingampally Mandal, Ranga Reddy District, Hyderabad, India

   Rishabh Sharma & Smarajit Karmakar

Contributions

R.S. and S.K. conceived the project. S.K. supervised the project. R.S. performed the research and simulations. R.S. and S.K. designed analysis methods. R.S. performed all the analyses. R.S. and S.K. wrote the paper jointly.

Corresponding author

Correspondence to Smarajit Karmakar.

Competing interests

The authors declare no competing interests.

Peer review information

Nature Physics thanks the anonymous reviewer(s) for their contribution to the peer review of this work.

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions