Do Language Models Use Their Depth Efficiently?
Authors: Róbert Csordás, Christopher D. Manning, Christopher Potts
Paper: https://arxiv.org/abs/2505.13898
Code: https://github.com/robertcsordas/llm_effective_depth
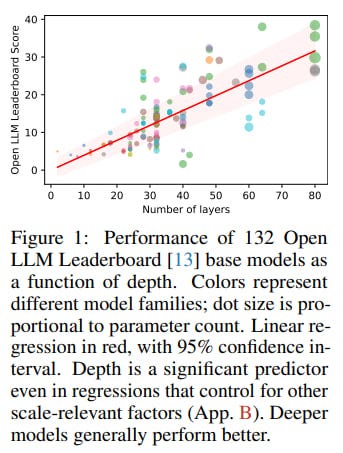
The race for bigger and supposedly better Large Language Models (LLMs) has often followed a simple mantra: more layers equal more power. The underlying belief is that a deeper network allows for more intricate, layered computations, paving the way for models that can conquer increasingly complex reasoning.
However, a fascinating new paper from Róbert Csordás, Christopher D. Manning, and Christopher Potts at Stanford University, titled "Do Language Models Use Their Depth Efficiently?," takes a hard look at this assumption. Their findings suggest that LLMs might not be using their depth for progressively deeper thought, but rather spreading similar computations across their many layers – a conclusion with hefty implications for the future of AI.
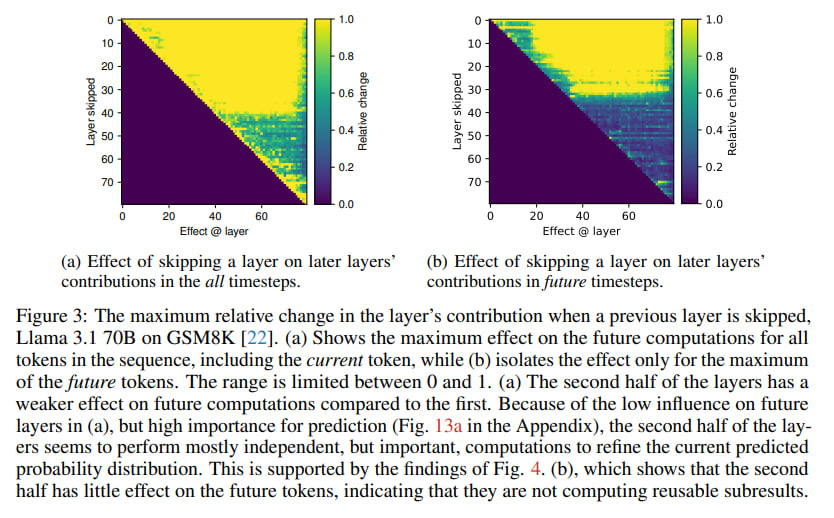
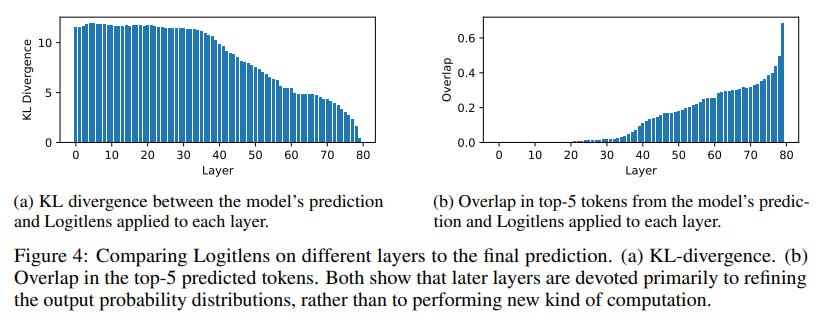
The researchers empirically demonstrate that in prominent models like Llama 3.1 and Qwen 3, the real computational effort seems concentrated in the first half of the network. They found that layers in the second half contribute far less to the model's internal state (the residual stream) and that even skipping these later layers often has a surprisingly small effect on subsequent calculations and the final output. This challenges the prevailing notion that depth inherently enables more complex, compositional reasoning. Instead, it appears later layers are largely busy fine-tuning the output probability distribution, rather than forging new computational paths or building hierarchically on earlier results.
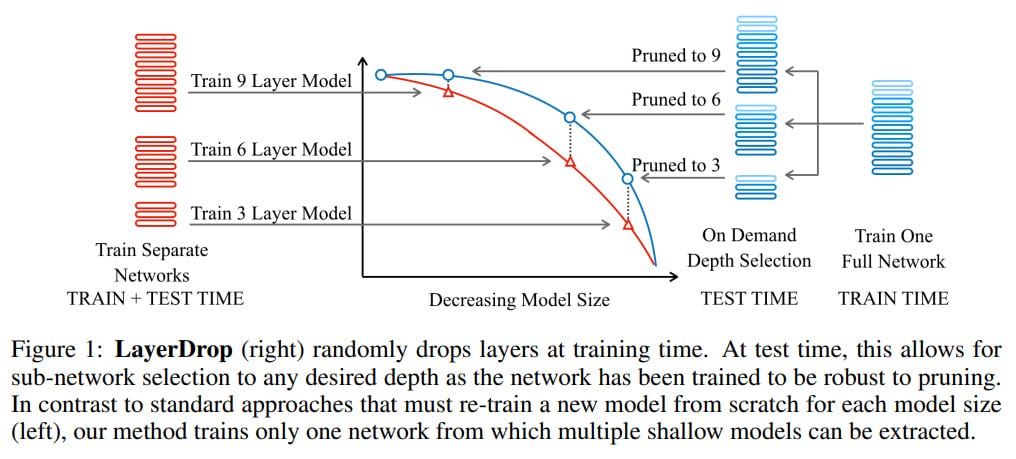
This insight resonates with a growing body of work questioning straightforward scaling, including my own explorations into layer skipping where I found that indeed, not all layers are equal.
The paper's findings also build on prior research that has noted robustness to layer skipping (like "The Remarkable Robustness of LLMs: Stages of Inference?" by Lad et al., 2024) and reordering (as seen in the LayerShuffle concept I reviewed), suggesting a degree of functional redundancy or distributed computation across layers.
LayerShuffle
LayerShuffle: Enhancing Robustness in Vision Transformers by Randomizing Layer Execution Order
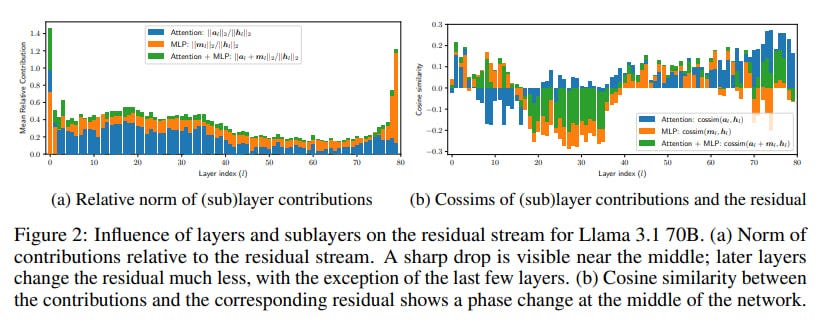
The Stanford team employed a comprehensive suite of causal intervention techniques. For the pre-layernorm Transformers they studied (where sublayer interactions are additive and thus easier to quantify), they analyzed:
L2 norms of sublayer contributions: Measuring how much each layer changes the residual stream.
Cosine similarities: Assessing if a layer writes new features, erases old ones, or refines existing ones.
Layer skipping experiments: Observing the impact of removing layers on downstream computations.
Logitlens: Examining how predictions are refined layer by layer.
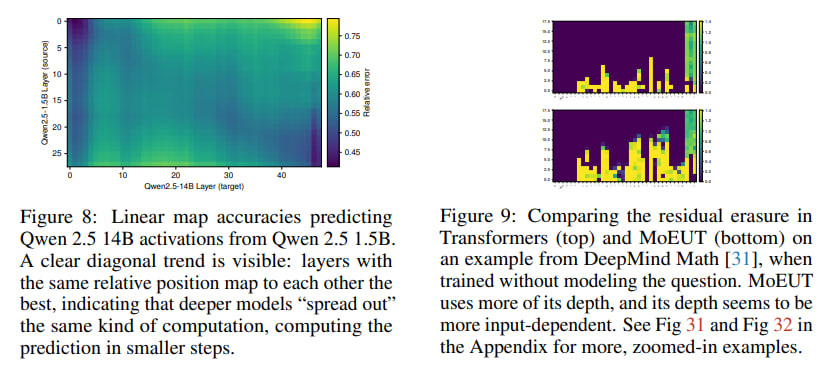
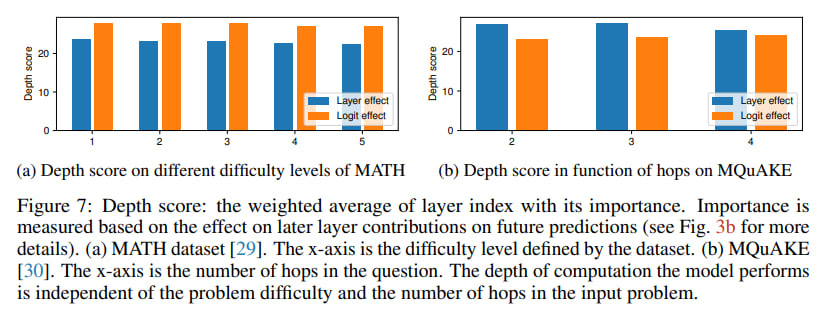
A particularly clever aspect was their focus on tasks demanding compositional reasoning, like complex math problems (GSM8K, MATH datasets) and multi-hop questions (MQuAKE dataset). The logic is sound: if deep compositional reasoning is happening, it should be most apparent here. They even introduced a "Depth Score" metric to see if computational depth scales with problem difficulty and trained linear maps between shallower and deeper models (Qwen 2.5 1.5B and 14B) to test their "stretching out" hypothesis (see Figure 8 below). By the way, I can also see vertical lines here, which reminds me groups of layers I’ve found exploring Gemma 2 internals.
This emphasis on causal interventions provides a much richer understanding of what layers do, rather than just observing correlations.
The results are striking in their consistency. Across different models and tasks, a "phase transition" emerged: the first half of the layers are vital, making substantial contributions. The second half? A significant drop-off in both contribution and impact on future token predictions.
Even when faced with tough math or multi-step reasoning, the models didn't seem to dig deeper into their layers. The "Depth Score" stubbornly refused to correlate with problem complexity or the number of reasoning hops required.
The linear mapping experiment was especially telling: layers in the deeper Qwen 2.5 14B model best corresponded to layers at the same relative depth in its shallower 1.5B counterpart. This strongly suggests the deeper model isn't learning entirely new functions but rather spreading similar computations more thinly across more layers.
These findings could reshape how we think about LLM scaling. If later layers aren't pulling their weight in terms of novel computation, simply piling on more depth might lead to diminishing returns in true reasoning ability much faster than we thought.
This opens exciting avenues for:
More efficient architectures: Perhaps shallower models that are just as capable, or models that can dynamically prune or bypass redundant layers during inference. By the way, see my old series of posts on Adaptive Computation Time.
Conditional computation: The work hints at the potential of mechanisms like Mixture-of-Experts (MoE), which the authors briefly explored and found potentially more depth-efficient (see Figure 9 above).
Understanding reasoning: For those of us working with Chain-of-Thought prompting or other explicit reasoning systems, these findings might explain why externalizing reasoning steps is so effective. If the models don't naturally compose deeply internally, guiding them externally becomes paramount.
Interpretability: Different analytical tools might be needed for early layers (focused on feature integration) versus late layers (focused on refinement). If later layers are primarily refining, as this paper suggests, it's reminiscent of the "Transformer Layers as Painters" idea I discussed previously, where each layer makes incremental adjustments rather than fundamentally new computations.
The authors are upfront about the study's limitations. It's primarily a case study on Llama and Qwen models, so generalizability to all architectures isn't guaranteed. The computationally intensive linear mapping was done on a single model pair. And while the paper shows models don't increase computational depth with problem complexity, the "how" of their problem-solving without this dynamic depth remains an open question.
Future work, they suggest, should dive into these adaptive computation mechanisms and explore architectures and training objectives that can genuinely leverage deep layers more effectively.
This paper is a crucial piece of the puzzle in understanding how LLMs truly operate. It provides compelling evidence that challenges the "deeper is always better for complex reasoning" narrative. The findings strongly suggest that our current architectures might be "longer" in their use of layers, rather than "smarter" by performing qualitatively different, more complex computations in later stages.
It’s a clear call to action for the AI community to investigate beyond sheer scale and focus on designing models that utilize their depth with true compositional efficiency.
P.S. It's worth noting that about 90% of this review was drafted with the help of my experimental multi-agent system designed for analyzing and summarizing research papers. If it might be interesting to you, let me know. I’m thinking of making a web app from it.
.png)