Beating Google's kernelCTF PoW using AVX512 to win $51k

In May 2025, my Crusaders of Rust teammates William Liu (FizzBuzz101) and Savy Dicanosa (Syst3mFailure) discovered and developed an exploit of a use-after-free bug in Linux's packet scheduler. The bugfix patch contains additional details. William found this bug while fuzzing Linux for his master's thesis, which I will link here upon its publication. (Congratulations, William!)

They wanted to submit the bug to Google's kernelCTF competition for an anticipated $51,000 bounty.¹ Unfortunately, finding the bug and writing the exploit was only the first part of the battle. This post documents my small but unique contribution to our ultimately winning the bounty.

To avoid paying out lots of money, kernelCTF organizers limit the number of submissions eligible for a bounty. Every two weeks at noon UTC, the submission window opens. Only the first team who is able to connect to and exploit the server, and submit the flag to a Google Form, receives a payout; any subsequent submissions are marked as duplicates. Furthermore, to prevent excessive submissions, the connecting to kernelCTF server requires solving a "proof of work"—a function which, by design, takes a few seconds to evaluate.

In summary, the submission process has these steps:

1. At 12:00:00 UTC, connect to the kernelCTF server.
2. Solve the proof of work, which takes roughly 4 seconds.
3. Wait for the instance to boot. (Roughly 2.5 seconds.)
4. Upload the exploit and run it to secure the flag. (Time elapsed depends on the exploit. Savy optimized this one to take roughly 0.55 seconds without sacrificing reliability. Wow!)
5. Submit the flag to a Google Form. The submission timestamp determines the winner of the "slot".

Our goal was to complete all these steps in sequence, faster than all the other teams.

Because of the large bounties, over time professional vulnerability research teams have aggressively optimized their submission process. For the May 2, 2025, submission window preceding ours, the first team to submit the flag did so 4.5 seconds after noon!

The numbers don't seem to add up: even assuming an instant exploit and form submission, the VM boot time and proof of work already take 6.5 seconds. Looking closer, we see that the time at which the winning submission's flag was generated (highlighted in red) is one second before noon UTC. Yet, the timestamp is generated after the proof of work is solved. Did sweaty CTFers invent time travel?

Alas! Because of a rounding quirk in the kernelCTF server code (here), the VM instance actually boots at 11:59:59—so no time travel. Still, the timestamp indicates that the winning team solved the proof of work in less than a second! How could this be?

We don't know for certain, but one kernelCTF organizer postulated that they were using field-programmable gate arrays (FPGAs). FPGAs are custom silicon that can perform specific tasks extremely quickly, to the exclusion of general-purpose tasks. They are not only fairly expensive, but also tricky to program. If the professional team had access to an FPGA programmed to perform the proof of work, a sub-second proof of work time was conceivable.

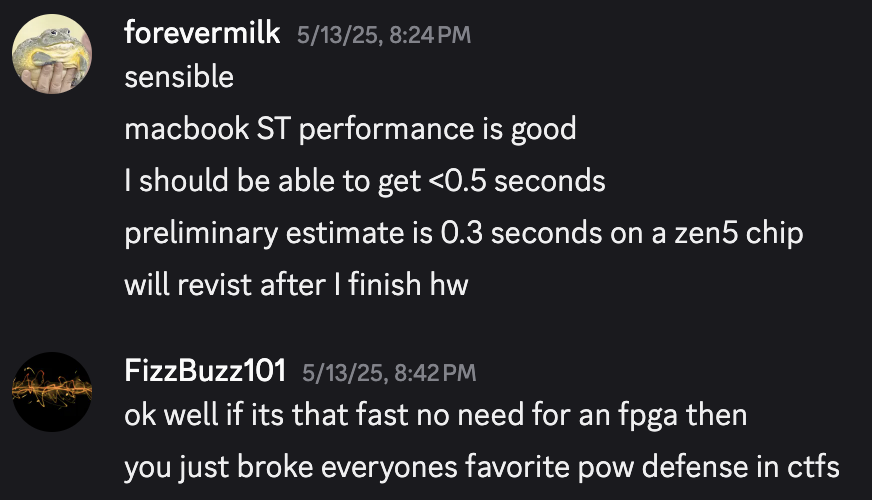
On May 13, William messaged me on Discord seeking advice on how to optimize the proof of work so that we could preempt the competition. I had to act fast: The next submission window would open at 5 a.m. PST, May 16.

The proof of work (implemented here) is a certain verifiable delay function (VDF) known as "sloth". VDFs are cryptographic primitives which prove that a nontrivial amount of time has passed by requiring a long, serial computation. This computation outputs a proof which can be (relatively) quickly verified. Because the computation is serial, scaling to more computational resources (such as more CPU or GPU cores) does not reduce the runtime.²

The sloth VDF was introduced by Lenstra and Wesolowski (2015). I won't reproduce the number theory behind sloth (see page 4 of the paper for that), but to summarize matters, the function we must optimize boils down to:

where x is a supplied 1280-bit integer. The difficulty variable linearly controls how long the VDF takes to solve.

Google's reference implementation uses gmpy, which is a Python binding to the venerable GNU Multiprecision Library (GMP). GMP's addition and multiplication kernels are handwritten in assembly for each target platform (example). The loop-carried dependency of x means that the computation is inherently serial, so throwing more cores at the problem—at least in a naïve way—is unhelpful. Meaningfully speeding up this function was going to be tough.

I set out on the obvious goal of optimizing the 1280-bit modular squaring (line 4 in the code above). The first success was mathematical: Because the modulus is a Mersenne number of length 1279 bits, and the intermediate product is 2 · 1280 = 2560 bits, computing the residue actually corresponds to a handful of cheaper operations:

I also translated the function to C++ to remove FFI overhead. The newly optimized code:

This code ran in 1.9 seconds on my M1 Macbook Pro—a substantial improvement, and faster than similarly optimized solvers like this one written in Rust.³ William linked GMP statically, which would presumably allow some inlining, and reported a further speedup—roughly 1.4 seconds on a fancy Intel Ice Lake laptop. Not bad, but still not a guaranteed win.

The modulus no longer being a bottleneck, I considered handwriting multiplication kernels in assembly to take advantage of the multiplication being a fixed width of 1280-bit × 1280-bit → 2560-bit; the factors fit neatly into twenty 64-bit limbs, and the product fits in forty limbs.⁴ GMP's assembly kernels are generic in the bitwidth, which introduces some overhead. Unfortunately, at 1.4 seconds we were approaching the theoretical limit of multiplication throughput, which is one 64-bit × 64-bit → 128-bit multiplication per cycle on all recent hardware.⁵

AVX512 is Intel's extension to the x86 ISA, first made available in 2016. It is a comprehensive overhaul of x86 SIMD programming, doubling the number and width of vector registers, adding Scalable Vector Extension–style mask predication, and hundreds of new instructions. It also has a troubled history: Linus Torvalds famously wished it to "die a horrible death", and despite supporting it on consumer CPUs for several generations, Intel disabled support for it starting with the Alder Lake µarch (2021); support continues in the server space. Meanwhile, AMD implemented AVX512 in their Zen 4 (2022) and Zen 5 µarches for both consumer and server CPUs.

Of present interest is the AVX512 Integer Fused Multiply–Add extension (AVX512IFMA), which was introduced specifically to speed up big-integer arithmetic—see, e.g., Ozturk, Kantecki & Yap (2024). I learned about AVX512IFMA during my competitive programming arc, optimizing submissions for judge.yosupo.jp. The extension introduces two new instructions which operate on vector registers:

• vpmadd52luq – Packed Multiply of Unsigned 52-Bit Unsigned Integers and Add Low 52-Bit Products to 64-Bit Accumulators
• vpmadd52huq – Packed Multiply of Unsigned 52-Bit Unsigned Integers and Add High 52-Bit Products to 64-Bit Accumulators

Essentially, the instructions perform the following operation (assuming the high 12 bits of each element in a and b are zero):

In simpler terms, the instructions perform the low and high halves of a 52 × 52 → 104 multiplication, and accumulate the result into the destination register. At the execution unit level, the instructions reuse the multipliers used for double-precision floating point, and thus don't necessitate much extra silicon. They also have fantastic throughput: on Zen 5, which has a full 512-bit datapath, we can execute two of these instructions per clock!

At this point I was confident that I could make an extraordinarily fast VDF solver. All that was left was to implement it in two days....

The natural radix for the AVX512IFMA extensions is 2⁵², i.e. 52-bit limbs stored in 64-bit words, so I let ChatGPT write a simple converter between GMP's representation and the 52-bit representation. We need ⌈1280 / 52⌉ = 25 limbs, which requires four 512-bit "zmm" registers (each register can store eight limbs, so the last register will only store one).

The first step is squaring the integer into a 50-limb intermediate product. We use a simple symmetry to almost halve the number of required multiplications, breaking up the desired value into two terms:

(a₂₄2^52·24 + a₂₃2^52·23 + ... + a₀)² = (a₂₄²2^52·48 + a₂₃²2^52·46 + ... + a₀²) + 2 i,j≤24∑i=0,j>ia_ia_j 2^{52·(i + j)}

Each of the yellow-highlighted multiplications produces a low term (furnished by vpmadd52luq) and a high term (furnished by vpmadd52huq).

First consider the second term above, the double summation highlighted in red. We want to reduce the number of shuffles necessary to get all the terms in the correct place, and use the "free" 64-bit accumulation as much as possible. One way to do this is to multiply a sliding window of 8 contiguous limbs by a single multiplier limb; all the output words, for both the low and high halves, will also be contiguous in the output. We can also use the merge masking feature to prevent accumulation of products that shouldn't be in the final sum, e.g., pairs where i = j. By selecting these windows and multipliers correctly, we can minimize the number of wasted multiplications.

As an example, accumulator accum[1] contains output limbs 8 through 15, inclusive, and the following accumulations are executed (in this order):

Here, window i contains limbs i through i+7 inclusive. Note that the masks mostly contain ones, indicating that we are not wasting too much multiplication throughput on masked-out elements.

Computing the first term is easier. We just square each element and interleave the low and high words:

Finally, we need to implement the reduction modulo 2¹²⁷⁹-1. This is just a matter of selecting the upper 1279 bits and adding them to the lower 1279 bits. It's worth noting that at this point, the accumulator elements may exceed 2⁵²-1, but we can delay carry propagation until after the addition.

We then need to subtract the Mersenne modulus if the addition is too large, but this is easy to check: we perform the subtraction iff the 1280th bit is 1. Subtracting 2¹²⁷⁹-1 is equivalent to subtracting 2¹²⁷⁹ (i.e., zeroing the 1280th bit) followed by adding 1 to the least-significant limb. Because the subtraction occurs with 50% probability, we do it in a branchless manner:

There is a tiny chance that an overflow occurs in this last step: if the last limb happened to be exactly 2⁵²-1, then we'd need to propagate the carry. However, because PoWs are randomly generated, the probability this happens on any given run is about 2 in a billion—so I just ignored it.

At this point, the PoW was taking about 0.45 seconds on a rented Ryzen 9950X, which is a fast Zen 5 chip. Very promising!

The multiply–add instructions have a latency of 4 cycles, and 2 can start every cycle. Thus, we need at least eight accumulators to fully saturate the multipliers instead of bottlenecking on latency, but we only have seven (and some of them are only used occasionally). The solution is to have fourteen accumulators—one set for the low halves and one set for the high halves—then merge them at the end:

This brought the PoW down to roughly 0.32 seconds. The expanded AVX512 register file, with 32 zmm registers, came in clutch here.

Inspecting the assembly revealed that both GCC and clang were unrolling the loop, converting the _mm512_set1_epi64 instructions into vbroadcastsd zmm, m64 instructions—one per limb—and then running out of vector registers during regalloc. Instead of rematerializing the values, they would stack-spill and reload the broadcasted vectors, causing considerable overhead.⁶

My solution was to use inline assembly to force the vpmadd52luq/vpmadd52huq instructions to use a memory broadcast operand for the multiplier limb. Instructions encoded with such an operand copy a single 32- or 64-bit element from memory to all elements of a vector operand, without consuming an architectural register. Moreover, this broadcast load does not consume any vector ALU resources: it is handled entirely by the load unit!

Now that we're using asm, the compiler can't remove masks of all 1s, so for optimal encoding we need separate asm for the all 1s case. Finally, when the multiplier limb happens to be at index zero in one of the zmm registers (i.e., multiples of 8), we use vpbroadcastq to splat it from register to register, which I measured to be a performance improvement over loading it from memory. The accumulation sequence is now:

(This is just for the low set of accumulators; the high set is nearly identical.) At this point, the PoW was taking roughly 0.23 seconds.

To compute the "windows", we are storing the integer to memory in an aligned fashion, then loading from it in an unaligned fashion. This is a classic situation that causes a store-forwarding stall, which further lengthens the critical path (the multiplications cannot commence until a window is loaded from memory). A better solution is to use the valignq instruction, which lets us simulate an unaligned load from the clumps array containing our integer.

This brought the PoW down to 0.21 seconds. At this point, I decided to call it quits and sent my teammates the final C code.

My friends got up at 4:30 a.m. PST, May 16, to prepare for the final submission; I couldn't be assed to be awake, so I slept until 6:30. They spun up a Zen 5 Google Cloud server in the Netherlands, geographically closest to the Google Form submission server, to minimize latency. A few minutes before 5:00, they recorded an intercepted POST request submitting the Google form, but with a dummy flag. The form submission program was devised and optimized by Bryce Casaje (strellic) and Larry Yuan (ehhthing). Max Cai also assisted in development and submission. Then at 5:00, the server connected to the kernelCTF server, solved the proof of work, ran Savy's optimized exploit, inserted the flag into the POST request, and sent it off....

We got it in 3.6 seconds—the fastest-ever kernelCTF submission! Later that day, the kernelCTF organizers confirmed our eligibility for the bounty and we all breathed a collective sigh of relief. Again, congratulations to Savy and William for discovering and exploiting this bug! Thanks to them for presenting me with the challenge, and thanks to my CSE 260 professor Bryan Chin (website) for what he taught us about program optimization.

On May 28, kernelCTF organizer koczkatamas announced that the proof of work was being removed:

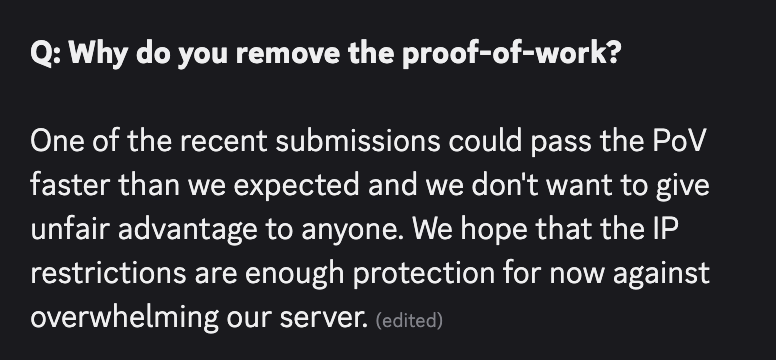
On the one hand, it's sad that we no longer have a competitive advantage, and the slot race becomes purely about exploit duration and network latency. On the other hand, at least people don't need to buy expensive FPGAs, or pull out their inline asm knowledge, to be on equal footing with the professionals. It also frees me to release this post!

Please message me on Discord (@forevermilk) if you have any comments or questions. I am also researching VDFs that are more resilient to assembly-level optimizations; if you have any ideas or would like to collaborate, I'm all ears.

This code is the product (ha!) of about 12 hours of work across May 14 and 15, and it is correspondingly unclean. Consider it released under the GNU AGPL 3.0.

I hope you enjoyed my first-ever blog post. Hopefully there will be many more.