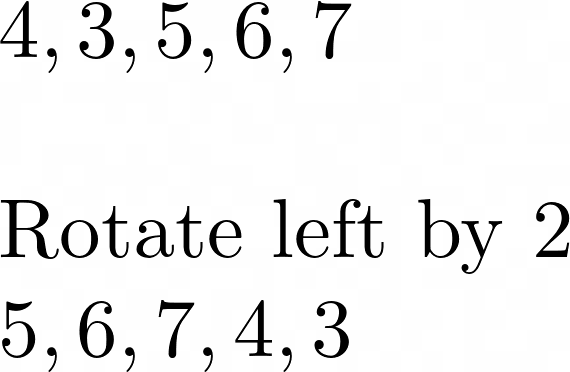Building a Catalytic Computer over the Weekend

3 days ago 3

Quick intro

LeetArxiv is Leetcode for implementing Arxiv and other research papers.

Catalytic computing algorithms are somewhat fascinating. They permit computations using memory-occupied by other processes.

Think of it this way :

You have both Chrome and VS Code running, they both consume lots of memory, and so your computer gets slow.
Theoretically, a catalytic space algorithm would permit VS Code to borrow memory from chrome.
That is, VS Code would be able to use Chrome’s allocated memory to perform computations (all while Chrome is running) and with zero change to Chrome’s internal state.

In practice, computations in catalytic space are rather slow. Too slow to make this computational paradigm useful. Nonetheless, the concept is interesting and so, we shall implement the original 2014 paper, Computing with a Full Memory : Catalytic Space, by Buhrman et al.

This section summarizes the introduction and preliminaries section of Buhrman et al.

I must admit, the paper is full of dense complexity-theory jargon.

The authors introduce the idea of a catalytic Turing machine.
- A regular Turing machine has 3 tapes: input, output and work tapes while a catalytic Turing machine has 4 tapes : input, output, work and an auxilliary tape.
- A Turing machine is said to be catalytic if the auxilliary tape remains unchanged after computation.
CSPACE is defined as the class of sets that can be computed by catalytic computers.
- Inside CSPACE, TC is a class of binary functions that can be computed by a catalytic computer. These include AND, OR and Majority which we encountered here.

The mathematical set of permutations, also known as the Symmetric Group, is fundamental to catalytic computing.

Buhrman et al. builds upon two papers we already implemented here on LeetArxiv:

This paper tells us that we can simulate complex binary operations using simple rotations and permutations.

This paper introduces Reversible Computing : a computational paradigm that lets one start from an output and go back to the original input.

We can dive into the concept of transparent computations since we already implemented the papers above.

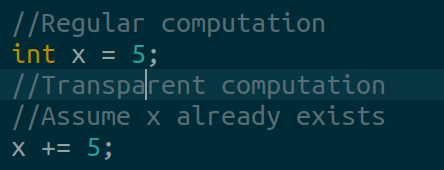
A transparent computation is a computation that adds a result to an existing variable.

In a regular computation, one declares a variable and assigns a value to the variable’s memory location.

However, in a transparent computation, one assumes the memory already exists. Therefore, one assigns a value to the existing memory location by addition.

In this section, we focus on building addition, multiplication and comparison operations for our catalytic computer.

Remember, we’re working in the symmetric group so we can use the group’s basic operations, rotations and reflections, to implement catalytic arithmetic.

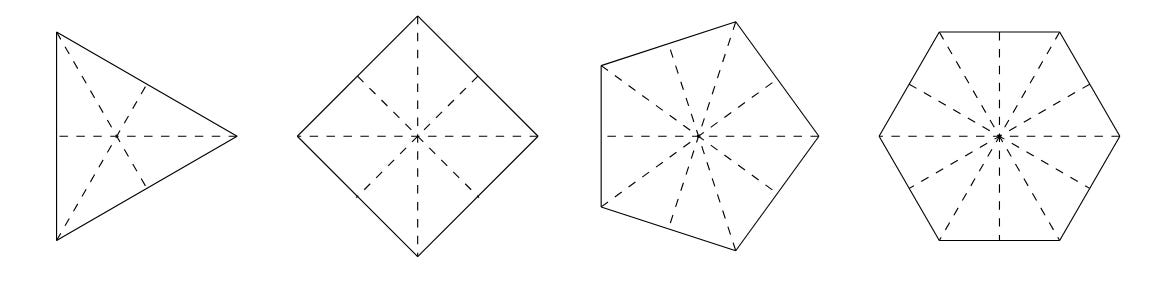
The dihedral group, D_n, is defined as the rigid motions* taking a regular n-gon back to itself.

*Rigid motions are stuff like rotations, reflections and translations

*n-gon is math-jargon for polygons (stuff like triangles, squares, pentagons etc)

Also, in our earlier discussion here, we observed that catalytic computers exist within the alternating group, the set of even permutations. This means we can build a catalytic computer within the dihedral group but only if we restrict ourselves to rotations and avoid reflections.

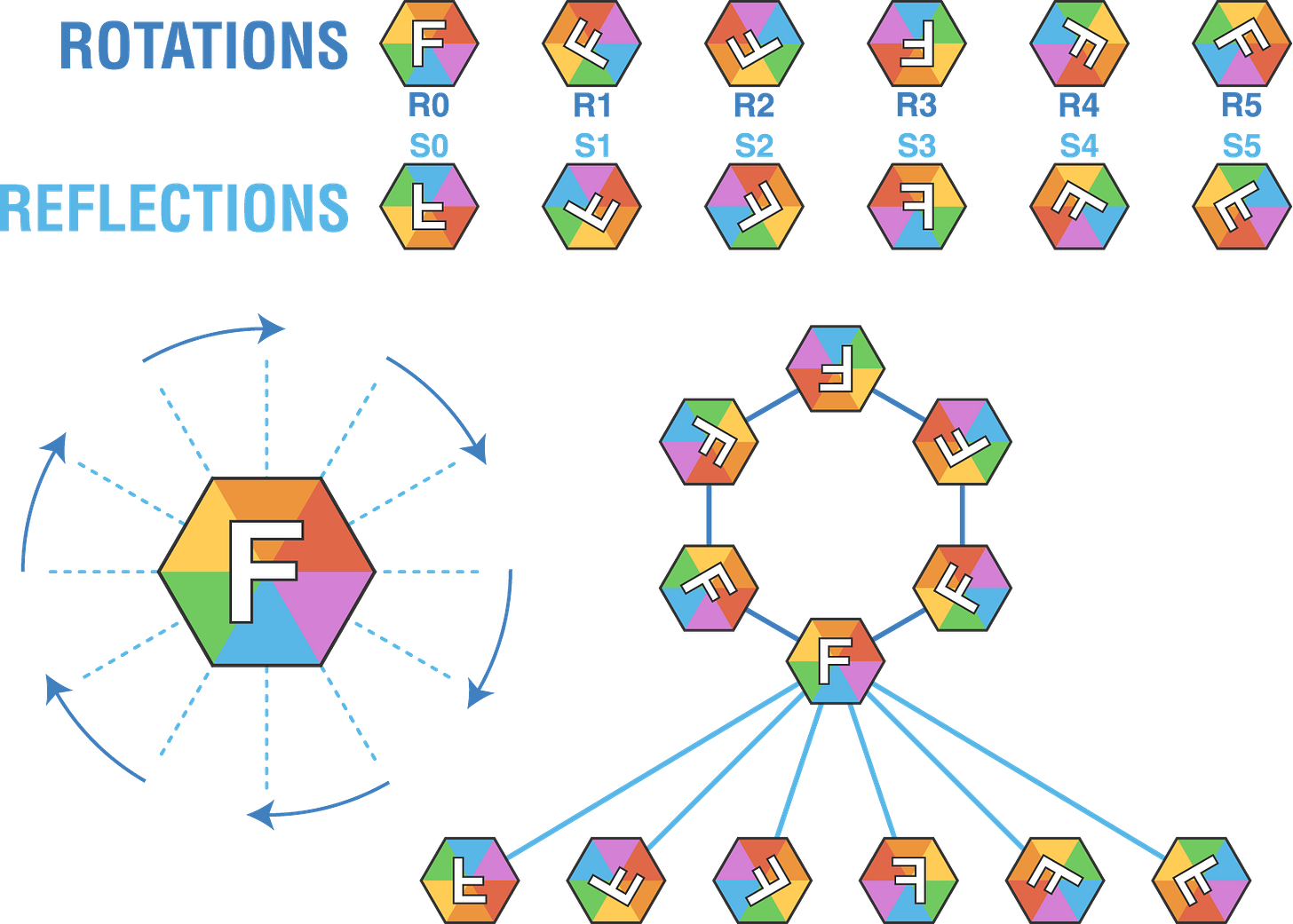
The paper doesn’t exactly tell us what we need to be rotating. Therefore, I’ll provide two possible interpretations:

According to Cook’s interpretation rotating the elements of an array horizontally achieves addition. Here’s a rotation example ;

I bet a right rotation would be valid as well. Again the original paper authors didn’t provide code so we’re mostly f’ing around and finding out :)

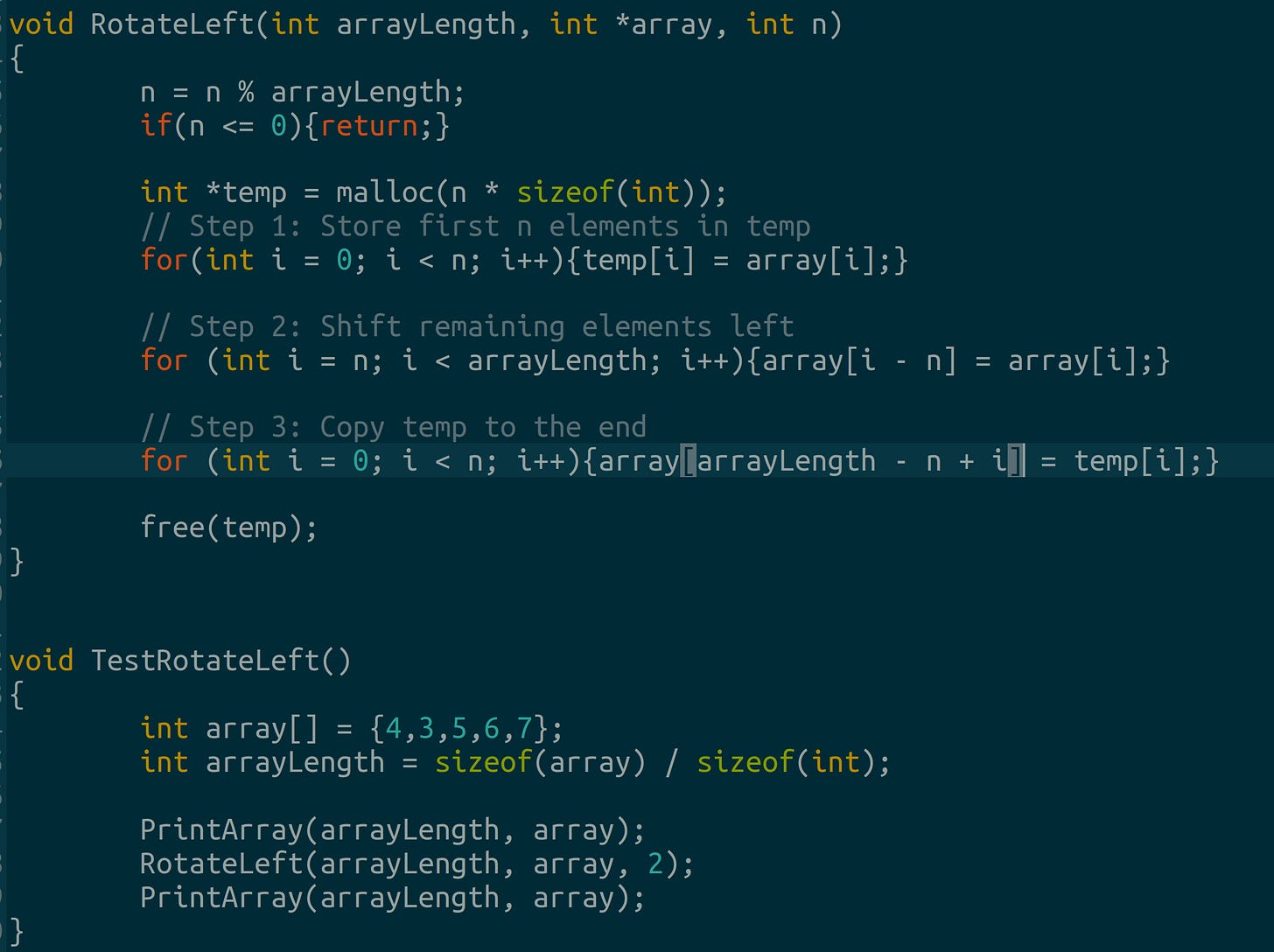
We can implement this in C. We use a temporary array to hold intermediate results. You can implement rotations much more efficiently if you want.

Since the paper is ‘free-to-interpret’ we can also try to see if modular arithmetic can be used instead of array shifting.

We’ve been working a lot with modular arithmetic and residue number systems in our, What Every Programmer Needs to Know about Finite Fields series and so, we already have a number system that encodes rotations.

Therefore, we’ll borrow (rather heavily) from the RNS conversion code we wrote here.

The authors introduce a 5 step multiplication algorithm on page 7. The operation is somewhat convoluted because (if you remember) transparent computations must be reversible.

Also, we dedicated an entire section here to understanding the standard basis, as mentioned by authors in the screenshot above. So, we can jump straight into the implementation.

Cited as

Kibicho, Murage. (June 2025). Building a Catalytic Computer Over the Weekend. LeetArxiv. https://leetarxiv.substack.com/p/catalytic-computer

@article{Kibicho2025BuildingaCatalyticComputerOvertheWeekend, title = "Building a Catalytic Computer Over the Weekend.", author = "Kibicho, Murage", journal = "LeetArxiv", year = "2025", month = "June", url = "https://leetarxiv.substack.com/p/catalytic-computer" }