Cavity quantum electrodynamics with moiré photonic crystal nanocavity

Cavity quantum electrodynamics (CQED) explores the fundamental aspects of interactions between quantum emitters and light trapped in a cavity, which is primarily discussed in the strong and weak coupling regime^1,2,3,4,5. In the weak coupling regime, local density of optical states in the cavity will modify the radiation characteristics of quantum emitters, called Purcell effect, which facilitates the realization of high-efficiency quantum light sources^6,7,8,9,10 and ultra-low-threshold lasing^11,12,13,14. In the strong coupling regime, where the coupling strength exceeds the system loss rate, coherent energy exchange between light and the quantum emitter occurs, enabling applications in quantum information transfer^15,16,17,18 and nonlinear quantum optics^19,20,21,22. Therefore, research on CQED is vital to the development of quantum information technology. Self-assembled quantum dots (QDs), well known for high qualities in brightness, purity, and indistinguishability for single-photon emission, flexible controllability, and easy integrability into optical structures^23,24,25, are one of the most promising solid-state quantum emitters for realizing quantum information technology^26,27. For experimentally studying CQED, the microcavity is expected to have a high quality factor (Q) and a small mode volume (V) to guarantee a large coupling strength between the single QD and the light. So far the coupling between a single QD and a microcavity in both weak and strong coupling regimes has been experimentally realized in different optical platforms, such as whispering-gallery-mode microcavities^28,29, photonic crystal cavities and waveguides^30,31,32,33, and distributed Bragg reflector cavities^34,35,36. Though benefiting from those traditional cavities with a relatively high Q/V, the value of Q/V so far is still one of the main restrictions of further developing quantum information technology.

Recently, moiré photonic crystal (MPhC) nanocavities provide a new paradigm for CQED study with a high Q/V^37,38. MPhC superlattice is a counterpart of the moiré electronic systems^39,40,41 in terms of photonics, which is formed by the interlayer interaction of two identical photonic graphene lattices twisted at a given twist angle^{37,38,42,43,44,45,46,47,48,49,50,51,52,53,54}. The coupling of Bloch modes between the bilayer lattices gives rise to the formation of flatbands in the energy band. The flatbands enable momentum-independent light confinement of Bloch waves and result in modes with zero group velocity, which lead to a high Q and ultra-low V for MPhC nanocavities. Therefore, each unit cell serves as a nanocavity where light can be highly confined. MPhC devices such as moiré lasers^37,38,45 have been demonstrated recently. However, the coupling of a moiré nanocavity with a single QD has not been studied experimentally, which can be attributed to two reasons. The first one is that a suspended bilayer twisting structure that matches QDs in the near-infrared regime is very easy to collapse during fabrication, suffering from the limited GaAs used to support the structure. The second one is that the nanocavity mode field is predominantly distributed in the air holes, hindering the effective spatial overlap between the QD and mode field for a large cavity-QD coupling. Therefore, to take advantage of the MPhC for further study on CQED, these two problems remain to be solved.

This work reports on the weak coupling between the MPhC nanocavity modes with single QDs. We optimize the Q and the effective area to place QDs by varying the filling ratio of the single-layer photonic crystal through numerical simulation. A theoretical Q of 10⁵ is obtained, and the effective area is increased by ~35%. We then design and fabricate the MPhC nanocavities onto a one-layer GaAs slab with QDs embedded. The experimental Q is ~2000. When a single QD resonates with the fundamental mode, its luminescence intensity is enhanced by a factor of ~8.4. The emission rate measured from the lifetime is enhanced by a Purcell factor of ~3, and the single-photon purity measured from second-order correlation exhibits a twofold improvement. These results pave the way for realizing high-quality single-photon sources based on MPhC nanocavities, which offer a promising platform to advance the development of quantum information processing and CQED exploration.

Design and optimization of moiré superlattice structures

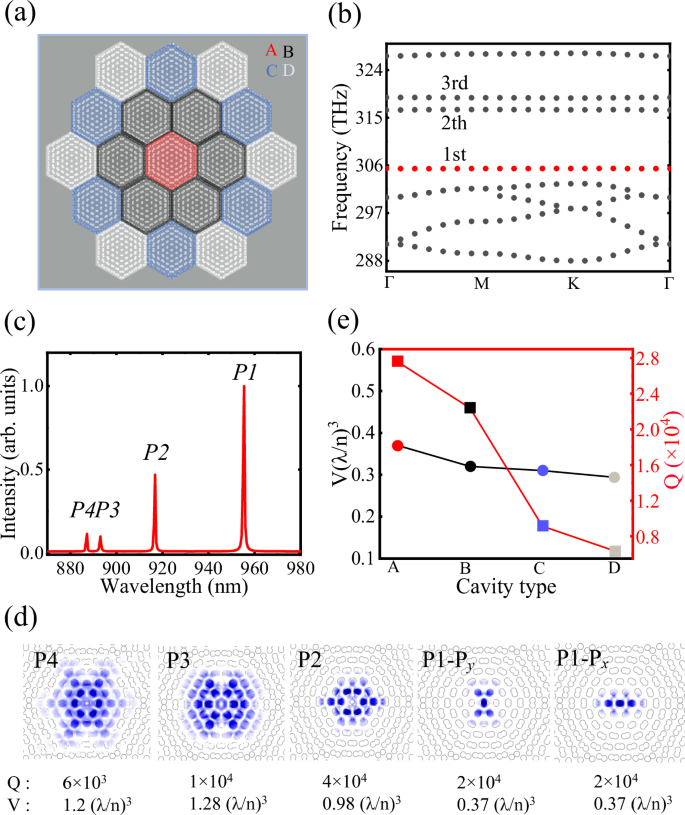
The MPhC superlattice is composed of two layers of photonic crystals twisted at a specific angle. As the twist angle decreases, the size of the unit cell of the superlattice increases³⁷. However, the field distribution of fundamental modes remains essentially the same³⁷. The Q/V ratio of fundamental modes of the MPhC nanocavity increases sharply as the twist angle decreases. It is worth noting that an MPhC nanocavity with Q factor exceeding 1 million has been demonstrated recently at a small twist angle⁴². A smaller twist angle results in a higher Q factor, but the resonance wavelength of MPhC nanocavity redshifts. It requires smaller lattice constants and airhole radii for resonance with QDs, which makes the device more difficult to fabricate. Generally, a trade-off must be made between fabrication feasibility, the twist angle, and the number of moiré layers. To match the photoluminescence (PL) of the QDs, we designed the MPhC superlattice with a twist angle of 6.01°, as shown in Fig. 1a. The design principle of MPhC nanocavities is discussed in Supplementary Note 1. The fabricated moiré superlattices are finite in size, resulting in different surrounding environments for each unit cell. Therefore, the superlattice is divided into four types of nanocavities with different spatial equivalence, which are marked in red (A), black (B), blue (C), and gray (D) in Fig. 1a, respectively. Figure 1b depicts the band structure of the twisted nanocavity calculated by the time-domain finite-difference method where the lattice constant of the single-layer photonic crystal a is 302 nm, the radius of the airhole r (0.238a) is 72 nm. The red dots in the bandgap show the band of orthogonal degenerate fundamental (1st) modes. Other higher-order (2nd, 3rd) modes also appear in the bandgap. Figure 1c shows the spectrum of the nanocavity obtained from the simulation, where P1 are the orthogonal degenerate fundamental modes, and P2-P4 are the higher-order modes. The corresponding field distributions as well as Q, V are shown in Fig. 1d. The fundamental modes have both high Q and ultra-low V. Although the higher-order modes have high Q but a relatively larger V, therefore, we take advantage of the fundamental modes to study CQED. Figure 1e shows the Q and V of the four different types of cavities from the same moiré superlattice structure. The Q of fundamental modes from cavities A and B are higher than those from cavities C and D, while their V do not show a big difference, ~0.35(λ/n)³.

Fig. 1: Structure and cavity mode properties of MPhC superlattices.

a Schematic of the MPhC superlattice. A, B, C, and D represent different types of cavities marked in different colors. b Band structure of the twisted nanocavity with a lattice constant of a = 302 nm and radius of r = 72 nm. c The spectrum of different cavity modes labeled by P1–P4 of the nanocavity obtained from the simulation. d The corresponding field distributions, Q and V of different modes corresponding to (c), where P_x and P_y are the orthogonal degenerate fundamental modes. e The theoretical Q and theoretical V of fundamental modes for different types of nanocavities.

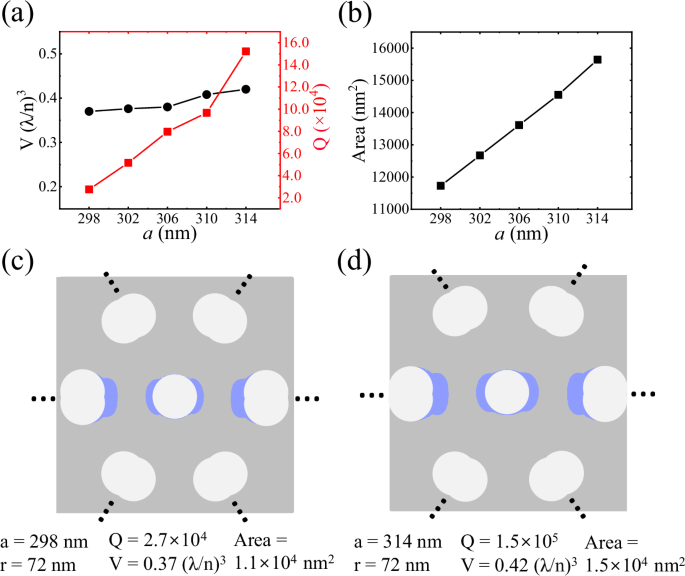
To observe the effective coupling of QDs with MPhC nanocavities experimentally, we optimize the Q and the effective area of the fundamental modes, focusing on cavity A. The effective area is defined as the region within GaAs where the electric field strength exceeds half of the maximum field strength. The Q and the effective area are optimized by tuning the lattice constants a and simultaneously fixing the hole radius r of the single-layer photonic crystal slab, which means the filling ratio is changed, as shown in Fig. 2a, b. In Fig. 2a, the black and red lines represent the theoretical V and Q of the fundamental modes for different a values. With r fixed at 72 nm, the Q increases as a increases, while V remains ~0.39(λ/n)³. When a = 314 nm, the Q of the fundamental modes can reach 10⁵. In Fig. 2b, the effective area increases from 11,500 nm² to 15,500 nm² as a increases, with an improvement of ~35% for the P_x fundamental mode. Figure 2c, d shows the mode profile of the effective area for the P_x mode when a is 298 nm and 314 nm, respectively. The effective area of the P_x mode is noticeably larger for a = 314 nm compared to a = 298 nm, thereby enabling a larger possibility to achieve QD-cavity coupling. The optimization for P_y mode is described in Supplementary Note 2. Optimizing the effective area of MPhC nanocavity is a major direction for the future. Our work offers valuable insights for other researchers to develop applications based on these high Q/V nanocavities. The increase in effective area also allows the position of the QDs to be further away from the GaAs/vacuum interface. Therefore, fewer QDs will be affected by detrimental factors such as surface charge fluctuations⁵⁵.

Fig. 2: Optimization of fundamental modes in moiré nanocavities.

a The theoretical Q and V of fundamental modes for different a. b The effecitve area of P_x fundamental mode with different a. c, d The cavity mode profile of effective area (blue) of P_x fundamental mode when a is 298 nm and 314 nm with r = 72 nm.

PL spectroscopy of moiré nanocavities

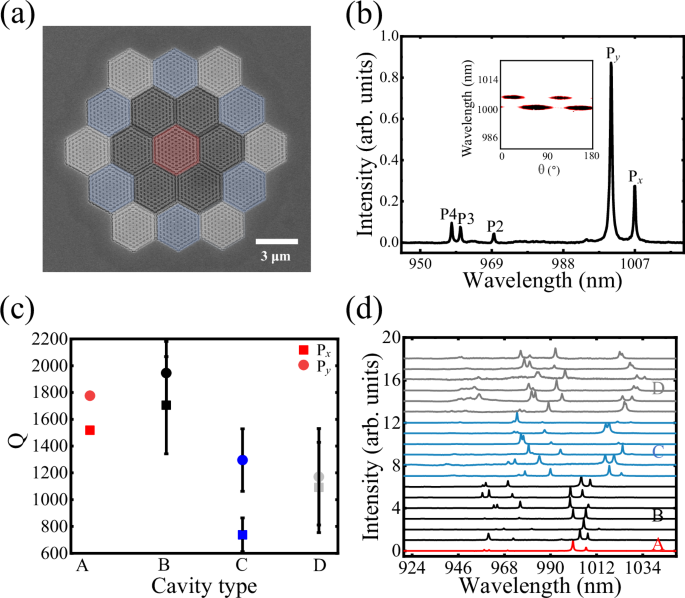
Figure 3a shows the scanning electron microscope (SEM) image of a MPhC nanocavity. The photonic crystal slab with a thickness of 150 nm sandwiches a single-layer of InGaAs QDs in the center, which functions as quantum emitters at near-infrared wavelengths. The structure fabrication process is shown in Supplementary Note 3. To investigate the coupling between single QDs and nanocavities, the density of QDs is required to be low enough, which is less than 10 μm⁻² in this work. The moiré nanocavities are mounted in a liquid helium flow cryostat for the confocal micro-PL measurement. QDs and MPhC nanocavity modes are excited by a 532 nm continuous-wave laser. Even when the cavity mode is detuned from the QDs, photons in the cavity mode are generated by the emission from the ensemble of QDs with the assistance of phonons^56,57. The PL signals are detected by a charged-coupled device camera with a spectral resolution of 60 μeV. The collected PL spectrum from cavity A with a = 310 nm, r = 72 nm, and δd = 4 nm is shown in Fig. 3b. P_x and P_y are the split fundamental modes, and P2, P3, and P4 are the higher-order modes, as shown in Fig. 1c.

Fig. 3: Characterization of MPhC nanocavities.

a SEM image of a MPhC superlattice structure. b The collected PL spectrum from cavity A with a = 310 nm, r = 72 nm, and δd = 4 nm. The inset shows the polarization diagram of fundamental modes. c Average experimental Q of two split peaks from different types of nanocavities of the superlattice structure, where error bars represent the mean deviation. d The experimental PL spectra from different cavities in the same superlattice structure. The spectra are shifted for clarity.

The wavefunctions of the fundamental modes are localized in the center of the nanocavity, spatially separated from the fundamental modes of the surrounding cavities, which ensures independent collection of PL for different types of MPhC nanocavities. The polarization diagram of P_x and P_y modes is shown in the inset of Fig. 3b. The pair of fundamental modes is linearly polarized and orthogonal to each other^37,38,51. The two peaks are theoretically degenerate, but the degeneracy is lifted because the fabricated circular air holes are not ideal with the C₆ symmetry breaking, which is also verified by the numerical simulation, as shown in Supplementary Note 4.

Figure 3c shows Q of P_x and P_y peaks from different spatial types of nanocavities in the moiré superlattice structure. In the experiment, the Qs of two peaks from cavity A and cavity B are similar and twice higher than those from cavity C and D. The collected PL spectra from different cells in the MPhC superlattice structure are shown in Fig. 3d. The spectra of the nanocavities exhibit similar PL peak profiles, but the mode wavelengths of each nanocavity differ, suggesting the existence of slight local differences while maintaining the global bilayer twisted lattice coupling effect.

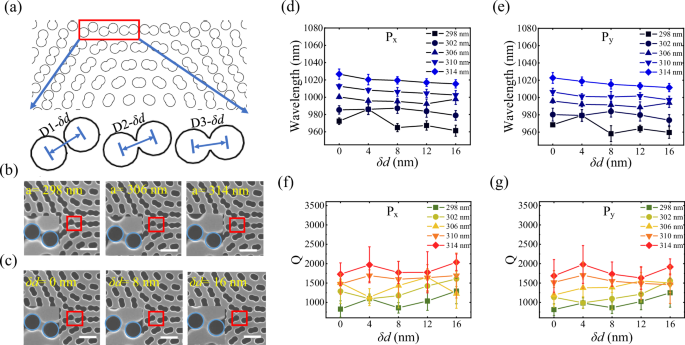
The schematic diagram of the outermost layer of the nanocavity structure is shown in Fig. 4a. Due to the C₆ symmetry of the nanocavity structure, there are three different types of adjacent airhole pairs with spacings labeled as D1, D2, and D3. The outermost air holes of the nanocavity are close to each other due to the rotation configuration of the bilayer photonic crystal. The retained GaAs is not enough to support the entire bilayer twisted photonic crystal structure, making it challenging to fabricate suspended MPhC nanocavities successfully^37,42. To solve the problems, two methods are used to optimize the MPhC structures. One method is to tune the lattice constant of the single-layer photonic crystal, as shown in Fig. 4b. Another method is to reduce the relative distance between each pair of air holes in the outermost layer while maintaining the C₆ symmetry, as shown in Fig. 4c. As the lattice constant a increases from 298 nm to 314 nm or the displacement distance δd increases from 0 nm to 16 nm, the retained GaAs material marked by the red box in Fig. 4b, c increases, so that the outermost layer has more GaAs material to support the entire structure. The experimental results from MPhC superlattice structures with different superlattice period numbers are presented in Supplementary Note 5.

Fig. 4: MPhC nanocavity structure and fundamental mode characteristics with different a and δd.

a The schematic diagram of the outermost layer of the nanocavity structure. b Enlarged SEM images of the outermost layer of the nanocavity structure for different a of the fabricated photonic crystal structures, where the scale bar is 0.4 μm. c Enlarged SEM images of the outermost layer of the nanocavity structure with different displacement distances δd, where the scale bar is 0.4 μm. d, e Average wavelengths of two split fundamental modes for different a and δd, where error bars represent the mean deviation. f, g Average Qs of two split fundamental modes for different a and δd, where error bars represent the mean deviation. All the structures here have air holes with r = 72 nm for the single-layer lattice.

The wavelength and Q fitted through the Lorentz line shape of P_x concerning a and δd are shown in Fig. 4d, f. As a increases, the cavity central wavelength is redshifted, and the Q increases. Take an example, with δd = 0, when a increases from 298 nm to 314 nm, the wavelength is redshifted from 968 nm to 1022 nm, and Q improves from 800 to 1700. As δd increases, the wavelength is blue-shifted. The relation between Q and δd varies according to the lattice constant. When a is small, Q improves as δd increases, e.g., when a = 298 nm, Q improves from 810 to 1300 as δd increases from 0 nm to 16 nm. When a is large, the increase in Q is not obvious as δd increases. When a = 314 nm, δd = 16 nm, Q can reach ~2000. The results for P_y mode with a and δd are similar to those of P_x, as shown in Fig. 4e, g. The simulation results and experimental PL spectra of MPhC nanocavities with varying δd are shown in Supplementary Note 7. We have also investigated the wavelength fluctuations of different MPhC nanocavities of the same cavity type in one superlattice. The mode fluctuations of the fundamental modes are ~6 nm (Supplementary Note 6), which is similar to the fluctuation range of robust topological corner states¹³.

Purcell enhancement of single quantum dots

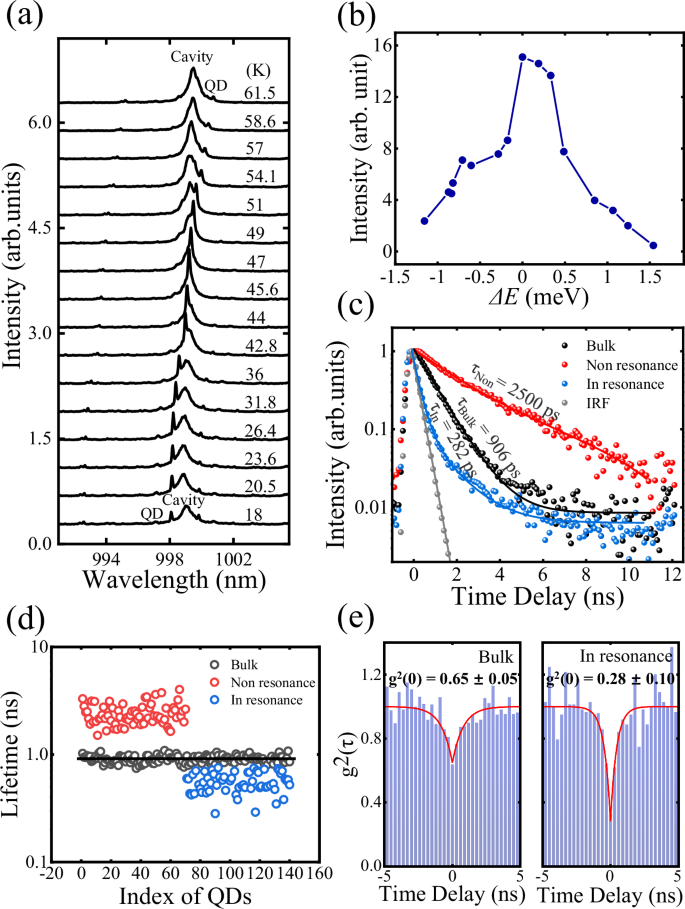
To investigate the interaction between single QD and the nanocavity, we use a low-excitation power of 15 μW to pump the sample so that the QDs and the cavity appear simultaneously on the PL spectrum. Figure 5a shows the PL spectra of the QD crossing the nanocavity fundamental mode by varying the temperature. Figure 5b shows the Lorentz fitting results of the area intensity of the QD in Fig. 5a. As the QD-cavity mode detuning ΔE changes from negative to positive, the area intensity of the QD PL first increases and then decreases. The asymmetry in the QD emission intensity with respect to the QD-cavity mode detuning is the result of ramping up of nonradiative losses, such as the Auger effect and phonon emission^58,59. When ΔE is −1.15 meV, the area intensity of QD is ~1.8. When the QD is in resonance with the cavity mode, the area intensity of QD is ~15.1, indicating the Purcell enhancement for weak coupling between the QD and the cavity. The fitted intensities and wavelength variations with temperature of the QDs corresponding to the spectra in Fig. 5a are presented in Supplementary Note 8. We can see that the area intensity of the QD is enhanced by a factor of ~8.4 when the QD is in resonance with the nanocavity mode. Other typical PL spectra of QDs and MPhC cavity modes at different detunings are presented in Supplementary Note 9.

Fig. 5: Purcell effect and single-photon emission characteristics of single QDs coupled to MPhC nanocavities.

a PL spectra of the QD as it is tuned across the MPhC nanocavity with a = 310 nm and δd = 16 nm by changing the measurement temperature. b The fitted intensity of the QDs corresponding to the spectra in (a), where ΔE is the QD-cavity mode detuning energy. c The decay curves of QDs in bulk material, non-resonance, and resonance with the cavity and the IRF of system. d The statistical analysis of the lifetimes for QDs in bulk, in resonance, and non-resonance with MPhC nanocavities. The black line is the average lifetime of QDs in bulk. e Second-order correlation measurement of single photons emitted by the QD in bulk (left) and the QD coupled with MPhC nanocavities (right).

To further confirm the Purcell enhancement factor, we implemented time-resolved PL spectroscopy for QDs in different conditions. Figure 5c shows the raw fluorescence decay data for QDs under different conditions. The black dots show the typical decay curve of a QD in bulk material (τ_Bulk = 906 ± 150 ps). The red dots correspond to the decay curve of the QD that is nonresonant with the MPhC cavity mode (τ_Non = 2500 ± 9 ps). The blue dots correspond to the decay curve of QD in resonance with the cavity (τ_In = 282 ± 7.7 ps). To confirm that the observed variation in the QD spontaneous emission rate is primarily due to the coupling with the nanocavity as the temperature changes, a control experiment is presented in Supplementary Note 11. The lifetime decay curve of the QD in resonance with the MPhC nanocavity mode exhibits the biexponential decay behavior, where the fast decay component of the decay curves is caused by the Purcell enhancement⁶⁰ and the slow decay component might be due to QD refilling by carriers captured from charge centers and surrounding excitonic bath⁶¹. The decay rate of the QD in resonance with the cavity exhibits an enhancement with a factor of three compared to the QD in the bulk material, which is limited by the instrument response function (IRF) of the system (τ_IRF = 288 ± 8.0 ps, gray dots). Since the lifetime of the QD in resonance with the cavity modes is close to the IRF of the system, it is difficult to obtain convincing results by deconvolution. To show the potential of our system for future applications⁶², we calculate the theoretical Purcell factor using both experimental Q and theoretical Q. When the dipole is located >50 nm from the edge of the center hole, the calculated Purcell factor ranges from 50 to 233 when using the experimental Q. More details are shown in Supplementary Note 10.

To further explore the CQED effect, we have conducted a statistical analysis of the lifetimes of multiple QDs in different conditions, as shown in Fig. 5d.The black line denotes the fitted average lifetime value (~906 ps) of the QD lifetimes in the bulk material (~140 QDs). The red dots represent the lifetime statistics for QDs embedded in the MPhC superlattice structures, which are not resonant with the cavity mode. In this case, the spontaneous emission from the QDs is suppressed due to the presence of the photonic bandgap of the MPhC superlattice structures, resulting in a longer lifetime compared to the QDs in bulk material. The blue dots represent the lifetime statistics of QDs in resonance with the cavity mode. We observed that the spontaneous emission rates are either suppressed or enhanced for QDs, depending on their interaction with the bandgap or the cavity mode, respectively. Some of the lifetime measurement results are presented in Supplementary Note 12, including those for Purcell-enhanced QDs (Supplementary Fig. 13) and radiation-suppressed QDs (Supplementary Fig. 14). The observed Purcell effect in experiments is further discussed in Supplementary Note 13. We have evaluated the quantum efficiency by assuming the value of the nonradiative decay rate from 0.01 μeV to 0.1 μeV⁶³. The corresponding efficiency without (with) Purcell effect ranges from 0.9397 (0.9930) to 0.9939 (0.9993) in Supplementary Note 14. This result suggests the Purcell factor is high enough for a range of applications, such as single-photon sources and low-threshold lasers.

Finally, we performed second-order correlation (g2) measurement to demonstrate the enhanced single-photon emission by coupling the QD with the MPhC nanocavity. Left panel in Fig. 5e is the g² of the bulk QD, exhibiting a g²(0) of 0.65 before deconvolution. In contrast, right in Fig. 5e shows the g² of the QD resonant to the cavity mode. The linewidth of the fitted curve is narrower than that of the QD in bulk, where the linewidth reflects the lifetime of exciton emission. The value of g²(0) = 0.28 ± 0.10 is obtained, which confirms the single-photon emission from the QD and the improvement of single-photon emission by the MPhC nanocavity. We emphasize that the time-resolved spectroscopy in Fig. 5 is limited by the convolution of IRF. The actual Purcell factor could be higher, and the actual g²(0) should be smaller than the values extracted from the raw spectra. Nonetheless, the comparison between the QDs in different conditions clearly demonstrates the Purcell effect from the cavity-QD coupling.

Sample fabrication

The QD samples used to fabricate the suspended moiré superlattice structures were prepared via molecular beam epitaxy. A layer of self-assembled QDs is embedded within 150 nm-thick GaAs slabs grown on a 1 μm-thick AlGaAs sacrificial layer. The moiré superlattice pattern is defined in the resist using high-resolution electron beam lithography. The pattern is then transferred into the GaAs layer through inductively coupled plasma etching. The remaining resist is removed by immersing the sample in dimethylformamide. Finally, the AlGaAs sacrificial layer is selectively etched away using diluted hydrofluoric acid, resulting in a suspended GaAs photonic crystal slab with the moiré superlattice pattern.

Experimental setup

Moiré superlattice samples were mounted in a closed-cycle cryostat with a temperature of 4.2 K. In optical measurement, a confocal microscopy system was used with a ×100, numerical aperture = 0.70 objective for both excitation and PL collection. Excitation sources, including a continuous-wave 532 nm semiconductor laser and an ultrafast pulsed laser, were used for different measurements. The emitted photons were directed into a spectrometer fitted with a 1200 g/mm grating, providing a spectral resolution of 60 μeV. For time-resolved PL and second-order correlation analyses, the monochromator and an adjustable slit were used as a tunable bandpass filter. Filtered photons were detected by single-photon avalanche diodes, and lifetime and photon statistics were recorded by using a time-correlated single-photon counting technique.

Numerical simulations

The theoretical results were calculated using 3D finite-difference time-domain methods. The geometric parameters defining the moiré superlattice were extracted directly from SEM images. The band structure diagram of the moiré superlattice, as well as the spectra and field distributions of the moiré cavity, were all obtained by exciting the structure with dipole sources. For cavity mode, in-plane electric field distributions were obtained in the mid-plane along the z axis of the slab.

References

Authors and Affiliations

1. Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing, China

   Sai Yan, Rui Zhu, Shushu Shi, Yu Yuan, Danjie Dai, Zhanchun Zuo, Can Wang & Kuijuan Jin

2. School of Physical Sciences, University of Chinese Academy of Sciences, Beijing, China

   Sai Yan, Rui Zhu, Shushu Shi, Yu Yuan, Danjie Dai, Zhanchun Zuo, Can Wang & Kuijuan Jin

3. State Key Laboratory for Mesoscopic Physics and Frontiers Science Center for Nano-optoelectronics, School of Physics, Peking University, Beijing, China

   Hancong Li, Jingnan Yang, Xiqing Chen, Zhikai Ma, Longlong Yang, Wenshuo Dai, Bowen Fu, Qihuang Gong & Xiulai Xu

4. State Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors, Chinese Academy of Sciences, Beijing, China

   Hanqing Liu, Deyan Dai, Haiqiao Ni & Zhichuan Niu

5. Songshan Lake Materials Laboratory, Dongguan, Guangdong, China

   Can Wang & Kuijuan Jin

6. Peking University Yangtze Delta Institute of Optoelectronics, Nantong, Jiangsu, China

   Xiulai Xu

7. Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, Shanxi, China

   Xiulai Xu

Contributions

X.X., C.W., K.J., and Q.G. supervised the research project. S.Y. fabricated the Moiré superlattice structures. Z.N., H.N., H.L. (Hanqing Liu), and D.D. (Deyan Dai) contributed quantum dot samples. S.Y., H.L. (Hancong Li), J.Y., X.C., R.Z., Z.M., S.S., L.Y., Y.Y., W.D., D.D. (Danjie Dai), B.F. and Z.Z. performed the optical measurements. S.Y. performed the simulations. S.Y., H.L. (Hancong Li), J.Y., and X.X. analyzed the data and wrote the manuscript with substantial contributions from all the others.

Corresponding authors

Correspondence to Can Wang or Xiulai Xu.

Competing interests

The authors declare no competing interests.

Peer review information

Nature Communications thanks Alexey Lyasota and Ren-Min Ma for their contribution to the peer review of this work. A peer review file is available.

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions