In this Rust Bits post, we dive into Rust’s comparison traits and how equality and ordering work across built-in and user-defined types.
Equality and ordering are foundational to collections, sorting, and algorithms.
Rust encodes these semantics explicitly with PartialEq/Eq and PartialOrd/Ord, balancing mathematical rigor with practical ergonomics.
Rust models equality and ordering via four core traits: PartialEq / Eq and PartialOrd / Ord.
Understanding what each guarantees, how they relate hierarchically, and the Ordering values they produce is essential since everything else (operators, sorting, and collections) builds on these definitions.
The Ordering enum represents the result of a comparison:
The relationship between the traits is hierarchical:
Ord implies Eq and provides a blanket PartialOrd (every Ord is also a PartialOrd).
Eq implies PartialEq.
PartialEq / PartialOrd allow “incomparable” cases (e.g., floats with NaN).
Rust distinguishes total and partial comparisons to encode mathematical laws in the type system without sacrificing practicality.
Integers admit a total order and strict equivalence, whereas IEEE-754 floats do not due to NaN semantics.
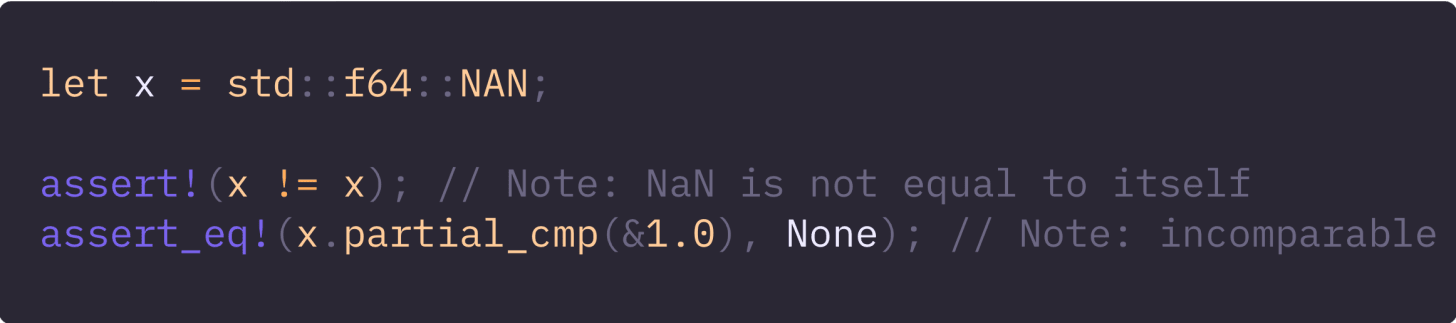
Floats demonstrate partial comparisons: NaN is not equal to itself and not comparable.
Sorting floats needs an explicit total ordering, while integers can use Ord directly.
These traits come with algebraic laws that Rust expects implementations to uphold, ensuring predictable behavior in operators, sorting, and collections.
The following properties highlight what Eq and Ord require, what PartialEq / PartialOrd relax, and why floats illustrate these constraints:
Eq must be an equivalence relation: reflexive (x == x), symmetric, transitive.
Ord must be a total order: for any x & y, exactly one of x < y, x == y, x > y must hold; and transitivity must hold.
PartialEq / PartialOrd allow None / incomparability while still giving you == / != and relational operators where defined.
This rigor is why f64 cannot implement Eq or Ord: NaN violates reflexivity and totality.
This is also why deriving PartialEq, Eq, PartialOrd, and Ord is so useful: the generated implementations obey the laws for common cases.
Beyond the theory, comparisons show up constantly in everyday Rust through operators, explicit comparators, and trait bounds on collections.
This section surveys the idiomatic patterns you’ll use most: == / != and < comparisons, cmp / partial_cmp, and where Eq / Ord drive sets, maps, and sorting APIs.
Direct comparison operators using PartialEq and PartialOrd for equality checks and ordering:
Explicit comparison methods for custom sorting and comparison logic:
Collection keys and sorting algorithms that require specific comparison traits:
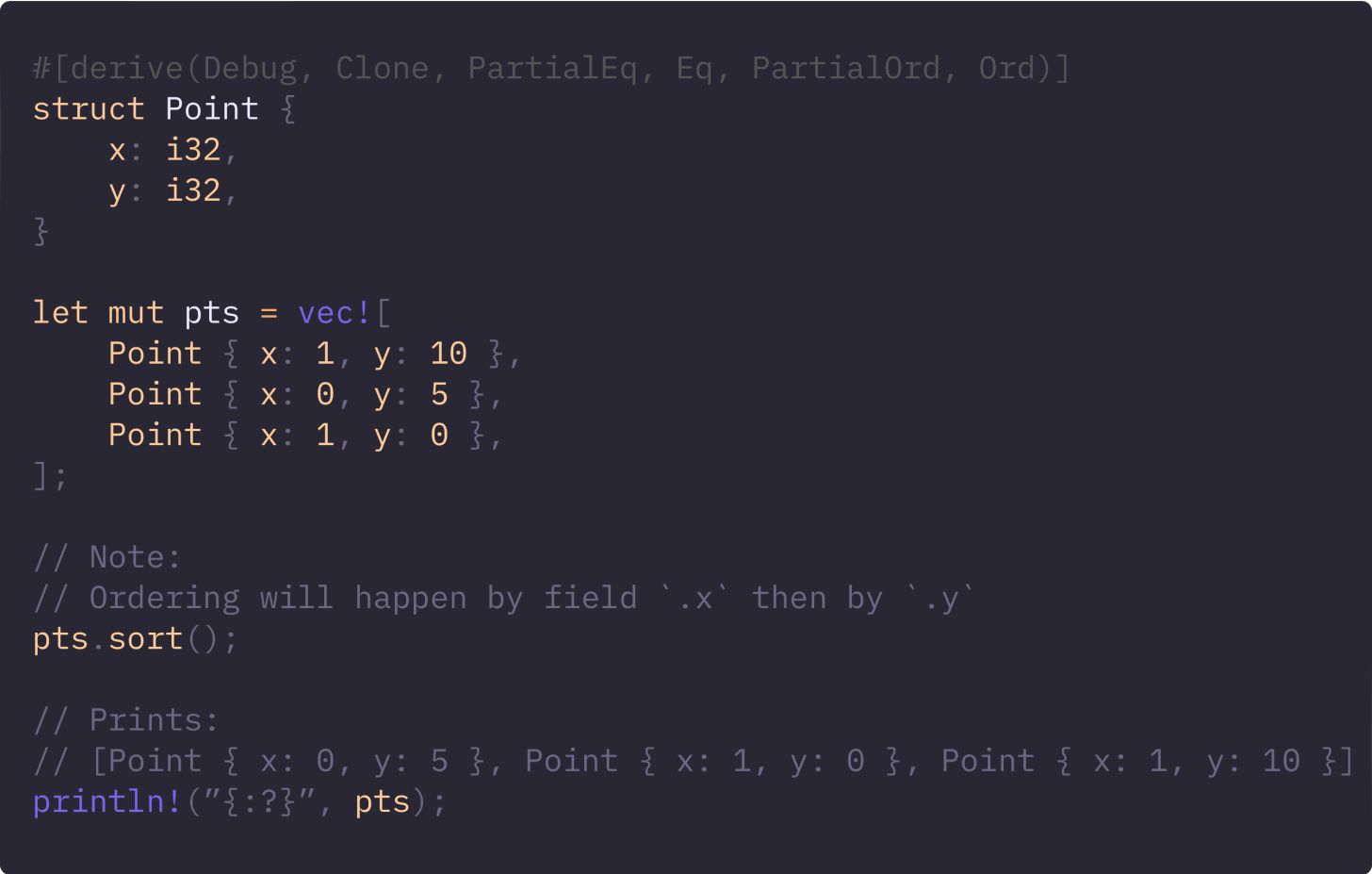
For data types composed of comparable fields, deriving PartialEq / Eq / PartialOrd / Ord is the fastest way to get correct, law-abiding implementations.
Derives produce lexicographic ordering for structs and declaration order for enums, which affects both semantics and performance.
Derived ordering is lexicographic by field order. For enums, variant order is declaration order.
Real-world sorting often means ordering by derived keys, flipping directions, and composing tie-breakers.
This section demonstrates the standard combinators for building clear, deterministic comparators from simple pieces.
Order collection via custom value with sort_by_key()
Reverse an order with std::cmp::Reverse.
Chain comparisons with Ordering::then / Ordering::then_with.
Floats highlight why Rust splits partial versus total comparisons: This distinction ensures safe and predictable behavior when dealing with floating-point numbers, which can represent NaN values that complicate equality checks.
Equality: Eq must be reflexive — f64 can’t satisfy that because NaN != NaN.
Ordering: Ord must be total; NaN breaks totality, thus we need to use total_cmp for deterministic sorting.
Sometimes, incomparability is the correct model: In Rust’s type system, this concept shines through traits like PartialOrd, where values can remain incomparable to accurately represent scenarios lacking a total order.
Intervals can be incomparable when they overlap.
Many core collections and algorithms express their requirements via trait bounds such as Eq, Ord, and Hash.
Understanding which traits your types implement determines where they can be used (e.g., as keys) and which sorting APIs are available.
BTreeMap / BTreeSet require Ord to maintain sorted keys, while HashMap / HashSet require Eq + Hash.
Sorting APIs leverage Ord by default, or accept comparators for custom logic.
Rust’s comparison calls inline efficiently; the primary cost comes from data you compare:
Prefer comparing small, fixed-size keys (e.g., integers) before expensive ones (e.g., large strings).
For derived Ord, field order affects performance and semantics — put the cheapest & more-selective fields first.
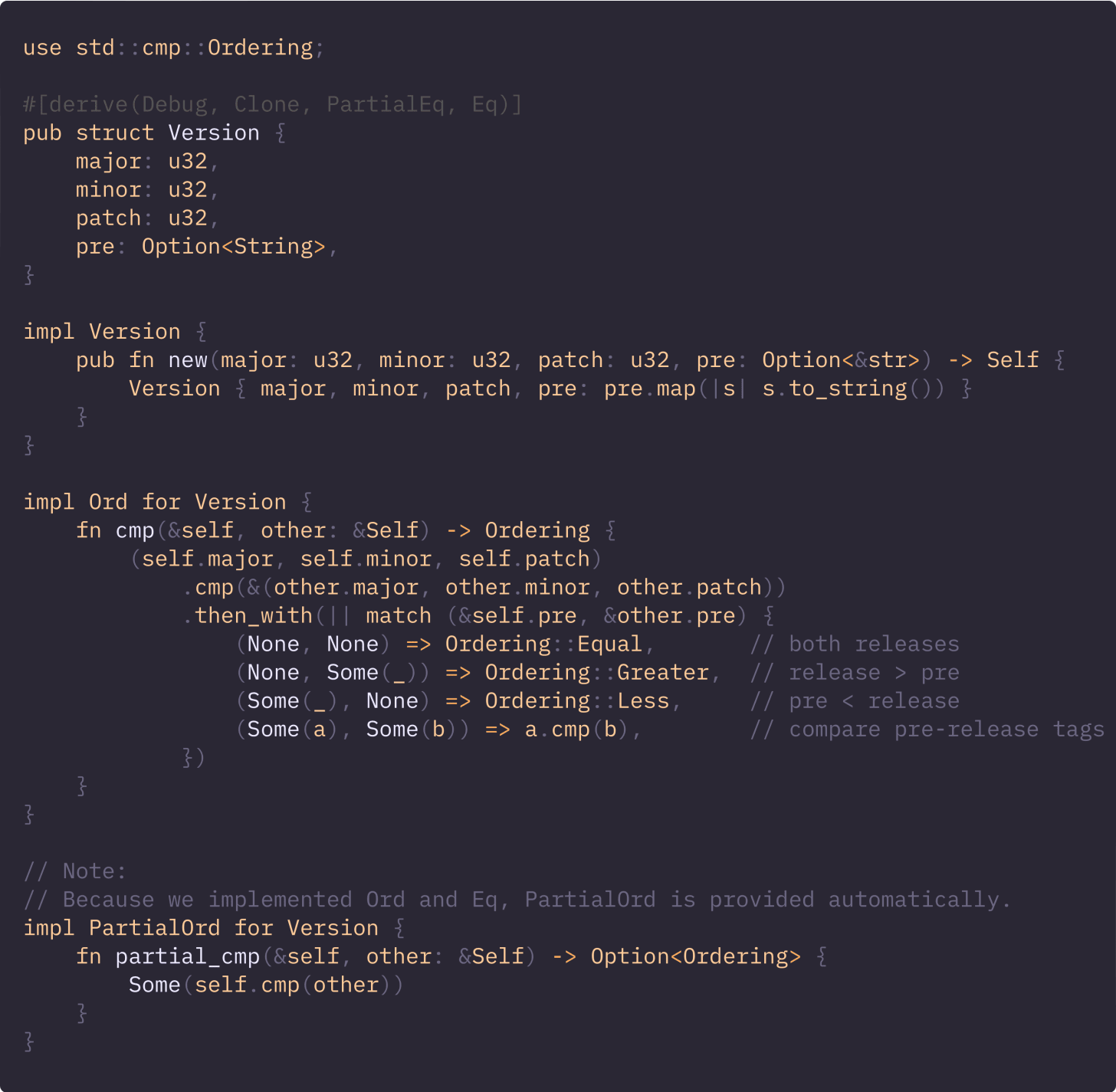
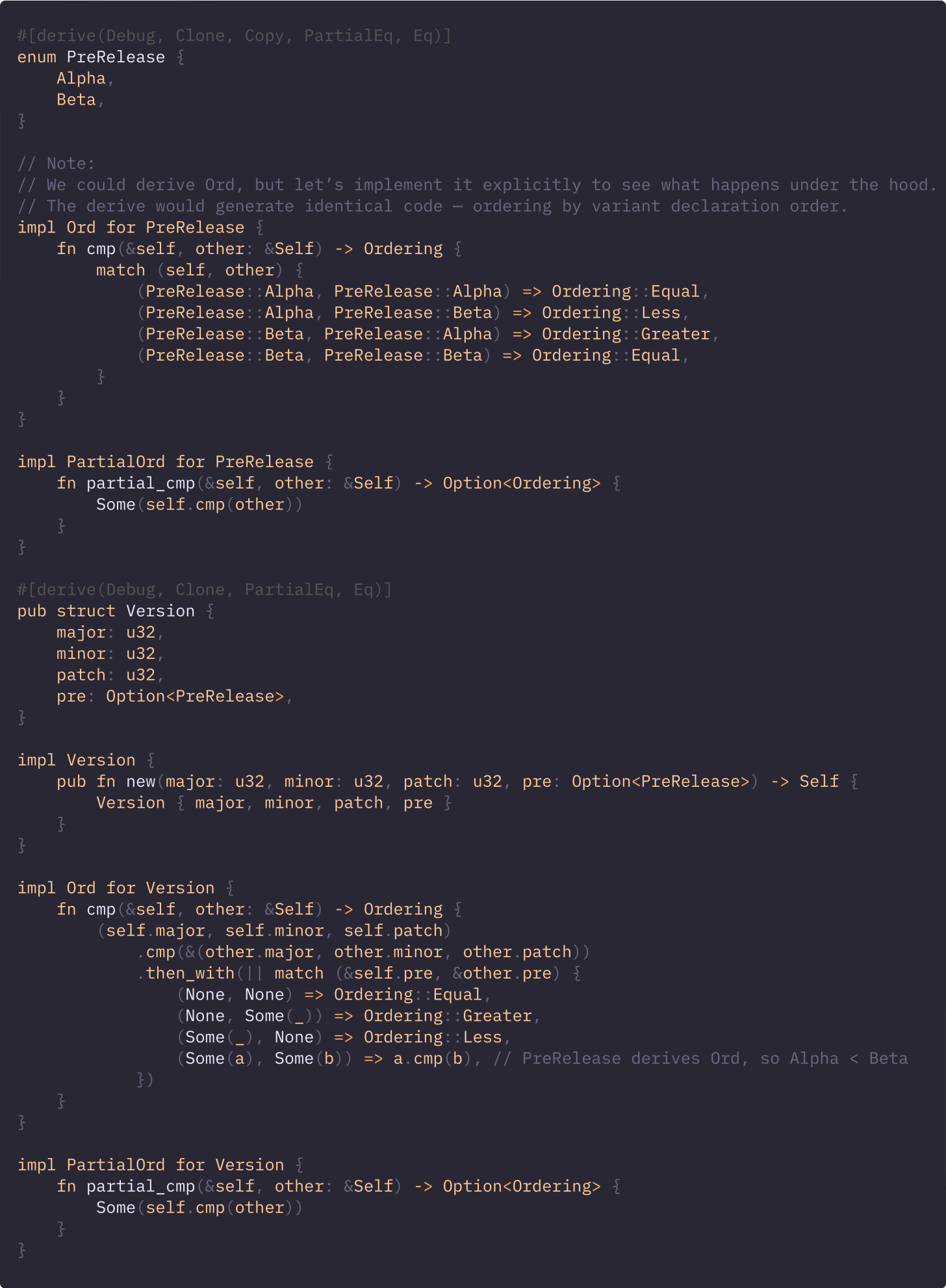
As a closing note, let’s go through a slightly more complex example of a Version (1.0.1-alpha) type with optional pre-release identifiers:
major, then minor, then patch
Release > any Pre-Release
For two Pre-Releases, compare their strings lexicographically
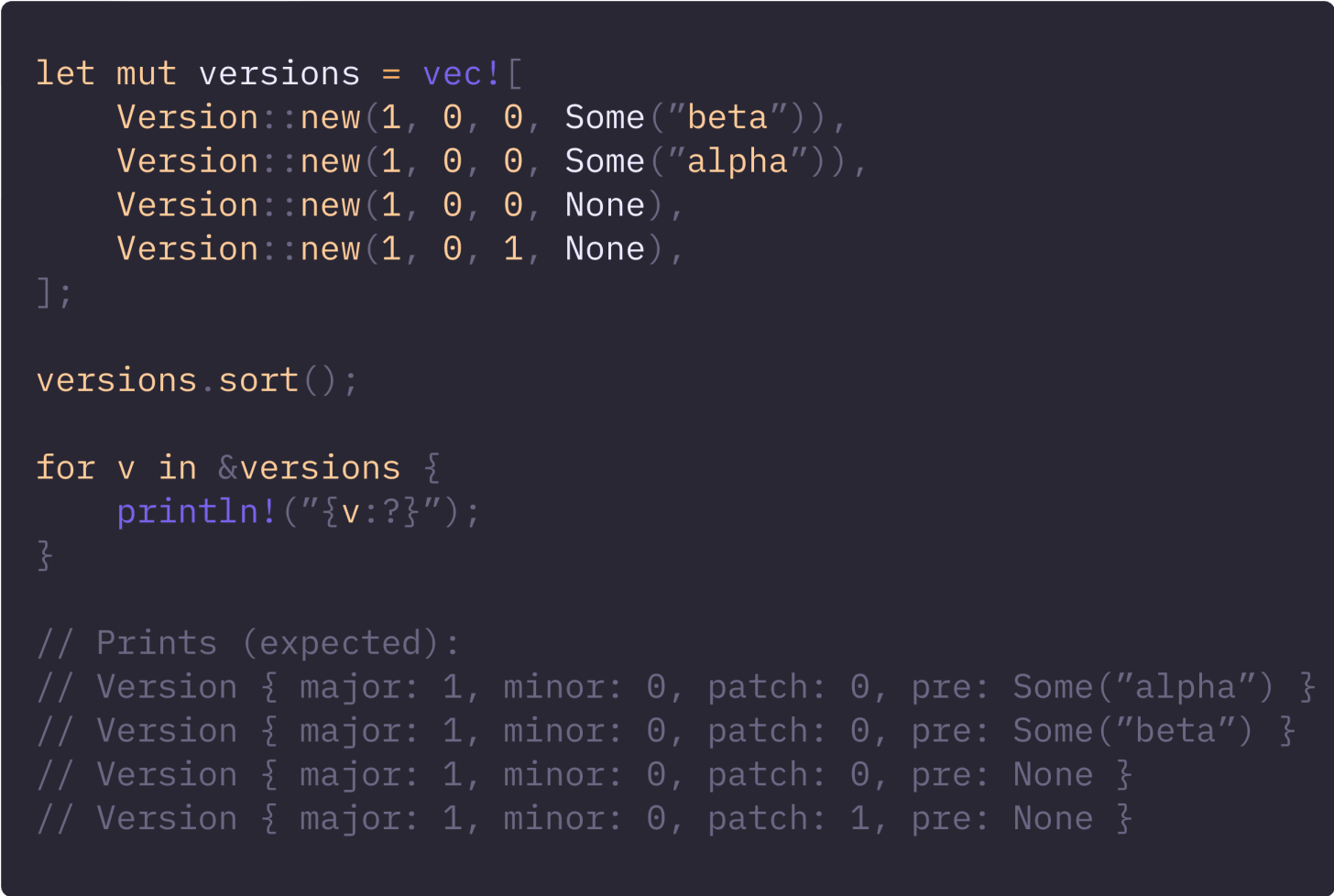
Given the requirements, we can write a test that validates the functionality:
A naive derive would order Option as None < Some by default, which is opposite to our semantics (release > pre-release), so we implement Ord manually.
Great, now let’s use it:
Let’s improve our Version type by replacing the String-based pre-release identifiers with a proper enum. This gives us type safety and explicit ordering.
Testing the improved version:
With this, we implemented a custom, law-abiding total ordering that differs from the default derive and matches domain rules precisely.
Rust splits equality and ordering into partial (PartialEq / PartialOrd) and total (Eq / Ord) variants to model real-world data correctly.
Ord implies Eq and provides a total order — it’s required by sorted collections like BTreeMap / BTreeSet and by sort() itself.
Floats only implement PartialEq / PartialOrd due to NaN. Use total_cmp for sorting, and avoid using floats as keys in structures requiring Eq / Ord / Hash.
Deriving comparisons is the simplest path — field order defines lexicographic priority and performance.
Implement traits manually when domain semantics differ from the default (e.g., Release > Pre-Release).
Prefer cheap & selective keys first, along with sort_by_key, Reverse, and Ordering::then_with for clear, composable comparators.
Understanding when to use partial vs total comparisons — and how to implement both correctly — is crucial for writing robust, idiomatic Rust that behaves predictably across collections and algorithms.
.png)