Convergence vs. Consensus in Distributed Systems

Convergence and consensus are two closely-related properties of distributed systems implementing the replicated state machine (RSM) abstraction. While convergence requires replicas to eventually agree on the value of a decision variable, consensus requires them to never disagree. This subtle distinction makes all the difference in practice: while convergence can be implemented using relatively simple abstractions that guarantee high availability, such as CRDTs (and our own homegrown MRDTs), consensus requires sophisticated coordination protocols that induce unavailability, such as Paxos and Raft. But what exactly is the relationship between convergence and consensus? And how do replicated data types (RDTs) relate to Paxos and Raft? In our recent OOPSLA paper, we formally answered these questions and leveraged the insights to develop a simpler formal verification technique for consensus protocols. In this blog post, I explain our observations regarding convergence-consensus relationship. If time permits, I will follow this up with another post explaining the implications to formal verification.

Eventual Agreement vs Lack of Disagreement

Consider a replicated database that supports distributed transactions. Let’s say a banking application is using the database to store and replicate bank account information and facilitate financial transactions, such as withdraws and transfers. Assume the replication factor is 3, i.e., there are three copies of each bank account. Users submit transactions, which may execute successfully and commit their results or may fail and abort; in either case, the status (commit or abort) is communicated to the user. To maintain a consistent bank account information, all replicas have to agree on the status of a transaction, otherwise some replicas might commit and others abort resulting in divergence of state. For illustration, consider a simple withdraw transaction on a bank account object:

For brevity, we will write withdraw(a) as W(a), e.g., withdraw(100) as W(100). Consider the following execution on a replicated bank account object with the initial balance as $200. A transaction W(150) submitted by a user is executed and committed on replica \(R_3\) and also broadcast to other replicas. Before W(150) reaches \(R_1\), another transaction W(100) is executed and committed. Subsequently, W(150) fails on \(R_1\) due to the lack of sufficient balance and is aborted. By the time indicated by the dotted line, we have replicas disagreeing on the status of the transaction W(150) and, consequently, ending up with diverging balances. Granted, W(100) is yet to be applied on \(R_2\) and \(R_3\), but doesn’t change anything as the transaction simply fails at both places.

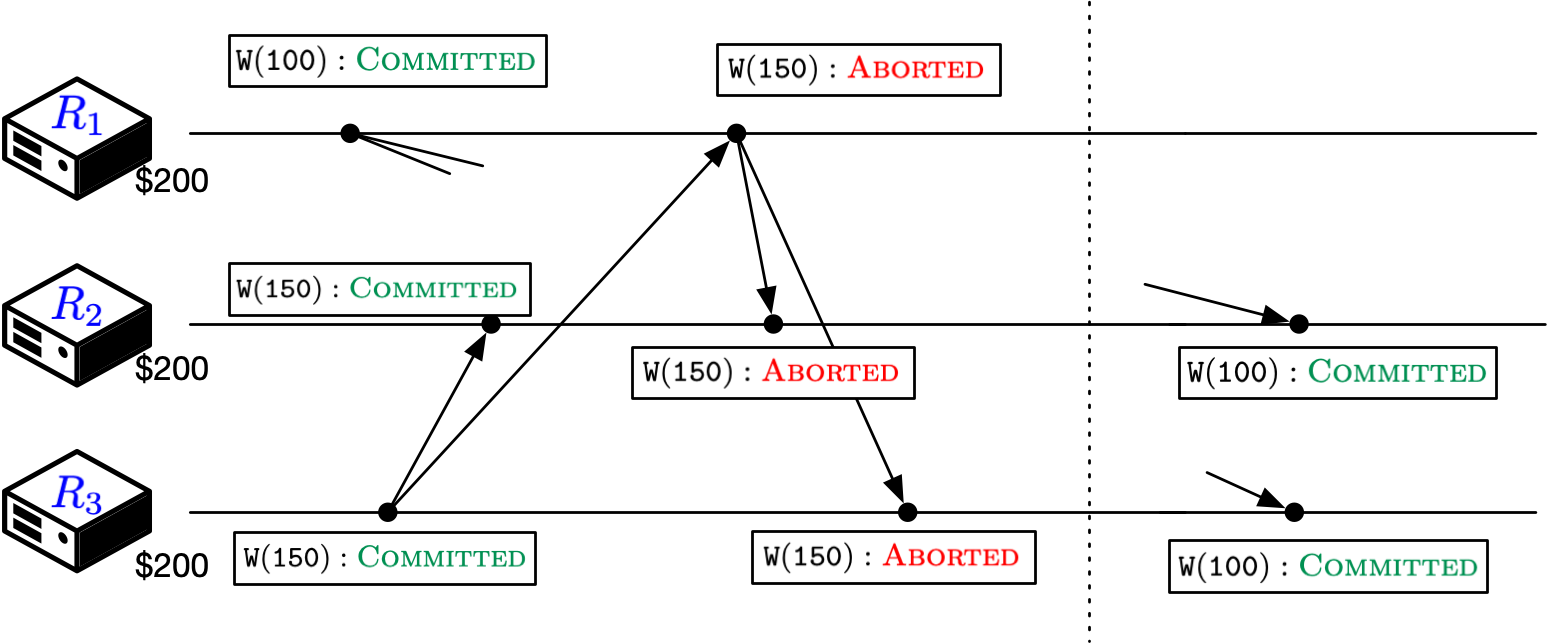
It is possible to “fix” this divergence by shepherding the replicas towards an eventual agreement on the status of W(150). In the spirit of CRDTs, we can resolve the conflict between the two concurrent operations—W(150) and W(100)—by letting the latter “win” (based on their unix timestamps, for example). This results in the execution shown to the right of the dotted line: on delivery of W(100), \(R_2\) and \(R_3\) “reset” the status of W(150), undo its effects, and execute+commit the newly delivered transaction. The end result is a convergent execution where replicas eventually agree on the status of W(150) as Aborted although they transiently disagree. All seems well.

But not quite: when W(150) was originally marked Committed on \(R_3\), the funds could have been transferred out the banking system, which now need to be recovered through some extraneous process, perhaps by mailing the user and requesting them to return the funds. Thus, even if the replicas eventually reach an agreement, it is possible that they make incorrect decisions during the transient disagreement phase that may not be reversible. Avoiding such situations requires us to go beyond eventual agreement and guarantee there is never a disagreement in the first place. In the current example, this means that replicas should never disagree on the status of the W(150) transaction, i.e., the prefix of the execution to the left of the dotted line shown above should be impossible. Enforcing this requires a coordination protocol to orchestrate consensus across replicas, which is what protocols such as Two-Phase Commit, Paxos, and Raft do.

What exactly is lack of disagreement?

Let us take a closer look at what a lack of disagreement means in the context of the current example. Intuition suggests that the status of a transaction should be the same across all replicas, but this is not quite right as replicas do not work in lock step. The following example demonstrates. Shown below is an execution of a quorum-based commit protocol with simple majority quorums, i.e., a majority of replicas must commit a transaction for it to be considered committed.

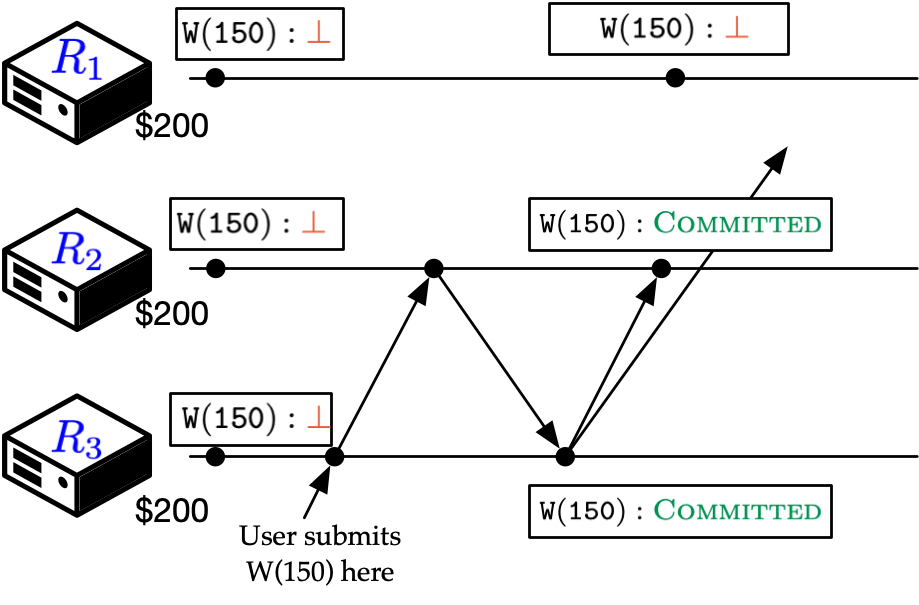
Here, transaction W(150) was submitted at \(R_3\), which executes and broadcasts it to all replicas. Replicas \(R_3\) and \(R_2\) vote to commit it, resulting in a quorum. Consequently, \(R_3\) commits and brodcasts the commit status, which \(R_1\) receives and updates its local state. Throughout this process, a network partition prevents \(R_1\) from receiving any updates, making it unaware of W(150). The status of W(150) on \(R_1\) therefore reads ⊥ (bottom or unknown), making it different from the status on \(R_2\) and \(R_3\). Does it mean \(R_1\) disagrees with \(R_2\) and \(R_3\)? No; it has simply fallen behind its peers and will catchup when the network partition heals. This tells us that the decision value being unequal does not necessarily mean that there is a disagreement. We therefore define a new relation to characterize disagreement—the conflict relation (\(\bowtie\)). Let \(S_1(T)\) and \(S_2(T)\) be two possible statuses for transaction \(T\). We define:

\[\begin{array}{lcl} S_1(T) \bowtie S_2(T) & \Leftrightarrow & (S_1 = Committed \wedge S_2 = Aborted) \vee (S_1 = Aborted \wedge S_2 = Committed)\\ \end{array}\]

In other words, \({Committed}(T)\) status conflicts with \({Aborted}(T)\) status, but neither conflict with \(\bot(T)\). Using this relation, we can now define disagreement: a pair of replicas, \(R_1\) and \(R_2\) disagree with each other if their respective decisions, \(D_1\) and \(D_2\), conflict, i.e., \(D_1 \bowtie D_2\). The choice of the conflict relation can depend on the domain; see Sec. 3.1 of our paper for examples.

Temporal Aspect of Disagreement

There was some sleight of hand involved in the above definition of disagreement: by considering two distinct replicas, \(R_1\) and \(R_2\), we made it an implicitly spatial relationship. What if we have only one replica? Can it disagree with itself? Well, not across space, but it can across time! For example, it can flip its decision on the status of a transaction \(T\) from \(Committed(T)\) to \(Aborted(T)\), thus invalidating all prior downstream effects. A practical transaction processing system might want to preempt such temporal disagreements as well. Fortunately, this is straightforward: we simply require the consecutive states of a replica to never be in conflict, i.e., we prohibit state transitions that contradict the current decision. In the transaction processing example, the legal state transitions can be visualized as the following partial order of possible decisions:

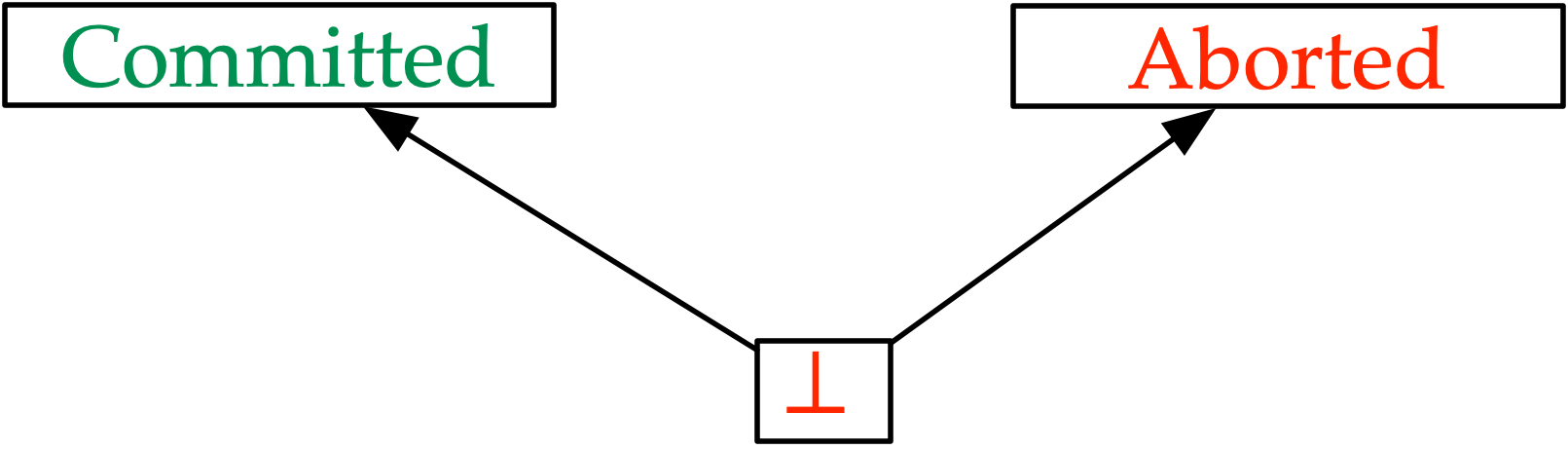
Given a transaction \(T\), it’s ok to transition from \(T:\bot\) to \(T:Committed\) or from \(T:\bot\) to \(T:Aborted\), but the transitions \(T:Committed \rightleftarrows T:Aborted\) are disallowed. If we view the above diagram as a semi-lattice, then only legal transitions are those that move “up” the lattice. We call this property monotonicity. From the above discussion, it is clear that monotonicity is a necessary property to ensure lack of disagreement (i.e., consensus): A replica is never allowed to “flip” its decision in a way that contradicts its previous decision. But is monotonicty a sufficient condition for consensus?

The Punchline

Assuming the system otherwise guarantees convergence, monotonicity is indeed a sufficient condition for consensus. That is:

\[\begin{array}{c} Convergence ~+~ Monotonicity ~=~ Consensus \end{array}\]

To understand the intuition, let’s reconsider the our transaction processing system. Given a transaction \(T\), the decision space is the finite semi-lattice shown above. All replicas start at the bottom of the lattice, i.e., \(T:\bot\). A replica can progress either by silent/stutter transitions that do not change its current decision or by one of the two legal transitions: \(T:\bot \rightarrow T:Committed\) or \(T:\bot \rightarrow T:Aborted\). If some replicas take the first transition and the other take the second, then we end up with divergence since \(T:Committed\) and \(T:Aborted\) cannot be reconciled as per our lattice. However, this case is impossible as it violates our assumption that the system guarantees convergence. Therefore, it should be the case that all replicas take the same transition and end up with either \(T:Committed\) or \(T:Aborted\). In other words, as long as we ensure that (a). replicas are locally monotonic, and (b). system as a whole converges, then we are guaranteed to never have disagreement! This is cool because we can (formally) verify convergence and monotonicity separately to (formally) verify consensus. How do we verify convergence? Thanks to CRDTs, there’s a ton of work on that. And how do we verify monotonicity? Well, monotonicity is a local property—it is only concerned with local transitions of a replica—so can be verified just like any other sequential program property. Our paper develops a proof technique based on this observation and demonstrates how it can be used to formally verify an implementation of the Raft protocol using only SMT solvers (i.e., without any manual proof). I will explain more about our proof technique and formal verification efforts in the next blog post. The key takeaways for now should be that (a). convergence (eventual agremeent) is strictly weaker than consensus (lack of disagreement), and (b). monotonicity is the missing property that relates both.