Do Black Holes Need Singularities?

Whenever someone talks about black holes, they almost always talk about the event horizon and the singularity. After all, that's what defines a black hole, right? Well, it depends on what you mean by black hole. There are some that would argue a black hole doesn't need a singularity, and that could mean they don't even have an event horizon.

Before we dive into black holes, let's first distinguish between the two types. On the one hand, we have theoretical black holes as described in general relativity. These are solutions to Einstein's GR field equations known as metrics. The first black hole metric was discovered by Karl Schwarzschild and describes a simple, non-rotating black hole. Other metrics have been found over the years, such as the Kerr metric discovered in 1963 by Roy Kerr, which describes an uncharged rotating black hole. This is the metric used to visualize all those cool scenes in movies such as Interstellar.

*In 1979 Jean-Pierre Luminet made the first simulation of how a black hole would warp light around itself. Credit: Jean-Pierre Luminet*

On the other hand, there are the black holes we have directly observed, such as M87* and the black hole at the center of our galaxy, SagA*. The Event Horizon Telescope has gathered a great deal of data on these two black holes, and from this we know they rotate and have a near-horizon structure that—to the limits of our observation—agrees perfectly with the Kerr model. Of course none of our observations can see inside a black hole, so we don't know for sure if it has a singularity. Likewise, we can't see the event horizon itself, since any light crossing the event horizon is trapped forever. So while we have no evidence to suggest black holes don't have singularities and event horizons, alternative models that agree with current observations are also theoretically possible.

*The first direct image of the supermassive black hole in our galaxy. Credit: EHT Collaboration*

The reason this matters is that while singularities and event horizons naturally appear in the black hole metrics, they also cause all manner of problems. A simple singularity is a mathematical point of infinite density and zero volume where the laws of physics break down. It's so problematic that physicists have invoked the cosmic censorship hypothesis to claim that singularities are always shrouded by an event horizon so we don't have to worry about them. But event horizons have their own problems. Since any object crossing an event horizon can never escape the black hole, the information contained within the object is forever lost to the Universe, creating an information paradox. Round and round we go.

One way to resolve all this is to find a black hole model without a singularity and event horizon. After all, general relativity is a classical theory like Newtonian dynamics. The real universe is quantum in nature, so we really should have a quantum theory of gravity. And there's some evidence that quantum physics could solve these issues. Heisenberg's uncertainty principle states that you can't have an exact mass at an exact point, so quantum theory likely prevents singularities from forming, and Hawking radiation could allow energy and information to escape a black hole in time.

Most of the theoretical explorations of these ideas focus on the quantum side of things. For example, in loop quantum gravity, the quantum foam of spacetime could mean that black holes form a "Planck star" within the event horizon rather than a singularity. A similar model known as the fuzzball appears in string theory, where the singularity is replaced by a ball of degenerate strings. There are also alternative classical theories to general relativity that can eliminate the problems of GR.

But given that there's no observational evidence for quantum gravity, alternative relativity, or string theory, why not stick with good ol' Professor Einstein? What if we assume general relativity to be true but add the constraint that singularities are banned? Is such a black hole metric possible? Yes, and it's known as the Hayward metric.

The Hayward metric is the minimal solution to Einstein's field equations with the following constraints: static, asymptotically flat, spherically symmetric, and non-singular. In contrast, the Schwarzschild model for a black hole is the minimal solution that satisfies the first three constraints. So a Hayward black hole is basically a non-rotatating Schwarzschild black hole without a singularity. But that single difference leads to several changes.

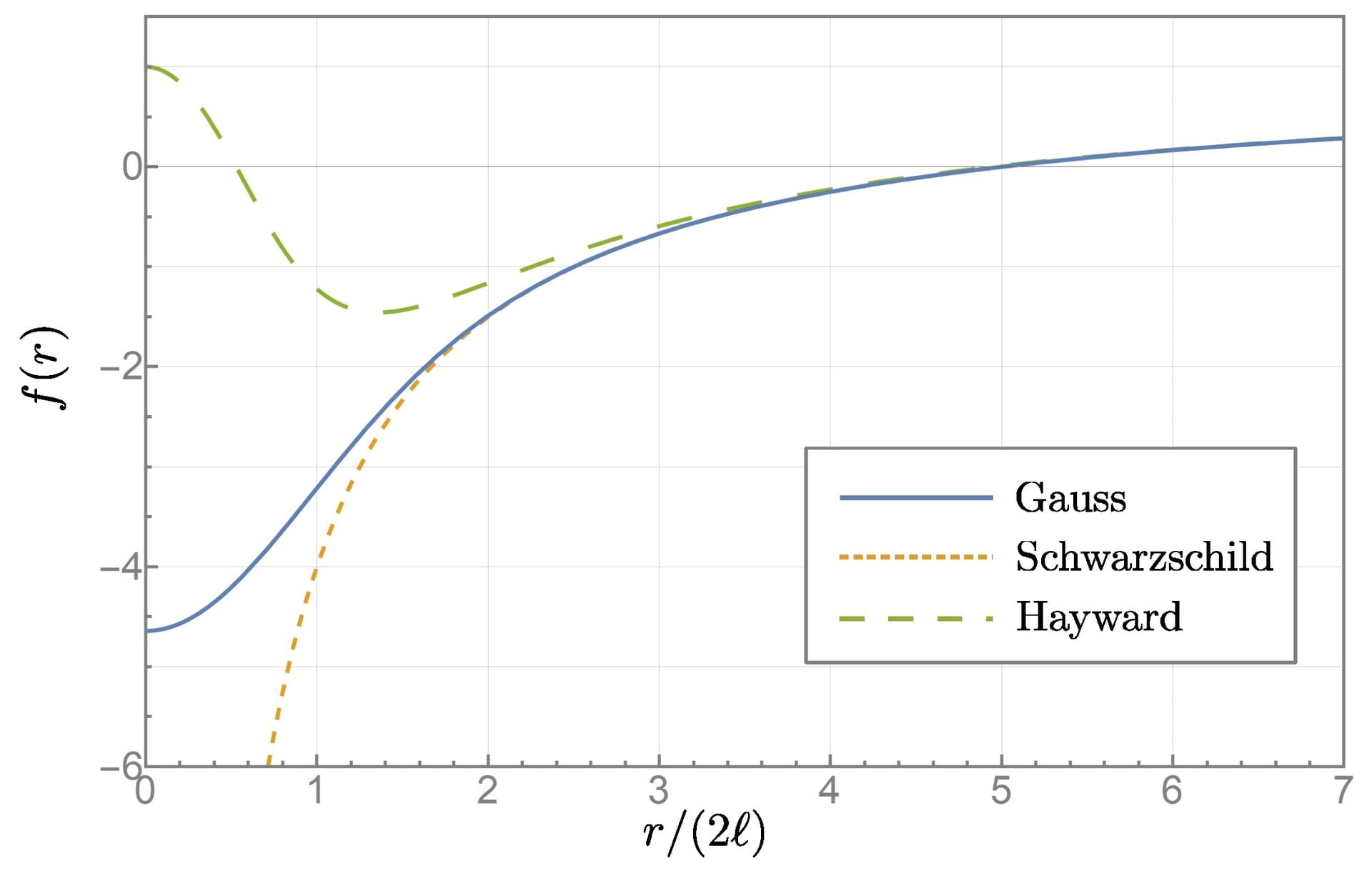*A graph comparing the Schwarzschild metric with the Hayward metric. From the outside, a Schwarzschild and Hayward black hole are nearly identical. Credit: Jens Boos/Universe*

The most obvious change is that a Hayward black hole has no singularity. Rather than space warping evermore into a vanishing point, the center of the black hole is locally flat, just like any region of deep space. A more subtle change is that Hayward black holes don't have an event horizon. Instead, the model has an apparent horizon that contains matter for a long while. Over time, matter and energy can gradually escape. It's similar to the effect of Hawking radiation but without invoking quantum physics. For supermassive black holes, this effect is so tiny that a Hayward black hole would be nearly indistinguishable from a Schwarzschild black hole. And that's the key point. Although all of our observations of black holes agree with standard models, Hayward black holes also agree with the data.

Of course, the one big catch is that we don't know of any physical mechanism that would prevent singularities from forming. The Hayward model just bans them by fiat. But if the Hayward model is correct, then all those finicky problems with singularities and event horizons could be...pointless.

Reference: Rovelli, Carlo, and Francesca Vidotto. "Planck stars." *International Journal of Modern Physics D* 23.12 (2014): 1442026.

Reference: Mathur, Samir D. "A proposal to resolve the black hole information paradox." *International Journal of Modern Physics D* 11.10 (2002): 1537-1540.

Reference: Hayward, Sean A. "Formation and evaporation of nonsingular black holes." *Physical review letters* 96.3 (2006): 031103.