Does RL Incentivize Reasoning Capacity in LLMs Beyond the Base Model?

2 hours ago 1

arXiv | project page | Authors: Yang Yue, Zhiqi Chen, Rui Lu, Andrew Zhao, Zhaokai Wang, Yang Yue, Shiji Song, Gao Huang

This paper from Tsinghua find that RL on verifiable rewards (RLVR) just increases the frequency at which capabilities are sampled, rather than giving a base model new capabilities. To do this, they compare pass@k scores between a base model and an RLed model. Recall that pass@k is the percentage of questions a model can solve at least once given k attempts at each question.

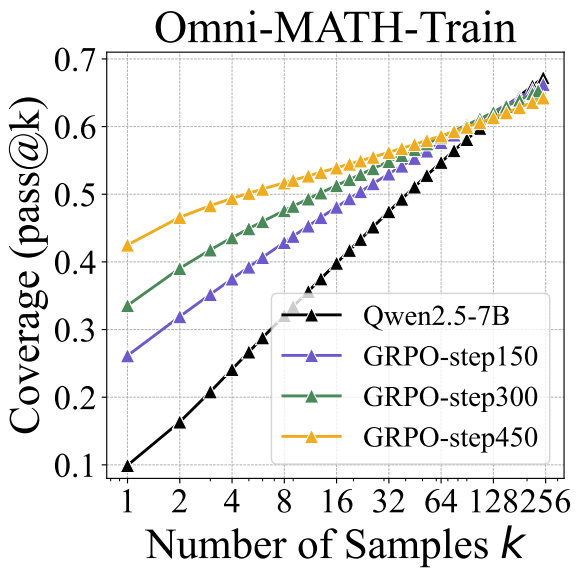
Main result: On a math benchmark, an RLed model (yellow) has much better raw score / pass@1 than the base model (black), but lower pass@256! The authors say that RL prunes away reasoning pathways from the base model, but sometimes reasoning pathways that are rarely sampled end up being useful for solving the problem. So RL “narrows the reasoning boundary”— the region of problems the model is capable of solving sometimes.

Further results

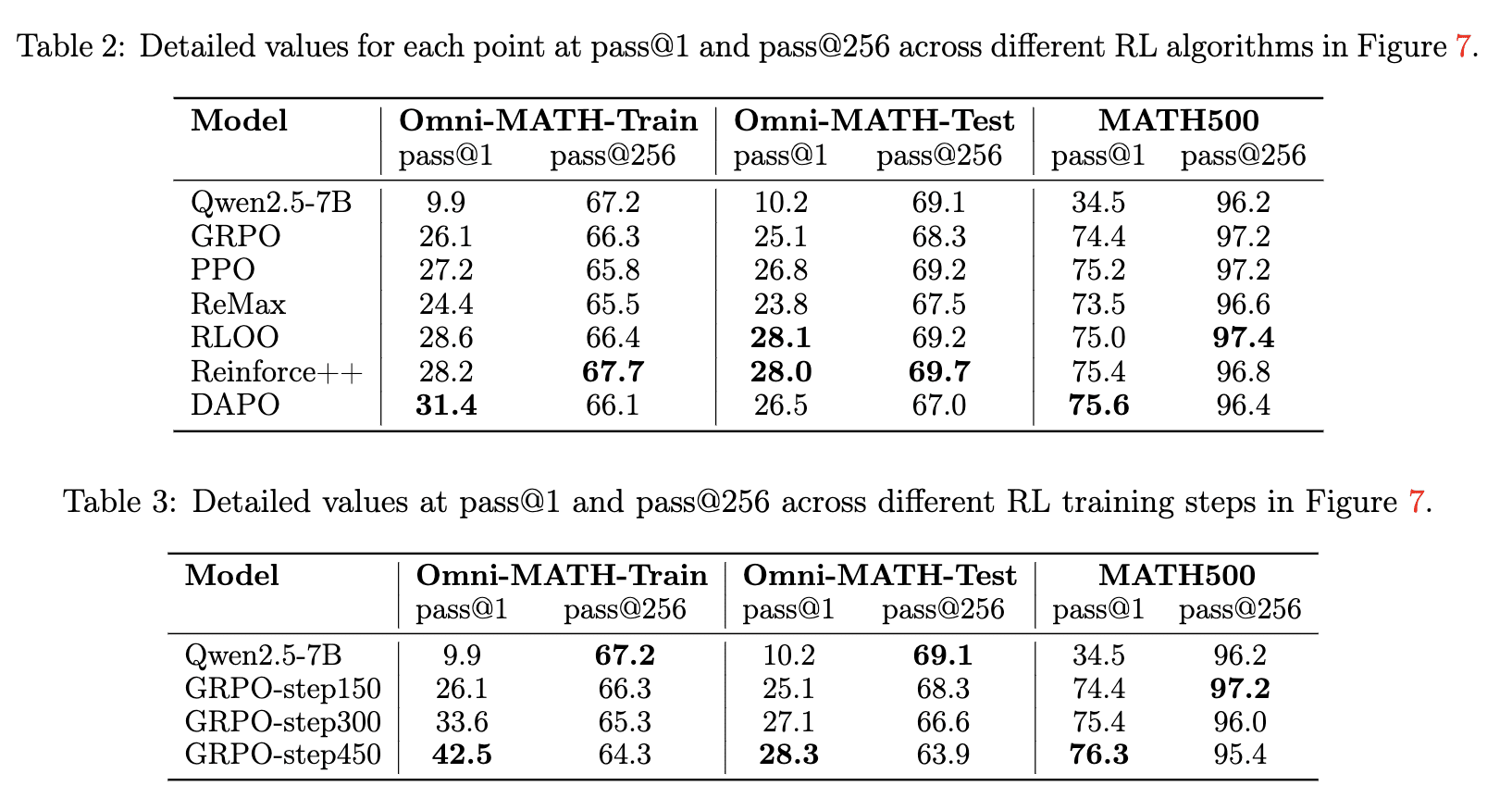
Across multiple math benchmarks, base models have higher pass@k than RLed models for sufficiently large k, and sometimes the crossover point is as low as k=4. (Figure 2)
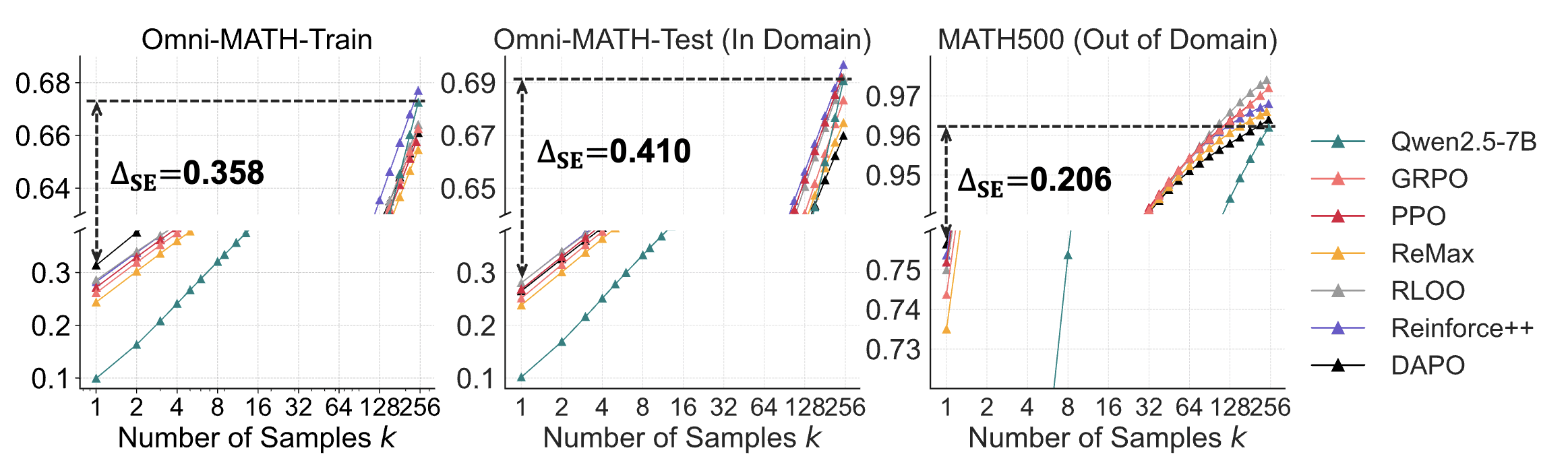
Out of domain (i.e. on a different math benchmark) the RLed model does better at pass@256, especially when using algorithms like RLOO and Reinforce++. If there is a crossover point it might be near pass@1024. (Figure 7)
To see if the pass@1024 results are just lucky guesses, they sanity check reasoning traces and find that for most questions, base models generate at least one correct reasoning trace. (But it's unclear whether the majority of correct answers are lucky guesses) Also, for long coding tasks, it's nearly impossible to make a lucky guess.
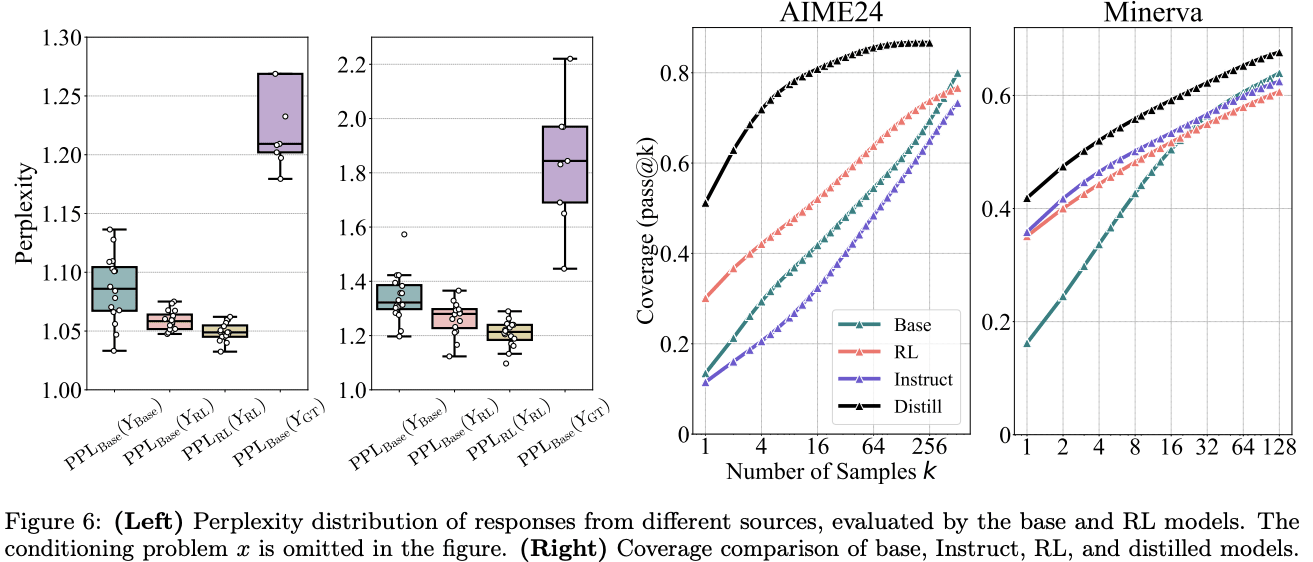
They test the perplexity (Below: Figure 6 left) of the RLed model’s generations (pink bar) relative to the base model. They find it is lower than the base model's perplexity (turquoise bar), which “suggests that the responses from RL-trained models are highly likely to be generated by the base model” conditioned on the task prompt. (Perplexity higher than the base model would imply the RLed model had either new capabilities or higher diversity than the base model.)

Distillation from a stronger teacher model, unlike RL, “expands the reasoning boundary”, so performance improves at all best@k values. (Below: Figure 6 right)

Limitations

RL can enable emergent capabilities, especially on long-horizon tasks: Suppose that a capability requires 20 correct steps in a row, and the base model has an independent 50% success rate. Then the base model will have a 0.0001% success rate at the overall task and it would be completely impractical to sample 1 million times, but the RLed model may be capable of doing the task reliably.
Domains: They only test on math, code generation, and mathematical visual reasoning, and their results on code generation and visual reasoning could be underelicited. It’s plausible that results would be different in domains requiring more creativity.
Model size: The largest model they test is 32B; it's possible RL has different effects on larger models

Takeaways

This is reminiscent of past work on mode collapse of RLHF.
Their methods seem reasonable so I mostly believe this paper modulo the limitations above. The main reason I would disbelieve it is if models frequently have lucky guesses despite their checks-- see point 3 of "further results".
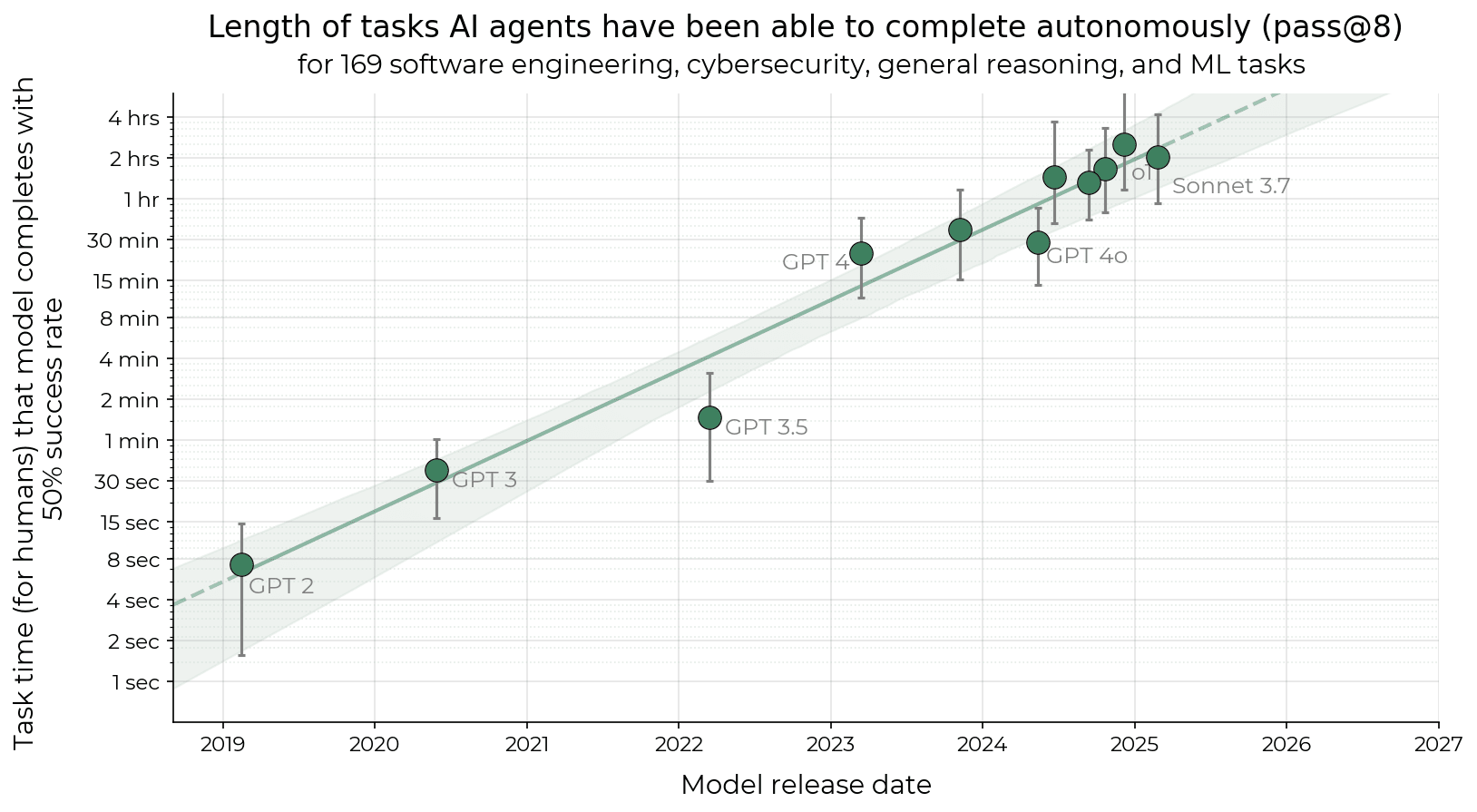
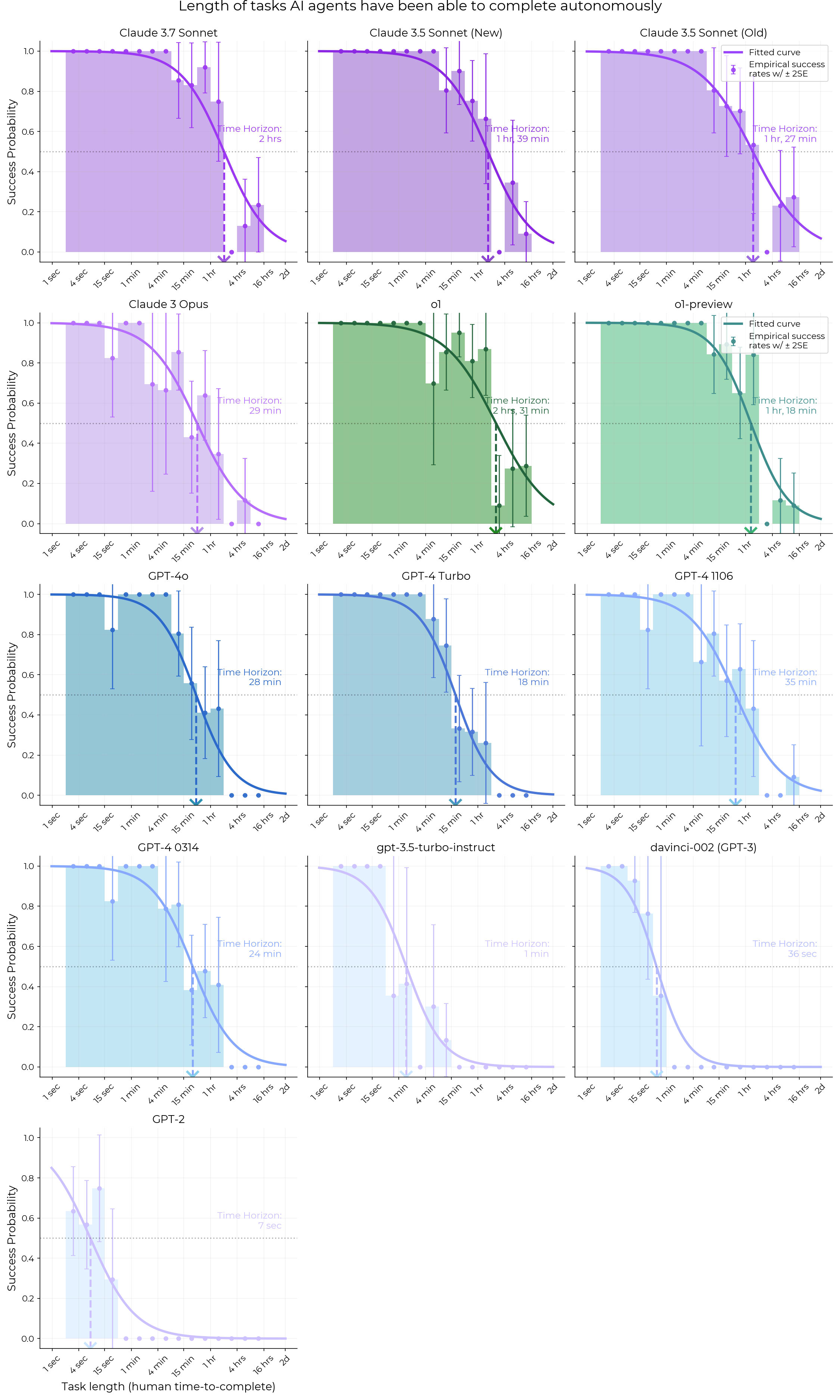
Is the recent acceleration in AI software time horizon (doubling time 7 months → 4 months) mainly due to RL, and if so is pass@8 improving slower than pass@1? If so RL could hit diminishing returns. METR already has the data to test how quickly pass@8 is improving, so I could quickly run this (edit: done, see this comment).

Thanks to @Vladimir_Nesov for mentioning this paper here.

I ran the horizon length graph with pass@8 instead, and the increase between GPT-4 and o1 seems to be slightly smaller (could be noise), and also Claude 3.7 does worse than o1. This means the doubling rate for pass@8 may be slightly slower than for pass@1. However, if horizon length increase since 2023 were only due to RL, the improvement from pass@8 would be barely half as much as the improvement in pass@1. It's faster, which could be due to some combination of the following:

o1 has a better base model than GPT-4
HCAST is an example of "emergent capabilities on long-horizon tasks", unlike their non-agentic tasks
RL helps more on HCAST skills than math or non-agentic coding
RL helps more on larger models
Some kind of nonlinearity in the relevant metrics

There are various problems with this graph (e.g. to follow the same methodology we should filter for models that are frontier on pass@8, not frontier on pass@1) but this was meant to be a quick and dirty check.

	GPT-4 horizon	o1 horizon	Ratio
Pass@8	24 min	151 min	6.3x
Pass@1	5 min	39 min	7.8x

Out of domain (i.e. on a different math benchmark) the RLed model does better at pass@256, especially when using algorithms like RLOO and Reinforce++. If there is a crossover point it is in the thousands. (Figure 7)

This seems critically important. Production models are RLed on hundreds to thousands of benchmarks.

We should also consider that, well, this result just doesn't pass the sniff test given what we've seen RL models do. o3 is a lot better than o1 in a way which suggests that RL budgets do scale heavily with xompute, and o3 if anything is better at scaling up in a Pass@N way (o3 is reported to be fully parallelizable, capable of scaling up to $1000s of compute).

Something is up here. Maybe it's lack of test-time scaling, maybe OpenAI really do have a secret RL algorithm (nobody else has demonstrates the capability to scale up test-time compute in quite in the way that o3 can). Maybe the authors just did it wrong. Maybe the authors didn't do enough RL (again, we know o3 used a lot of RL compute; the authors here only did 100s of steps)

Overall I don't buy the conclusions of that paper.

o3 is a lot better than o1 in a way which suggests that RL budgets do scale heavily with xompute, and o3 if anything is better at scaling up in a Pass@N way (o3 is reported to be fully parallelizable, capable of scaling up to $1000s of compute).

o3 may also have a better base model. o3 could be worse at pass@n for high n relative to its base model than o1 is relative to its base model, while still being better than o1.

I don't think you need very novel RL algorithms for this either - in the paper, Reinforce++ still does better for pass@256 in all cases. For very high k, pass@k being higher for the base model may just imply that the base model has a broader distribution to sample from, while at lower k the RL'd models benefit from higher reliability. This would imply that it's not a question of how to do RL such that the RL model is always better at any k, but how to trade off reliability for a more diverse distribution (and push the Pareto frontier ahead).

o3 is reported to be fully parallelizable, capable of scaling up to $1000s of compute

If you're referring to the ARC-AGI results, it was just pass@1024, for a nontrivial but not startling jump (75.7% to 87.5%). About the same ballpark as in the paper, plus we don't actually know how much better its pass@1024 was than its pass@256.

The costs aren't due to an astronomical k, but due to it writing a 55k-token novel for each attempt plus high $X/million output tokens. (Apparently the revised estimate is $600/million??? It was $60/million initially.)

(FrontierMath was pass@1. Though maybe they used consensus@k instead (outputting the most frequent answer out of k, with only one "final answer" passed to the task-specific verifier) or something.)

If you're referring to the ARC-AGI results, it was just pass@1024

It was sampling 1024 reasoning traces, but I don't expect it was being scored as pass@1024. An appropriate thing to happen there would be best-of-k or majority voting, not running reasoning 1024 times and seeing if at least one result happens to be correct.

Agree, I'm pretty confused about this discrepancy. I can't rule out that it's just the "RL can enable emergent capabilities" point.

I am not confused, the results of this paper are expected on my model.

We should also consider that, well, this result just doesn't pass the sniff test given what we've seen RL models do.

FWIW, I interpret the paper to be making a pretty narrow claim about RL in particular. On the other hand, a lot of the production "RL models" we have seen may not be pure RL. For instance, if you wanted to run a similar test to this paper on DeepSeek-V3+, you would compare DeepSeek-V3 to DeepSeek-R1-Zero (pure RL diff, according to the technical report), not to DeepSeek-R1 (trained with a hard-to-follow mix of SFT and RL). R1-Zero is a worse model than R1, sometimes by a large margin.

Another reason this could be misleading is that it's possible that sampling from the model pre-mode-collapse performs better at high k even if RL did teach the model new capabilities. In general, taking a large number of samples from a slightly worse model before mode collapse often outperforms taking a large number of samples from a better model after mode collapse — even if the RL model is actually more powerful (in the sense that its best reasoning pathways are better than the original model's best reasoning pathways). In other words, the RL model can both be much smarter and still perform worse on these evaluations due to diversity loss. But it's possible that if you're, say, trying to train a model to accomplish a difficult/novel reasoning task, it's much better to start with the smarter RL model than the more diverse original model.

“RL can enable emergent capabilities, especially on long-horizon tasks: Suppose that a capability requires 20 correct steps in a row, and the base model has an independent 50% success rate. Then the base model will have a 0.0001% success rate at the overall task and it would be completely impractical to sample 1 million times, but the RLed model may be capable of doing the task reliably.”

Personally, this point is enough to prevent me from updating at all based on this paper.

I dispute that non-update. Recall that the promise of RL isn't simply "nontrivial improvement", but "enables an RSI loop". Yes, the gain on multi-step tasks might scale exponentially with k in the corresponding pass@k. But if moving a pass@k single-step capability to pass@1 is all RL does, even improvements on multi-step tasks still hit a ceiling soon, even if that ceiling is exponentially higher than the ceiling of single-step performance improvement. And it's not clear that this potential exponential improvement actually unlocks any transformative/superhuman capabilities. ("Capabilities exponentially beyond base models'" are not necessarily very impressive capabilities.)

I'm wary of updating on this paper too much, the conclusion is too appealing and the data has some holes. But if it actually displays what it claims to display, that seems like a pretty big hit to the current Singularity-is-nigh narratives.

I don't think this follows - at the limit, any feasible trajectory can be sampled from a model with a broad distribution. Whether a model "knows" something is a pretty fuzzy question. There's a sense in which all text can be sampled by a model at high temperature, given enough samples. It's a trivial sense, except it means that moving pass@k to pass@1 for extremely high k is very non-trivial.

As an example, I took asked o4-mini the following prompt (from the OpenAI docs): "Write a bash script that takes a matrix represented as a string with format '[1,2],[3,4],[5,6]' and prints the transpose in the same format.", and fed its output into gpt-4-base (the only model I could reliably get logprobs for the input from). The average per-token logprob of o4-mini's output was -0.8998, and the average per-token logprob of gpt-4-base's top logprob continuation after each token was -0.3996. For reference, I prompted gpt-4-base with the question alone at temperature 1, and the average per-token logprob of its output was -1.8712, and the average per-token logprob of gpt-4-base's top logprob continuation after each token was -0.7218.

It seems pretty hard to dispute that o4-mini has significant improvements over a GPT-4 level model. This isn't at all at odds with the hypothesis that sampling a base model for long enough will get you arbitrarily performant outputs.

I think it's important to keep in mind the difference between the neural network and the algorithm learned by the neural network. Of any neural network, regardless of its parameters' values^[1], it's true that it's capable of outputting any sequence of tokens with some probability. But the same isn't true of all algorithms that could be learned by neural networks.

As a trivial case, consider a neural network trained to act as a calculator. Assuming the final layer is softmax as usual, is there some probability that it will output "duck" in response to "2 + 2 = "? Sure. But the "calculator" algorithm learned by the NN would never output this. Which means that if it's forced down the "duck" execution pathway, whatever is forcing it essentially breaks down the abstraction of the learned algorithm. During that forward pass, the neural substrate isn't executing the learned "calculator" algorithm; it's doing something else, it's randomly twitching.

This, I would expect, generalizes to the algorithms learned by LLMs. It is not the case that Claude-the-learned-algorithm can output any sequence of tokens, even if Claude-the-neural-network can.

E. g., suppose we receive the resolution to P vs. NP from year 3000. We then take Claude Sonnet 3.7 as it is today, and force it down the execution pathways where it recites that resolution verbatim (without being trained on it or shown it). That, I argue, would be the same as forcing a calculator LLM to output "duck". Internally, its activations during those forward passes wouldn't correspond to a possible sequence of thoughts Claude-the-learned-algorithm can think. It would correspond to some basically random activations, random mental twitches, random hallucinations/confabulations.

Thus, as we scale pass@k, there's a phase shift at some k. Up to a point, we're considering high-probability trajectories that correspond to Claude-the-learned-algorithm thinking a sequence of possible (if perhaps unlikely) thoughts. But as we scale k to, say, a googol, we start encountering trajectories during which the "Claude" abstraction broke and the NN basically behaved as a randomly initialized network.

This is the framework in which the statement "RL doesn't create capabilities, only elicits capabilities present in the base model" makes the most sense. The pretraining process creates capabilities: changes the fundamental nature of the algorithm the neural network implements. RL, on this hypothesis, only makes small changes in the context of an already-learned algorithm, tweaking its functionality but not rewriting its fundamental nature.

Which is to say: it picks the best trajectory the NN can output without violating the sanctity of the "Claude algorithm" abstraction. Which is potentially a very limited number of trajectories, combinatorially smaller than the set of all possible trajectories.

And indeed, it makes sense that it would work this way. After all, the very reason RL-as-pretraining works (whereas RL-on-randomly-initialized-networks doesn't) is because the pretrained LLM algorithm serves as a good prior for problem-solving. But if some sequence of computation/thoughts is impossible to represent in the language of that learned algorithm, if a given capability requires going beyond the functionality of that algorithm, RL is as powerless here as when applied to a random network. (Because "eliciting" that capability would require forcing a sequence of activations that "look" random from the perspective of the learned algorithm.)

Or so goes my model of that whole thing, anyway. Which papers like this one do support.

^{^}
Excepting artificial degenerate cases like "all zero".

I don't think we disagree on many of the major points in your comment. But your original claim was:

if moving a pass@k single-step capability to pass@1 is all RL does, even improvements on multi-step tasks still hit a ceiling soon, even if that ceiling is exponentially higher than the ceiling of single-step performance improvement. And it's not clear that this potential exponential improvement actually unlocks any transformative/superhuman capabilities.

The claims in the paper are agnostic to the distinction between the neural network and the algorithm learned by the neural network. It simply claims that RL makes models perform worse on pass@k for sufficiently k—a claim that could follow from the base models having a more diverse distribution to sample from.

More specifically, the paper doesn't make a mechanistic claim about whether this arises from RL only eliciting latent computation representable in the internal language of the learned algorithm, or from RL imparting capabilities that go beyond the primary learned algorithm. Outcome-based RL makes the model sample possible trajectories, and cognition outputting trajectories that are rewarded are up-weighted. This is then folded into future trajectory sampling, and future up-weighted cognition may compound upon it to up-weight increasingly unlikely trajectories. This implies that as the process goes on, you may stray from what the learned algorithm was likely to represent, toward what was possible for the base model to output at all.

I agree that if all RL ever did was elicit capabilities already known by the learned algorithm, I agree that would top out at pretty unremarkable capabilities (from a strong superintelligence perspective - I disagree that the full distribution of base model capabilities aren't impressive). But that's very different from the claim that if all RL ever did was move a pass@k capability to pass@1, it implies the same outcome.

I think that’s probably a mistake, the sentence you quoted seems to a hypothetical and the actual experimental results do seem to point against the effectiveness of current RL (?).

I am not confident though. It’s certainly true that if RL can increase the probably of a behavior/ability enough, it is not necessarily helpful to frame it as having already been in the base model’s distribution “for practical purposes.” I would have to look into this more carefully to judge whether the paper actually does a convincing job of demonstrating that this is a good frame.

Incidentally, the pass@k plots before and after RLVR (with an early intersection point) were already shown more than a year ago in the GRPO paper from Feb 2024 (Figure 7), with discussion to the same effect (Section 5.2.2):

These findings indicate that RL enhances the model’s overall performance by rendering the output distribution more robust, in other words, it seems that the improvement is attributed to boosting the correct response from TopK rather than the enhancement of fundamental capabilities.

I think the main challenge to this result is the way pass@10K performance for reasoning models keeps getting published in training papers, which would end up quite embarrassing if it turns out that pass@10K for the base models was significantly better all along. Namely, OpenAI's o1 vs. o3 paper (Figure 7, h/t ryan_greenblatt); DeepSeek-Prover-V2 and Kimina-Prover (h/t Weaverzhu).

Out of domain (i.e. on a different math benchmark) the RLed model does better at pass@256, especially when using algorithms like RLOO and Reinforce++. If there is a crossover point it might be near pass@1024. (Figure 7)

When using Reinforce++, the RL'd models perform better on pass@256 tasks as well:

That said, the curves look like the base model is catching up, and there may be a crossover point of pass@256 or the like for the in-domain tasks as well.

This could be attributable to the base models being less mode-collapsed and being able to sample more diversely. I don't think that would have predicted this result in advance however, and it likely depends on the specifics of the RL setup.

So RL “narrows the reasoning boundary”— the region of problems the model is capable of solving sometimes.

This seems useful if you don't want your model answering questions about, say, how to make bombs.

They test the perplexity (Below: Figure 6 left) of the RLed model’s generations (pink bar) relative to the base model. They find it is lower than the base model's perplexity (turquoise bar), which “suggests that the responses from RL-trained models are highly likely to be generated by the base model” conditioned on the task prompt. (Perplexity higher than the base model would imply the RLed model had either new capabilities or higher diversity than the base model.)

Does "lower-than-base-model perplexity" suggest "likely to be generated by the base model conditioned on the task prompt"? Naively I would expect that lower perplexity according to the base model just means less information per response token, which could happen if the RL-trained model took more words to say the same thing. For example, if the reasoning models have a tendency to restate substrings of the original question verbatim, the per-token perplexity on those substrings will be very close to zero, and so the average perplexity of the RL'd model outputs would be expected to be lower than base model outputs even if the load-bearing outputs of the RL'd model contained surprising-to-the-base-model reasoning.

Still, this is research out of tsinghua and I am a hobbyist, I'm probably misunderstanding something.

There's a story about trained dolphins. The trainer gave them fish for doing tricks, which worked great. Then they decided to only give them fish for novel tricks. The dolphins, trained under the old method, ran through all the tricks they knew, got frustrated for a while, then displayed a whole bunch of new tricks all at once.

Among animals, RL can teach specific skills but also reduces creativity in novel contexts. You can train creative problem solving, but in most cases, when you want control of outcomes, that's not what you do. The training for creativity is harder, and less predictable, and requires more understanding and effort from the trainer.

Among humans, there is often a level where the more capable find supposedly simple questions harder, often because they can see all the places where the question assumes a framework that is not quite as ironclad as the asker thinks. Sometimes this is useful. More often it is a pain for both parties. Frequently the result is that the answerer learns to suppress their intelligence instead of using it.

In other words - this post seems likely to be about what this not-an-AI-expert should expect to happen.

Looking at Figure 7, I think the latest intersection point for the top right plot (MATH500, RLOO) is about pass@512, while for the bottom right (MATH500, step150) it's between pass@512 and pass@1024 (and gets worse with further RL training), so probably not in the thousands.

Curated and popular this week

Read Entire Article