DumPy: NumPy except it's OK if you're dum

Note: This post includes some code that will look prettier at dynomight.net/dumpy. That also includes lots of expandy-boxes that are hard to represent here.

What I want from an array language is:

1. Don’t make me think.

2. Run fast on GPUs.

3. Really, do not make me think.

4. Do not.

I say NumPy misses on three of these. So I’d like to propose a “fix” that—I claim—eliminates 90% of unnecessary thinking, with no loss of power. It would also fix all the things based on NumPy, for example every machine learning library.

I know that sounds grandiose. Quite possibly you’re thinking that good-old dynomight has finally lost it. So I warn you now: My solution is utterly non-clever. If anything is clever here, it’s my single-minded rejection of cleverness.

To motivate the fix, let me give my story for how NumPy went wrong. It started as a nice little library for array operations and linear algebra. When everything has two or fewer dimensions, it’s great. But at some point, someone showed up with some higher-dimensional arrays. If loops were fast in Python, NumPy would have said, “Hello person with ≥3 dimensions, please call my ≤2 dimensional functions in a loop so I can stay nice and simple, xox, NumPy.”

But since loops are slow, NumPy instead took all the complexity that would usually be addressed with loops and pushed it down into individual functions. I think this was a disaster, because every time you see some function call like np.func(A,B), you have to think:

1. OK, what shapes do all those arrays have?

2. And what does np.func do when it sees those shapes?

Different functions have different rules. Sometimes they’re bewildering. This means constantly thinking and moving dimensions around to appease the whims of particular functions. It’s the functions that should be appeasing your whims!

Even simple-looking things like A*B or A[B,C] do quite different things depending on the starting shapes. And those starting shapes are often themselves the output of previous functions, so the complexity spirals.

Worst of all, if you write a new ≤2 dimensional function, then high-dimensional arrays are your problem. You need to decide what rules to obey, and then you need to re-write your function in a much more complex way to—

Voice from the back: Python sucks! If you used a real language, loops would be fast! This problem is stupid!

That was a strong argument, ten years ago. But now everything is GPU, and GPUs hate loops. Today, array packages are cheerful interfaces that look like Python (or whatever) but are actually embedded languages that secretly compile everything into special GPU instructions that run on whole arrays in parallel. With big arrays, you need GPUs. So I think the speed of the host language doesn’t matter so much anymore.

Python’s slow loops may have paradoxically turned out to be an advantage, since they forced everything to be designed to work without loops even before GPUs took over.

Still, thinking is bad, and NumPy makes me think, so I don’t like NumPy.

Here’s my extremely non-clever idea: Let’s just admit that loops were better. In high dimensions, no one has yet come up with a notation that beats loops and indices. So, let’s do this:

1. Bring back the syntax of loops and indices.

2. But don’t actually execute the loops. Just take the syntax and secretly compile it into vectorized operations.

3. Also, let’s get rid of all the insanity that’s been added to NumPy because loops were slow.

That’s basically the whole idea. If you take those three bullet-points, you could probably re-derive everything I do below. I told you this wasn’t clever.

Suppose that X and Y are 2D arrays, and A is a 4D array. And suppose you want to find a 2D array Z such that

If you could write loops, this would be easy:

import numpy as np Z = np.empty((X.shape[0], Y.shape[0])) for i in range(X.shape[0]): for j in range(Y.shape[0]): Z[i,j] = Y[j] @ np.linalg.solve(A[i,j], X[i])

That’s not pretty. It’s not short or fast. But it is easy!

So how do you do this efficiently in NumPy? Like this:

import numpy as np AiX = np.linalg.solve(A.transpose(1,0,2,3), X[None,...,None])[...,0] Z = np.sum(AiX * Y[:,None], axis=-1).T

If you’re not a NumPy otaku, that may look like outsider art. Rest assured, it looks like that to me too, and I just wrote it. Why is it so confusing? At a high level, it’s because np.linalg.solve and np.sum and multiplication (*) have complicated rules, and weren’t designed to work together to solve this particular problem nicely. That would be impossible, because there are an infinite number of problems. So you need to mash the arrays around a lot to make those functions happy.

Without further ado, here’s how you solve this problem with DumPy (ostensibly Dynomight NumPy):

import dumpy as dp A = dp.Array(A) X = dp.Array(X) Y = dp.Array(Y) Z = dp.Slot() Z['i','j'] = Y['j',:] @ dp.linalg.solve(A['i','j',:,:], X['i',:])

Yes! If you prefer, you can also use this equivalent syntax:

Z = dp.Slot() with dp.Range(X.shape[0]) as i: with dp.Range(Y.shape[0]) as j: Z[i,j] = Y[j,:] @ dp.linalg.solve(A[i,j,:,:], X[i,:])

Those are both fully vectorized. No loops are executed behind the scenes. They’ll run on a GPU if you have one.

While it looks magical, but the way this actually works is fairly simple:

1. If you index a DumPy array with a string or a dp.Range object, it creates a special “mapped” array that pretends to have fewer dimensions.

2. When a DumPy function is called (e.g. dp.linalg.solve or dp.matmul (called with @)), it checks if any of the arguments have mapped dimensions. If so, it automatically vectorizes the computation, matching up mapped dimensions that share label.

3. When you assign an array with “mapped” dimensions to a dp.Slot, it “unmaps” them into the positions you specify.

No evil meta-programming abstract syntax tree macro bytecode interception is needed. When you run this code:

Z = dp.Slot() Z['i','j'] = Y['j',:] @ dp.linalg.solve(A['i','j',:,:], X['i',:])

This is what happens behind the scenes.

a = A.map_axes([0, 1], ['i', 'j']) x = X.map_axes([0], ['i']) y = Y.map_axes([0], ['j']) z = y @ dp.linalg.solve(a, x) Z = z.unmap('i','j')

It might seem like I’ve skipped the hard part. How does dp.linalg.solve know how to vectorize over any combination of input dimensions? Don’t I need to do that for every single function that DumPy includes? Isn’t that hard?

It is hard, but jax.vmap did it already. This takes a function defined using (JAX’s version of) NumPy and vectorizes it over any set of input dimensions. DumPy relies on this to do all the actual vectorization. (If you prefer your vmap janky and broken, I heartily recommend PyTorch’s torch.vmap.)

But hold on. If vmap already exists, then why do we need DumPy? Here’s why:

import jax from jax import numpy as jnp Z = jax.vmap( jax.vmap( lambda x, y, a: y @ jnp.linalg.solve(a, x), in_axes=[None, 0, 0] ), in_axes=[0, None, 0] )(X, Y, A)

That’s how you solve the same problem with vmap. (It’s also basically what DumPy does behind the scenes.)

I think vmap is one of the best parts of the NumPy ecosystem. I think the above code is genuinely better than the base NumPy version. But it still requires a lot of thinking! Why put in_axes=[None, 0, 0] in the inner vmap and in_axes=[0, None, 0] in the outer one? Why are all the axes 0 even though you need to vectorize over the second dimension of A? There are answers, but they require thinking. Loop and index notation is better.

OK, I did do one thing that’s a little clever. Say you want to create a Hilbert Matrix with

In base NumPy you’d have to do this:

X = 1 / (np.arange(5)[:,None] + np.arange(5)[None,:] + 1) # hurr?

In DumPy, you can just write:

X = dp.Slot() with dp.Range(5) as i: with dp.Range(5) as j: X[i,j] = 1 / (i + j + 1)

Yes! That works! It works because a dp.Range acts both like a string and like an array mapped along that string. So the above code is roughly equivalent to:

I = dp.Array([0,1,2,3,4]) J = dp.Array([0,1,2,3,4,5,6,7,8,9]) X['i','j'] = 1 / (1 + I['i'] + J['j'])

See? Still no magic.

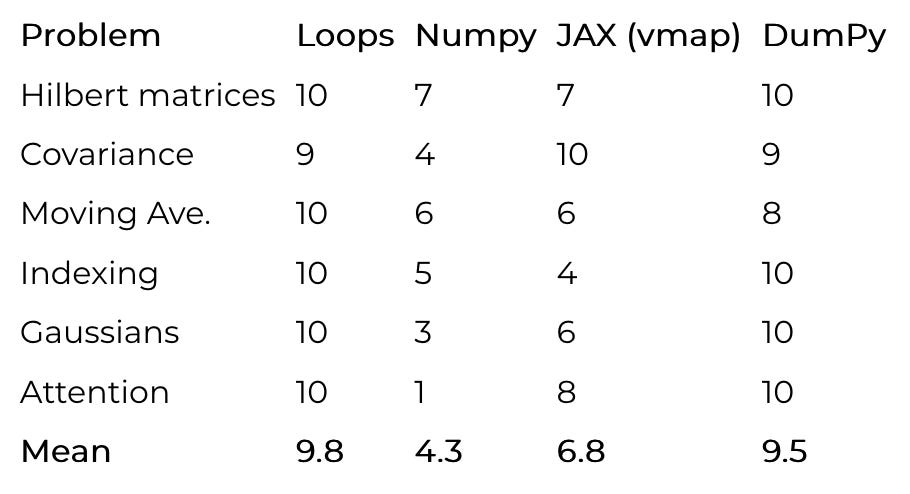
To test if DumPy is actually better in practice, I took six problems of increasing complexity and implemented each of them using loops, Numpy, JAX (with vmap), and DumPy.

• Hilbert matrices

• Batched covariance

• Moving average

• Indexing

• Gaussian Densities

• Multi-head self-attention

I gave each implementation a subjective “goodness” score on a 1-10 scale. I always gave the best implementation for each problem 10 points, and then took off points from the others based on how much thinking they required.

According to this dubious methodology and these made-up numbers, DumPy is 96.93877% as good as loops! Knowledge is power! But seriously, while subjective, I don’t think my scores should be too controversial. The most debatable one is probably JAX’s attention score.

The only thing DumPy adds to NumPy is some nice notation for indices. That’s it.

What I think makes DumPy good is it also removes a lot of stuff. Roughly speaking, I’ve tried to remove anything that is confusing and exists because NumPy doesn’t have loops. I’m not sure that I’ve drawn the line in exactly the right place, but I do feel confident that I’m on the right track, and removing stuff is good.

In NumPy, A * B works if A and B are both scalar. Or if A is 5×1×6 and B is 5×1×6×1. But not if A is 1×5×6 and B is 1×5×6×1. Huh?

In truth, the broadcasting rules aren’t that complicated for scalar operations like multiplication. But still, I don’t like it, because it adds complexity everywhere. Every time you see A * B, you have to worry about what shapes those have and what the computation might be doing.

So, I removed it. In DumPy you can only do A * B if one of A or B is scalar or A and B have exactly the same shape. That’s it, anything else raises an error. Instead, use indices, so it’s clear what you’re doing. Instead of this:

C = A[...,None] * B[None]

write this:

C['i','j','k'] = A['i','j'] * B['j','k']

Indexing in NumPy is absurdly complicated. When you write A[B,C,D] that could do many different things depending on what all the shapes are.

I considered going cold-turkey and only allowing scalar indices in DumPy. That wouldn’t have been so bad, since you can still do advanced stuff using loops. But it’s quite annoying to not be able to write A[B] when A and B are just simple 1D arrays.

So I’ve tentatively decided to be more pragmatic. In DumPy, you can index with integers, or slices, or (possibly mapped) Arrays. But only one Array index can be non-scalar. I settled on this because it’s the most general syntax that doesn’t require thinking.

Let me show you what I mean. If you see this:

# legal in both numpy and dumpy A[1, 1:6, C, 2:10]

It’s “obvious” what the output shape will be. (First the shape of 1:6, then the shape of B, then the shape of 2:10). Simple enough. But as soon as you have two multidimensional array inputs like this:

# legal in numpy, verboten in dumpy A[B, 1:6, C, 2:10]

Suddenly all hell breaks loose. You need to think about broadcasting between A and B, orthogonal vs. pointwise indices, slices behaving differently than arrays, and quirks for where the output dimensions go. So DumPy forbids this. Instead, you need to write one of these:

D['i',:,:] = A[B['i'], 1:6, C['i'], 2:10] # (1) D[:,:,'i'] = A[B['i'], 1:6, C['i'], 2:10] # (2) D['i','j',:,:] = A[B['i'], 1:6, C['j'], 2:10] # (3) D['i','j',:,:] = A[B['i','j'], 1:6, C['i'], 2:10] # (4) D['i','j',:,:] = A[B['i','j'], 1:6, C['i','j'], 2:10] # (5)

Those all do exactly what they look like they do.

Oh, and one more thing! In DumPy, you must index all dimensions. In NumPy, if A has three dimensions, then A[2] is equivalent to A[2,:,:]. This is sometimes nice, but it means that every time you see A[2], you have to worry about how many dimensions A has.

In DumPy, every index statement checks that all indices have been included. The same is true when assigning to a dp.Slot. So when you see option (4) above, you know that:

• A has 4 dimensions

• B has 2 dimensions

• C has 1 dimension

• D has 4 dimensions

Always, always, always.

Again, many NumPy functions have complex conventions for vectorization. np.linalg.solve sort of says, “If the inputs have ≤2 dimensions, do the obvious thing. Otherwise, do some extremely confusing broadcasting thing.” DumPy removes all the confusing broadcasting things. When you see dp.linalg.solve(A,B), you know that A and B have no more than two dimensions.

Similarly, in NumPy, A @ B is equivalent to np.matmul(A,B). When both inputs have ≤2 or fewer dimensions, this does the “obvious thing”. Otherwise, it does something I’ve never quite been able to remember. DumPy doesn’t need that confusing broadcasting thing, so it restricts A @ B to two or fewer dimensions.

It might seem annoying to remove features, but I’m telling you: Just try it. If you program this way, a wonderful feeling of calmness comes over you, as class after class of possible errors disappear.

Put another way, why remove all the fancy stuff, instead of leaving it optional? Because optional implies thinking! I want to program in a simple way. I don’t want to worry that I’m accidentally triggering some confusing functionality, because that would be a mistake. I want the computer to help me catch mistakes, not silently do something weird that I didn’t intend.

In principle, it would be OK if there was a evil_batch_solve method that preserves all the confusing batching stuff. If you really want that, you can make it yourself with dp.MappedFunction(jnp.linalg.solve).

Think about math: In two or fewer dimensions, coordinate-free linear algebra notation is wonderful. But for higher dimensional tensors, there are just too many cases, so most physicists just use coordinates.

So this solution seems pretty obvious to me. Honestly, I’m a little confused why it isn’t already standard. Am I missing something?

When I complain about NumPy, many people often suggest looking into APL-type languages, like A, J, K, or Q. (We’re going to run out of letters soon.) The obvious disadvantages of these are that

1. They’re unfamiliar

2. The code looks like gibberish

3. They don’t usually provide autodiff or GPU execution

None of those bother me. If the languages are better, we should learn to use them and make them do autodiff on GPUs. But I’m not convinced they are better. When you actually learn these languages, what you figure out is that the symbol gibberish basically amounts to doing the same kind of dimension mashing that we saw earlier in NumPy:

AiX = np.linalg.solve(A.transpose(1,0,2,3), X[None,...,None])[...,0] Z = np.sum(AiX * Y[:,None], axis=-1).T

If I have to mash dimensions, I want to use the best tool. But I’d prefer not to mash dimensions at all.

People also often suggest “NumPy with named dimensions” as in xarray. (PyTorch also has a half-hearted implementation.) Of course, DumPy also uses named dimensions, but there’s a critical difference. In xarray, they’re part of the arrays themselves, while in DumPy, they’re “local” and live outside the arrays.

In some cases, permanent named dimensions are very nice. But for linear algebra, they’re confusing. For example, suppose A is 2D with named dimensions "cat" and "dog". Now, what dimensions should A.T @ A have? "cat" twice? Or say you take a singular value decomposition like U, S, Vh = svd(A). What name should the inner dimensions have? Does the user have to specify that?

I haven’t seen a nice solution. xarray doesn’t focus on linear algebra, so it’s not much of an issue there. A theoretical “DumPy with permanent names” might be very nice, but I’m not how it should work. This is worth thinking about more.

I like Julia! Loops are fast in Julia! But again, I don’t think fast loops matter that much, because I want to move all the loops to the GPU. So even if I was using Julia, I think I’d want to use a DumPy-type solution.

I think Julia might well be a better host language than Python, but it wouldn’t be because of fast loops, but because it offers much more powerful meta-programming capabilities. I built DumPy on top of JAX just because JAX is very mature and good at calling the GPU, but I’d love to see the same idea used in Julia (“Dulia”?) or other languages.

OK, I promised a link to my prototype, so here it is: dumpy.py

It’s just a single file with less than 1000 lines. I’m leaving it as a single file because I want to stress that this is just something I hacked together in the service of this rant. I wanted to show that I’m not totally out of my mind, and that doing all this is actually pretty easy.

I stress that I don’t really intend to update or improve this. (Unless someone gives me a lot of money?) So please do not attempt to use it for “real work” and do not make fun of my code.