From Assumptions to Isolation: The BGKW Shift

October 30, 2025

Imagine a single, all-powerful prover, then split it in two, and forbid them to speak. In that silence, BGKW discovered that separation itself can be a source of security.

After years of research, you finally manage to prove that NP $\neq$ P, you are very excited to share your groundbreaking result. Still, before publishing it you would like to check if your proof is correct. Your first idea is to interact with one of your collegues to evaluate the correctness of the proof. However, in case the proof turns out to be false, you would still like to somehow “hide” the proof techniques from them until you can patch the proof. Formally, you become a prover, trying to convince a verifier that a statement is true, in this case “the proof is correct”. In addition to the verification, you require that your colleague learns nothing beyond the fact that the proof is correct.

As surprising as it might be, for some statements, we actually can do such proofs. In 1985, Goldwasser, Micali, and Rackoff defined these proofs as zero-knowledge proofs (as they leak $0$ bit of knowledge) and constructed one for a particular language in NP.

In 1988, Ben-Or, Goldwasser, Kilian, and Wigderson (BGKW) revealed something beautifully counterintuitive. Zero-knowledge proofs had, until then, seemed to rely on computational assumptions: limits on what an adversary could compute. BGKW showed another path, one that doesn’t weaken power, but divides it physically. By replacing a single prover with two non-communicating ones, they turned separation into a cryptographic primitive.

Through this post we will explore the notion of multi-prover interactive proofs (MIP), zero-knowledge proofs, and observe how BGKW found a new paradigm: obtaining security using the structure of the interaction rather than a computational assumption. This post is the first of a serie of blog posts which aims at explaining the techniques of BGKW. More than a formal proofs, we will slowly describe the notions that appear in BGKW and study them on their own. In a way, explaining BGKW is an excuse to explore notions that are ubiquitous in cryptography and complexity theory.

This serie will be relatively self-contained as almost all notions will be defined. However some level of familiarity with theoretical computer science is assumed. In particular, in this post, it is assumed that the reader is familiar with the notions of languages, complexity classes, and graphs.

1. From Computation to Verification: The GMR Foundation

Complexity theory is classically defined by the amount of “power” needed to compute a given function or solve a problem. However, this computational viewpoint is not always the most intuitive. In particular, non-determinism considers the existence of a computation path that leads to acceptance. One can instead think of the path as the proof, and the verifier as checking it step by step.

More concretely, NP can be defined as the set of languages $L$ for which there exists a family of proofs $\pi_L(x)$ for all $x \in L$ and a verifier $V_L$ such that for any $x \in L$, given $\pi_L(x)$ the verifier accepts, and if $x\notin L$ then for any proof $\pi$ the verifier rejects. This shift from computation verification offers a new lens for understanding complexity theory.

Graph 3-colorability

Let $L$ be the language of graphs such that there is a way to color the vertices in either red, blue or green for which no edge will be monochromatic. The language $L$ is the collection of such graphs, and the problem of $3$-colorability is to decide whether a graph $G$ is in $L$ or not (i.e., is $3$-colorable or not).

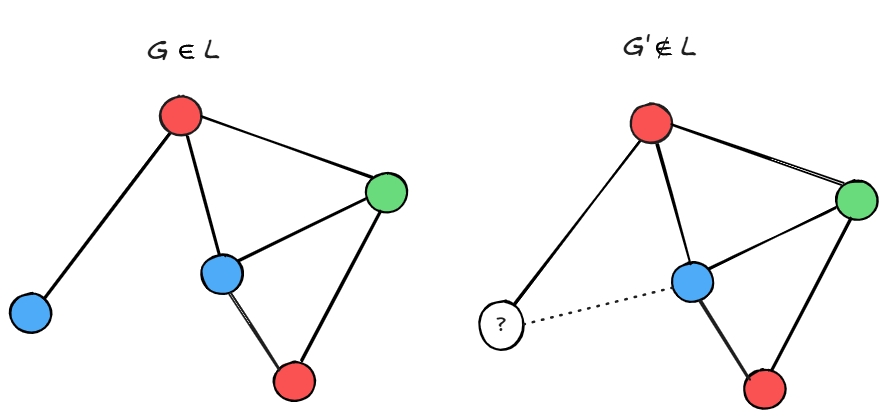
The $3$-colorability problem is in NP (and is actually NP-complete) since if $G \in L$ then there exists a path leading to acceptance: the one where the machine chooses a valid coloring and verifies it. However, if $G \notin L$ then for any $3$-coloring, there will be a monochromatic edge. In the prover–verifier model, the proof corresponds to a coloring $c$ for the graph $G$ and $V$ checks that no edge is monochromatic.

Note that in this protocol, if $G\in L$, the verifier $V$ learns a valid $3$-coloring for the graph $G$. Hence, while the proof convinces $V$ that $G$ is $3$-colorable, it reveals additional information, meaning the protocol is not zero-knowledge.

A natural extension is to allow the verifier to be randomized. This gives rise to the class MA (Merlin-Arthur), introduced by Babai in 1985, where an all-powerful Merlin provides a proof that the probabilistic verifier Arthur can efficiently check. MA is believed to be strictly larger than NP.

Merlin, ever generous with his proofs, now wishes to receive messages. So Arthur and Merlin begin an interactive protocol, the setting that defines the class IP.

In an interactive proof system, the verifier doesn’t trust the prover, it demands a convincing conversation instead. The prover might be infinitely powerful, the verifier is not. The magic lies in interaction: if the prover can answer every question in a way consistent with a valid proof, the verifier gains confidence in the claim’s truth.

This idea turned out to be quite powerful. In 1992, Shamir proved the surprising result IP=PSPACE, building on a sequence of works by Lund, Karloff, Fortnow, and Nisan.

The notion of interactive proofs was introduced earlier by Goldwasser, Micali, and Rackoff in 1985. In the same work, they introduced an even subtler concept: zero-knowledge. A zero-knowledge proof convinces the verifier that a statement is true, but reveals nothing about why. In other words, Arthur learns only that the claim holds, not any additional information. Formally, zero-knowledge is defined by requiring that whatever the verifier sees during the interaction could have been generated by itself, without the prover’s help.

Definition (Zero-Knowledge).
An interactive proof $(P,V)$ for a language $L$ is zero-knowledge if for every probabilistic polynomial-time verifier $V^*$, there exists a probabilistic polynomial-time simulator $S$ such that for all $x \in L$:

where $\text{View}_{V^*}[P(x) \leftrightarrow V^*(x)]$ is the verifier’s entire transcript of messages with the prover.

The relation $\approx$ denotes closeness of distributions:

• For perfect zero-knowledge ($\equiv$): the distributions are identical
• For statistical zero-knowledge ($\approx_s$): the distributions have negligible statistical distance
• For computational zero-knowledge ($\approx_c$): the distributions are computationally indistinguishable

The intuitive way to understand this definition is to observe that if a simulator, not possessing the knowledge of the prover, can imitate the interaction, then it must be that the message of the prover does not contain anything that requires this special knowledge. Hence, the verifier does not learn anything except that the statement is true.

To achieve zero-knowledge with a single prover, GMR relied on computational assumptions, such as the difficulty of factoring large numbers. The prover would commit to values using cryptographic primitives, and soundness followed from the assumption that the verifier couldn’t break these primitives. By 1987, Goldreich, Micali, and Wigderson had shown that zero-knowledge proofs exist for all of NP, assuming the existence of one-way functions.

Before going further in the different assumptions one can use to get security, let us explain how GMW get zero-knowledge proofs for NP. The protocol of GMW uses bit commitment as its main primitive and uses computational assumptions to build a bit commitment protocol. Bit commitment is a cryptographic primitive that allows a party $A$ to commit to a value $b$ while keeping it hidden. You can think of it as putting $b$ inside a locked chest and giving the chest to another party $B$. The scheme has two essential properties:

• Hiding: $B$ cannot learn the value of before opens the commitment.
• Binding: Once $A$ has committed, they cannot later change the value of $b$.

Later, $A$ can send the “key” to open the chest, revealing $b$ and allowing $B$ to verify it. This primitive will be the topic of a future blog post, so we will not define it formally here.

Example — Graph 3-Colorability is in ZK-IP

Let $G = (V, E)$ be a graph that the prover $P$ claims to be 3-colorable. Denote by $c : V \mapsto$ {red, blue, green} the coloring they use, and let $\pi$ be a random permutation on the colors (chosen by the prover before the protocol and kept secret from the verifier). We will write $Com(b)$ to denote the commitment of $b$ : the chest containing $b$, and $k(b)$ will be the “key” for the chest containing $b$. The protocol proceeds as follows:

1. The prover commits to his permuted coloring by sending $(Com(\pi \circ c(v_i)))_{i \leq \vert V \vert }$.
2. The verifier $V$ chooses vertices $v_1, v_2$ uniformly at random such that either $v_1 = v_2$ or $(v_1, v_2) \in E$, and sends $v_1$ to $P_1$ and $v_2$ to $P_2$.
3. $P_1$ sends $k(\pi \circ c(v_1))$ and $k(\pi \circ c(v_2))$.
4. $V$ checks that the openings are consistent with the commitment, and then accepts if and only if:
   • $\pi \circ c(v_1) = \pi \circ c(v_2)$ when $v_1 = v_2$.
   • $\pi \circ c(v_1) \neq \pi \circ c(v_2)$ when $(v_1, v_2) \in E$.

It is important to note that the zero-knowledge property obtained here is computational zero-knowledge. In fact, we will prove in another post that no bit commitment between two parties can be statistically hiding and binding. Thus, in this protocol, we use a statistically binding and computationally hiding commitment, thus leading to computational zero-knowledge.

Proving that NP $\subseteq$ ZK-IP was a remarkable achievement, but it left open a tantalizing question: must zero-knowledge depend on computational hardness? BGKW asked a different question: what if we don’t restrict the prover’s power, only divide it into two provers that could contradict each other when lying?

2. Two Rooms, One Verifier

The setup is simple to imagine and powerful to reason about. Take two provers, and put them in separate rooms, and consider the verifier as a cop. The verifier will interrogate the provers check if their answers are consistent, just like in a police questioning. The provers might have agreed on an alibi beforehand, but once inside the interrogation room, they cannot deviate from this strategy as it won’t be consistent with the other prover’s answers.

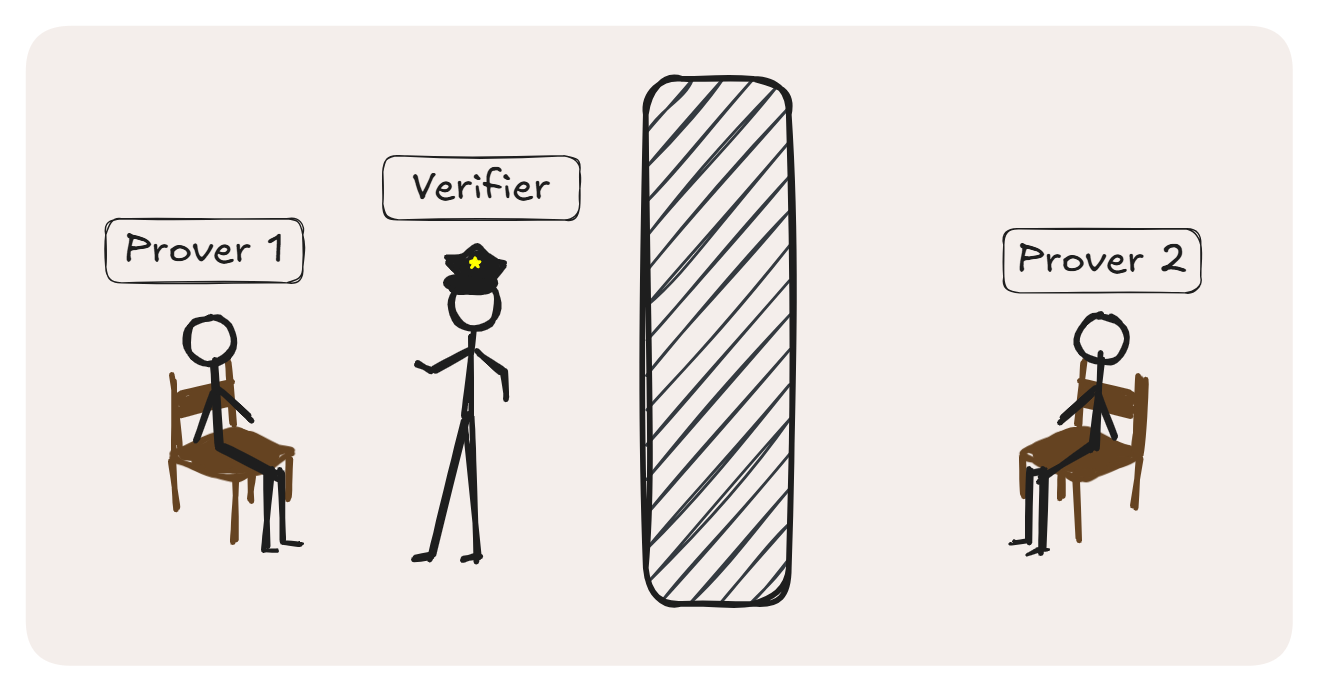
This spatial separation forces the provers into a kind of logical transparency: each must behave as if it were a consistent oracle for the same underlying proof, yet without coordination during the interaction. That constraint (no signalling, no message passing during execution) can replace computational hardness as the source of soundness.

The key insight is that honest provers can agree on a strategy beforehand and execute it flawlessly, but dishonest provers trying to prove a false statement will have to eventually give inconsistent answers when questioned separately. The verifier exploits this by asking correlated questions designed to catch any deviation from a valid proof. More formally, multi-prover interactive proofs are defined in the following way :

Definition (Multi-Prover Interactive Proof).
Let $L \subseteq \{0,1\}^*$ be a language. A k-prover interactive proof system for $L$ consists of:

• A verifier $V$ running in probabilistic polynomial time.
• $k$ provers $P_1, \dots, P_k$ that cannot communicate once the protocol starts.

The protocol defines a sequence of rounds where $V$ sends queries $q_i$ to each prover $P_i$ and receives responses $r_i$.

The system satisfies:

1. Completeness: If $x \in L$, there exist strategies for the provers so that $V$ accepts with probability $\frac{2}{3}$.
2. Soundness: If $x \notin L$, then for any strategies of the provers (including strategies coordinated before the protocol begins), $V$ accepts with probability at most $\frac{1}{3}$.

To get familiar with the multi-prover interactive proof (MIP) model and zero-knowledge, let us introduce it through a simple example of a perfect zero-knowledge MIP protocol (PZK-MIP).

Example — Graph 3-Colorability is in PZK-MIP

Let $G = (V, E)$ be a graph that the provers $P_1, P_2$ claim to be 3-colorable. Denote by $c : V \mapsto$ {red, blue, green} the coloring they use, and let $\pi$ be a random permutation on the colors (chosen by the provers before the protocol and kept secret from the verifier). The protocol proceeds as follows:

1. The verifier $V$ chooses vertices $v_1, v_2$ uniformly at random such that either $v_1 = v_2$ or $(v_1, v_2) \in E$, and sends $v_1$ to $P_1$ and $v_2$ to $P_2$.
2. $P_1$ sends $\pi \circ c(v_1)$, and $P_2$ sends $\pi \circ c(v_2)$.
3. $V$ accepts if and only if:
   • $\pi \circ c(v_1) = \pi \circ c(v_2)$ when $v_1 = v_2$.
   • $\pi \circ c(v_1) \neq \pi \circ c(v_2)$ when $(v_1, v_2) \in E$.

Completeness.
If the graph is 3-colorable, the honest provers share a valid coloring $c$. Their answers are always consistent and satisfy the verifier’s test, so the verifier always accepts.

Soundness.
If $G$ is not 3-colorable, then for any purported coloring $c$ there exists at least one monochromatic edge. The case when $v_1=v_2$ forces the provers to be consistent. Thus they need to answer according to some fixed coloring $c’$, which as mentioned before must contain a monochromatic edge. Hence, with probability at least $\frac{1}{|E|}$, when the verifier samples an edge, it might detect the inconsistency and rejects.

Perfect Zero-Knowledge.
Given any verifier $V^*$, the simulator $S$ proceeds as follows: it first samples the pair of questions $(v_1, v_2)$ according to $V^*$’s strategy, and then chooses colors $c(v_1), c(v_2)$ that satisfy the verifier’s acceptance condition. It outputs $(\pi \circ c(v_1), \pi \circ c(v_2))$, where $\pi$ is a random permutation of the three colors. Since $\pi \circ c(v_i)$ is uniformly random in {red, blue, green} conditioned on the acceptance test, the view of $V^*$ in the real interaction is identically distributed to the simulator’s output. Hence, the protocol is perfect zero-knowledge.

In the single-prover setting, we rely on a bit-commitment scheme to force the prover to fix its coloring before seeing the verifier’s question. In the multi-prover setting, this extra step isn’t needed, the separation of the provers, along with consistency checks, already ensures that their answers come from a single, consistent coloring. In other words, physics itself plays the role of the commitment.

3. What BGKW Achieved

Formally, BGKW introduced the notion of a multi-prover interactive proof (MIP) and used it to construct a perfect zero-knowledge proof for all of NEXP without any cryptographic assumptions. To be more precise, BGKW proved that MIP = perfect zero-knowledge MIP with two provers. Combining this with the independent result of Fortnow, Rompel, and Sipser, who showed that MIP = NEXP, we obtain the following theorem.

Theorem (BGKW, 1988). There exists a two-prover interactive proof system for every language in NEXP that is statistically sound and perfectly zero-knowledge, even against computationally unbounded provers.

This result was remarkable for several reasons:

1. No computational assumptions: Unlike GMR and GMW’s constructions, BGKW’s protocol achieves perfect zero-knowledge without assuming hardness of any computational problem.

2. New kind of limitation: They showed that computational limitations could be replaced by physical limitations.

3. Expressive power: Around the same time, Fortnow, Rompel, and Sipser independently showed that MIP = NEXP, demonstrating that multi-prover systems are far more powerful than single-prover systems (which capture only PSPACE).

The construction of BGKW builds on several intermediate lemmas that are of independent interest.

1. MIP(2) = MIP where MIP(2) denotes the set of languages having an MIP using only 2 provers. We will develop this technique in another blog post, but the intuitive idea to transform a $k$-prover proof into a $2$-prover proof is to have a prover $P_1$ “simulate” the $k$-prover proof, while the other prover $P_2$ serves as a consistency check: $V$ sends one question from the $k$-prover proof to $P_2$ and checks that the answer is consistent with the simulation of $P_1$.

2. Any language $L \in \textbf{MIP(2)}$ has an MIP(2) where the honest provers are always accepted. In this case we say that the MIP has perfect completeness.

3. Any perfectly complete MIP with $2$ provers can be made perfectly zero-knowledge.

Finally, combining these three lemmas gives that any language $L$ in MIP has a perfect zero-knowledge $2$ prover MIP.

4. The Shift in Perspective

BGKW didn’t just add another proof system. They reframed the nature of cryptographic security. Before them, we built security by limiting what an adversary could do. After them, we began to see security as something that could emerge from the structure of interaction itself.

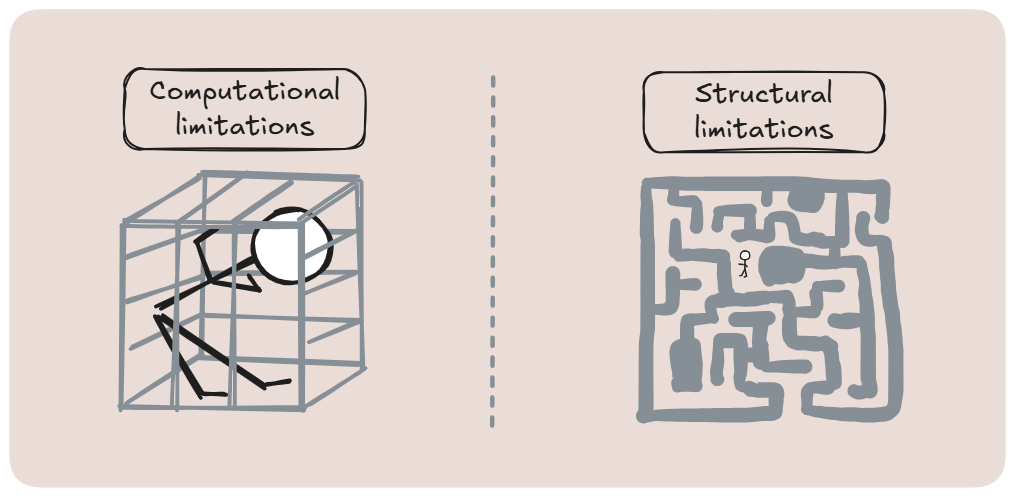
In the GMR/GMW approach, security relies on the unproven assumption that the adversary isn’t strong enough to break the bars of the cage (for example, that they cannot factor large numbers efficiently). The verifier must trust in this mathematical assumption. If the assumption one day fails (perhaps via a new algorithm or a quantum computer), the entire cage dissolves, and the security is gone.

In BGKW, the provers can be infinitely powerful, but they are trapped by the physics of the setup. The maze’s walls are the physical isolation between them. The verifier’s trust shifts from a computational assumption to a verifiable, physical constraint: the provers cannot communicate. Security is no longer based on what the provers can’t compute, but what they can’t coordinate.

This shift from computation to structure was not just a philosophical curiosity. It provided a powerful new tool. By treating isolation itself as a cryptographic primitive, BGKW unlocked a way to build protocols that don’t rely on any computational hardness assumptions.

This new perspective is the conceptual seed that would blossom into a vast array of seemingly unrelated fields. Researchers began to ask: what else can we achieve by exploiting the structure of an interaction? This line of thinking led directly to the discovery of Probabilistically Checkable Proofs (PCPs), new frontiers in quantum mechanics via non-local games, and even to the remarkable result that $\textbf{MIP}^{*}=\textbf{RE}$, connecting interactive proofs to the limits of computation itself.

5. What BGKW Opened the Way To

The BGKW framework became a cornerstone for numerous subsequent developments:

Probabilistically Checkable Proofs (PCP)

In the early 1990s, researchers realized that multi-prover interactive proofs could be reformulated as proof checking: instead of two separate provers, imagine a single static proof that the verifier queries at random locations. The key insight, developed by Babai, Fortnow, Levin, and Szegedy (1991) and culminating in the PCP Theorem by Arora-Safra (1998) and Arora-Lund-Motwani-Sudan-Szegedy (1998), was that MIP protocols could be transformed into such checkable proofs : think of the static proof as the strategy shared by the provers, and each query as a question from the verifier to a different prover of the system.

The PCP Theorem states that every language in NP has a proof that can be verified by reading only a constant number of (randomly chosen) bits. This remarkable result emerged directly from understanding the structure of multi-prover systems.

Hardness of Approximation

The PCP Theorem immediately implied hardness results for approximation problems. The connection between multi-prover proofs and combinatorial optimization problems revolutionized our understanding of which problems are hard to approximate. For instance, it showed that approximating MAX-3SAT within certain factors is NP-hard, a result whose proof became possible using MIP/PCP connection.

Non-Local Games and Quantum Foundations

In quantum information theory, multi-prover interactive proofs found an unexpected second life as non-local games. When provers share quantum entanglement, they can sometimes coordinate their answers in ways that seem impossible classically, violating Bell inequalities. Work by Cleve, Høyer, Toner, and Watrous (2004) showed that quantum strategies in non-local games can outperform any classical strategy, connecting BGKW’s framework to fundamental questions in physics.

MIP* and the Computability Frontier

Most dramatically, in 2020, Ji, Natarajan, Vidick, Wright, and Yuen proved that $\textbf{MIP}^{*}=\textbf{RE}$ (where $\textbf{MIP}^{*}$ denotes multi-prover systems where provers can share quantum entanglement, and RE is the class of recursively enumerable languages). This shocking result showed that quantum multi-prover systems can decide undecidable problems, a result with implications for the Connes embedding conjecture in operator algebras and Tsirelson’s problem in quantum mechanics.

The Power of No-Signaling Proofs

In 2013, Kalai, Raz, and Rothblum revisited the idea of isolation from a modern perspective. They defined the class $\textbf{MIP}^{\text{NS}}$, where provers are allowed arbitrary no-signaling correlations : joint strategies that forbid communication but may otherwise be non-classical (even non-quantum). They proved that $\textbf{MIP}^{\text{NS}} = \textbf{EXP}$ : under these extremely generous correlations, the system’s power collapses to exponential time as it becomes too difficult for the prover to ensure soundness. This result formalized the intuition behind BGKW: separation alone can guarantee soundness. Moreover, KRR showed how to transform such no-signaling proofs into efficient one-round delegation protocols, allowing a verifier to check exponential computations with minimal interaction. In that sense, BGKW’s “two silent provers” evolved into a general framework for delegating trust through structure.

Information-Theoretic Cryptography

BGKW’s approach inspired a broader research program in information-theoretic cryptography, where security is based on physical constraints (like non-communication, bounded storage, or noisy channels) rather than computational assumptions. This includes quantum key distribution, bounded-storage models, and secure multi-party computation with honest majorities.

Remark: Notice that the evolution of the expressive power of an MIP system according to the amount of correlation provers can use is surprising. Recall that classical strategies are included in the space of quantum strategies, which is itself included in the space of non-signaling strategies. And we have that $\textbf{MIP}=\textbf{NEXP}$, $\textbf{MIP}^{*}=\textbf{RE}$ and $\textbf{MIP}^{NS}=\textbf{EXP}$. While the difference of power between the quantum case and the other is completely unexpected, the non-monotone variation of the expressiveness is understandable. Compared to an MIP, MIP$^*$ offers more power to the provers, but not enough for them to cheat easily. However, in an $MIP^{\text{NS}}$, the provers are so powerful and correlated, that the cross-interogation technique only work for “easier” languages (in EXP).

6. The Broader Context: Where BGKW Fits

To understand BGKW’s place in the landscape of complexity theory:

Before BGKW (1985-1987):

• GMR (1985): Interactive proofs and zero-knowledge based on computational assumptions
• Babai (1985): Arthur-Merlin games, showing the power of randomness in verification
• GMW (1987): Zero-knowledge proofs for all of NP assuming one-way functions exist

BGKW (1988):

• Multi-prover interactive proofs achieving perfect zero-knowledge for NEXP without assumptions
• Fortnow-Rompel-Sipser (1988): MIP = NEXP (independent work)
• Kilian (1988) : Oblivious transfer implies oblivious circuit evaluation

After BGKW (1990s-present):

• BFLS (1991): Connection between MIP and PCPs
• AS, ALMSS (1998): PCP Theorem and hardness of approximation
• CHSH, CHTW (2004): Quantum non-local games
• KRR (2013) : MIP$^{NS}$ = EXP
• JNVWY (2020): MIP* = RE

BGKW’s paper sits at a critical juncture: it completed the foundational understanding of interactive proofs while simultaneously opening entirely new research directions that continue to yield surprises decades later.

From assumptions to isolation, BGKW’s insight continues to echo, showing that sometimes, security arises not from hardness, but from structure.

7. What Comes Next

This post sets the stage for a short series exploring how BGKW fits within the broader theory of proof systems and zero-knowledge, and diving deep into the technical machinery that makes their construction work.

Up next:

• PCPs : Why read the proof when you can roll dice ?
• Bit commitment : How to Swear Formally.
• MIP(2) = NEXP : When Two Beat One, and More Adds Nothing
• Branching Programs : Circuits are Overrated.
• Oblivious bit transfer : How to Formally Send a Message in a Bottle.
• Oblivious circuit evaluation from oblivious bit transfer : How to use Wi-Fi Outage to your Advantage.
• PZK-MIP = MIP: Zero-Knowledge Meets Multi-Prover Power.

Stay tuned, we’ll slowly build our way from this conceptual starting point to the precise mechanics of BGKW’s protocol, exploring and describing the different objects and techniques we meet along the way.

Acknowledgments: I warmly thank Arthur Pesah for his feedbacks on an earlier version of this post.

References

Foundational Papers:

1. S. Goldwasser, S. Micali, and C. Rackoff. The knowledge complexity of interactive proof systems. SIAM Journal on Computing, 18(1):186-208, 1989. (Originally appeared in STOC 1985)

2. M. Ben-Or, S. Goldwasser, J. Kilian, and A. Wigderson. Multi-prover interactive proofs: How to remove intractability assumptions. In Proceedings of STOC, 1988.

3. O. Goldreich, S. Micali, and A. Wigderson. Proofs that yield nothing but their validity or all languages in NP have zero-knowledge proof systems. Journal of the ACM, 38(3):690-728, 1991.

4. L. Fortnow, J. Rompel, and M. Sipser. On the power of multi-prover interactive protocols. Theoretical Computer Science, 134(2):545-557, 1994. (Originally appeared in Structure in Complexity Theory, 1988)

5. Joe Kilian. Founding cryptography on oblivious transfer. In 20th Annual ACM Symposium on Theory of Computing pages 20–31, 1988

6. Shamir, Adi. Ip= pspace. Journal of the ACM 39.4 (1992): 869-877

PCP and Approximation:

1. L. Babai, L. Fortnow, L. Levin, and M. Szegedy. Checking computations in polylogarithmic time. In Proceedings of STOC, 1991.

2. S. Arora and S. Safra. Probabilistic checking of proofs: A new characterization of NP. Journal of the ACM, 45(1):70-122, 1998.

3. S. Arora, C. Lund, R. Motwani, M. Sudan, and M. Szegedy. Proof verification and the hardness of approximation problems. Journal of the ACM, 45(3):501-555, 1998.

4. Y. Kalai, R. Raz, and R. Rothblum. How to Delegate Computations: The Power of No-Signaling Proofs. J. ACM, 69, 1 (2021), Article 1, 82 pages. issn:0004-5411 https://doi.org/10.1145/3456867

Quantum Extensions:

1. R. Cleve, P. Høyer, B. Toner, and J. Watrous. Consequences and limits of nonlocal strategies. In Proceedings of CCC, 2004.

2. Z. Ji, A. Natarajan, T. Vidick, J. Wright, and H. Yuen. MIP = RE.* Communications of the ACM, 64(11):131-138, 2021. (Originally appeared in arXiv:2001.04383, 2020)

Context:

1. L. Babai. Trading group theory for randomness. In Proceedings of STOC, 1985.