How the jax.jit() JIT compiler works in Jax-JS

Since the start of this year, I’ve been working on a version of JAX in pure JavaScript.

For this, I need to make a deep learning compiler from scratch, and I want to keep it lightweight (e.g., JAX uses XLA as its compiler, which is 200 KLoC — too much bundle size for the web!). This is a note about the trickiest fundamental problem I’ve run into, and how I’m going about solving it.

JAX is a great library. It takes the numerical computing properties of NumPy, shoves in GPU + Autograd, then packages it all up in a convenient API.

import jax.numpy as jnp a = jnp.array([1, 2, 3]) a * 10 # [10, 20, 30] grad(lambda x: (x * x).sum())(a) # [2, 4, 6]

By writing JAX in pure JS, using web APIs, we solve two problems:

1. How to do numerical compute in the browser? Like taking the mean of some numbers, or applying an image filter. Lots of applications, (statistics, data science, classical ML, CV, etc.), but right now it’s pretty hard to do well.

2. How do you run GPU compute in the browser? There are technologies like WebGPU if you want to write your own shaders, which is great if you’re making a video game. But this is tricky if you just want to do something simple. After all, a lot more people use PyTorch/JAX than write CUDA kernels!

No other library, ported to JS directly, would solve both problems at the same time. JAX hits the sweet spot since it’s useful for ML, and it also matches NumPy’s API.

import { grad, numpy as np } from "@jax-js/jax"; const a = np.array([1, 2, 3]); // note: type is np.Array a.mul(10); // [10, 20, 30] grad((x) => x.mul(x).sum())(a); // [2, 4, 6]

If you just want numerical computing features, import numpy as np. If you need everything else, you can pull it in as needed.

So how do you implement this? If your operations are individual CPU calls and you’re following NumPy, you would dispatch them one-by-one to a kernel. Maybe that’s a Wasm kernel for instance, and you could implement core operations like:

function neg(a: Array) { // a => -a const output = arrayLike(a); wasmBackend.dispatch("NEG:1", [a.buffer], [output.buffer]); return output; } function mul(a: Array, b: Array) { // a, b => a * b [a, b] = broadcast(a, b); const output = arrayLike(a); wasmBackend.dispatch("MUL:2", [a.buffer, b.buffer], [output.buffer]); return output; }

And then you’d have optimized Wasm kernels for each of these core operations. This is what tfjs-backend-wasm does, for instance.

But for deep learning workloads, you often want to fuse operations together. For example, let’s say you want to compute norm(x * 3 + 2) for a vector x. Doing this naively might take 4 data round-trips to the GPU or other device:

1. Compute x * 3, store the result in a.

2. Compute a + 2, store the result in b.

3. Compute b * b, store the result in c.

4. Compute sum(c), store the result in d.

5. Return sqrt(d).

For experimenting on small data, a few round trips won’t hurt anyone. But this can get painfully slow for more complex math, especially when you add in JAX-style autograd via transformations, which can increase the number of generated operations a lot.

So we’d like a way to make the operations more efficient, especially for repeated operations. This way, your browser simulation doesn’t skip frames, and your LLM produces more output tokens.

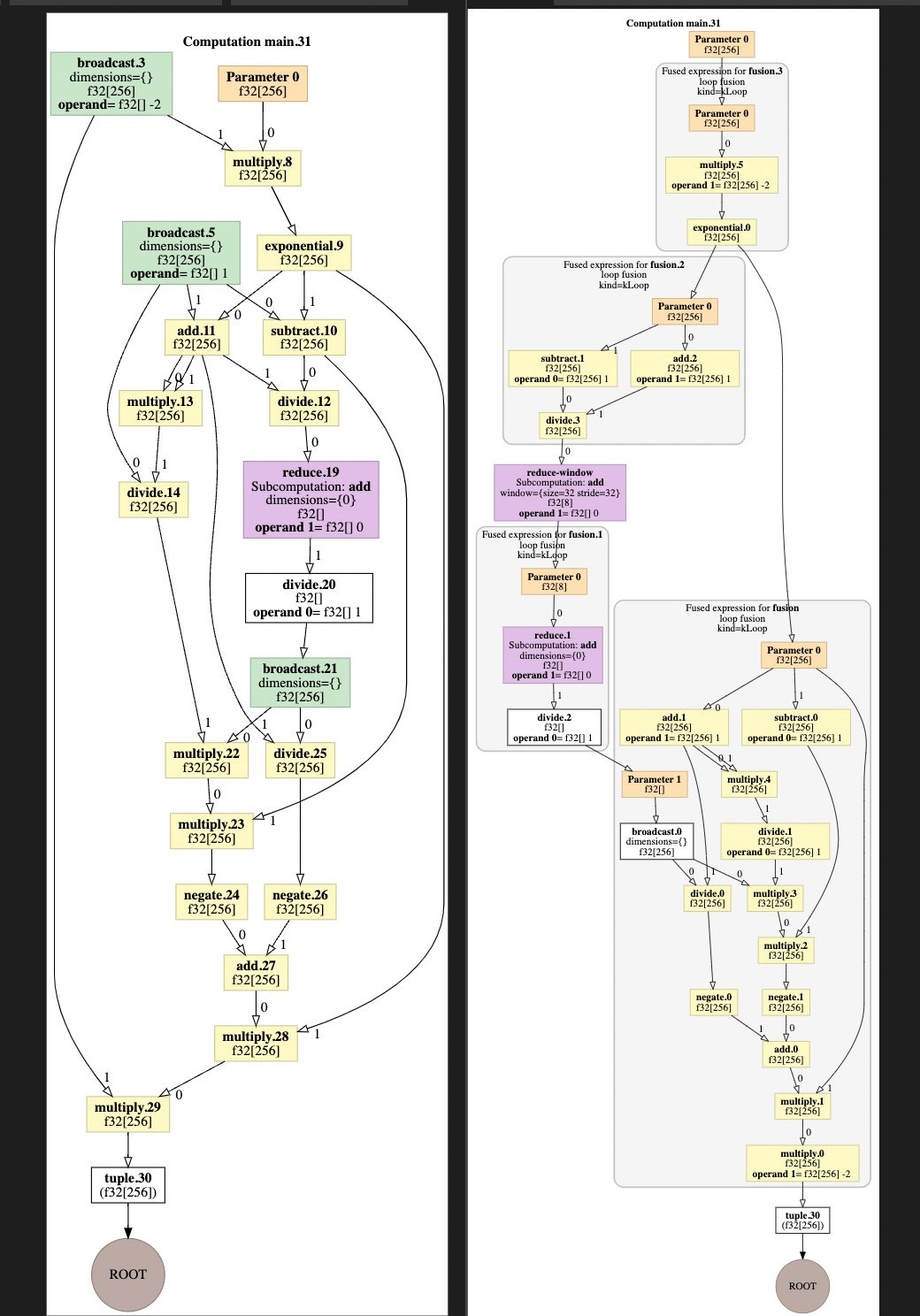
The inspiration for this JIT, or just-in-time compiler, comes from XLA, which is JAX’s backend, originating from the TensorFlow project. XLA represents computations as directed acyclic graphs (DAGs) of core primitives. Some examples:

• Exponential computes e^x.

• Multiply multiplies two numbers.

• Broadcast expands the axes of its input by repeating it.

• Reduce(Subcomputation:add) takes the sum of a tensor along some axes.

Then XLA transforms the graph on the left into the graph on the right through a series of optimization passes. In this case, several operations are turned into fused expressions, which reduces the number of round-trips and makes the overall computation ~50x faster on a T4 GPU.

Well you might say, XLA is a really high-caliber compiler, at the state of the art for ML compilation. jax-js doesn’t need to achieve top-level performance like this, since it’s running in the browser. People’s hardware / platforms are different, and it can tolerate some slack. But not 50x(!!); I think getting within 3-5x of optimal would be reasonable—so we need the JIT compiler.

(Aside: A lot of the performance difference in this case is because jax.jit() saves the graph and avoids dynamic tracing on each run, which is also relevant for us. Ignoring the dynamic tracing, I would guess the compiler alone accounts for only ~10x, maybe.)

So you need a compiler, and with compilers, you need an intermediate representation (IR) that lets you represent the computation internally. The compiler plan is to take an input, pass it through the frontend and create an IR, then optimize that IR and produce an output.

To make this work, I’m basing my IR on tinygrad, which is a very small deep learning library. The key difference between tinygrad and XLA is that tinygrad have a lot fewer primitive operations. For example, to represent a 2048x2048 matmul, the HLO would be:

HloModule jit_matmul, entry_computation_layout={(f32[2048,2048]{1,0}, f32[2048,2048]{1,0})->f32[2048,2048]{1,0}} ENTRY main.4 { Arg_0.1 = f32[2048,2048]{1,0} parameter(0) Arg_1.2 = f32[2048,2048]{1,0} parameter(1) ROOT dot.3 = f32[2048,2048]{1,0} dot(Arg_0.1, Arg_1.2), lhs_contracting_dims={1}, rhs_contracting_dims={0} }

The last line uses the primitive dot operation, which is literally just a matmul.

In contrast, tinygrad produces something more like:

a1 = a.reshape([2048, 1, 2048]) b1 = b.transpose().reshape([1, 2048, 2048]) return (a * b).sum(axis=2)

The first two lines are “movement operations” that just produce views of the data, and crucially, tracking the view can all be done within a single kernel without actually making copies. They call this laziness — but honestly I think the core thing that makes it work is not the laziness, but rather their algebra of tracking views.

So I’m taking this view-tracking system for jax-js, and it’s been working great. jax-js has an IR defined by the AluExp class, which is a (very) simplified version of tinygrad’s UOp and looks like:

/** Mathematical expression on scalar values. */ export class AluExp { constructor( readonly op: AluOp, readonly dtype: DType, readonly src: AluExp[], readonly arg: any = undefined, ) {} // ... }

An expression is fused and then is placed into a kernel, where each kernel contains at most one reduction.

/** * Description of a kernel to be compiled. * * Each of these can be processed by a backend into some lower-level * representation. It consists of one or more fused operations, optionally * indexing into a buffer. */ export class Kernel { constructor( /** Number of global arguments / arrays. */ readonly nargs: number, /** Size of the result array in element count. */ readonly size: number, /** Expression to be evaluated. */ readonly exp: AluExp, /** Optional reduction to be performed. */ readonly reduction?: Reduction, ) { this.exp = exp.simplify(); } // ... }

This gives us everything we need to implement compiler optimizations and lower IR expressions into optimized WebGPU or WebAssembly code.

Now that we have the IR done, let’s return to the actual library frontend. Recall we’ve been generating graphs of operations through JAX, which can have combinators like grad() and jvp() for automatic differentiation. So you could write an operation like log(2*x), and it would produce the computation graph for 2/(2*x) after applying the chain rule.

These graphs are almost what we need — but we need to decide when to dispatch them to the backend via Kernel objects, knowing that:

1. Each kernel fuses a common subexpression and then runs it on the GPU.

2. A kernel can have at most 1 reduction (for technical reasons; reductions are the starting point for optimizations).

A motivating example is the matmul operation, which we can try porting over:

function matmul(a: Array, b: Array) { // for clarity, assume a, b are of shape (n, n) const c = a.reshape([n, 1, n]) * b.transpose().reshape([1, n, n]); return c.sum({ axis: 2 }); }

There’s a tradeoff with this approach. tinygrad doesn’t actually do anything until you call the realize() function, which kicks off work. So it’s fine that you’re multiplying these matrices and producing c, which is of size n³, since c never actually gets realized.

jax-js tries to be a general-purpose library, so this behavior might be a bit confusing to people used to NumPy.

Luckily, we can borrow another primitive from JAX, which is the jit() function. This traces an expression, produces a “Jaxpr” or DAG of operations, and then passes it down to the ML compiler.

const matmul = jit(function matmul(a: Array, b: Array) { // for clarity, assume a, b are of shape (n, n) const c = a.reshape([n, 1, n]) * b.transpose().reshape([1, n, n]); return c.sum({ axis: 2 }); });

This opts into kernel fusion and optimization. Now, whenever the function is called with inputs of a certain shape, we get the full DAG and can run a graph algorithm to break it down into common subexpressions, each lowered into a Kernel object containing a fused AluExp.

With this, I think I’m able to offer a really fast, optimized matrix multiplication, while doing minimal work on the compiler side and keeping in line with the “spirit” of JAX: composable function transformations. There’s no need for me to write new primitives for every ML operation: like pad, fused batch normalization, and so on.

I started this project at the beginning of the year, so it’s been about 3-4 months now. At the beginning, I never thought that I would be actually implementing an ML compiler, but here we are. What makes it more manageable was a combination of:

1. Relying on JAX’s in-built JIT tracing. So composite operations like matmul(), but also anything from norm() to einsum(), can be implemented in terms of smaller parts. It gives us a clean DAG, after autograd and any combinators, to hand off to the compiler backend.

2. Borrowing tinygrad’s “view” system. This drastically simplifies the IR (see XLA’s IR for instance) and the amount of work needed to build a working library.

So that’s how jax-js is going. We’ll soon have jax.jit() support, and then some demos.

On the performance front, jax-js is already looking pretty good. It produces better matmul benchmarks than TensorFlow.js. I think landing jit() will be okay for now.

There are some unresolved questions related to memory:

• How do you do free memory? JS doesn’t have a destructor like Python does with its reference-counted __del__() method. Maybe use linear types.

• For the WebAssembly backend, how do you allocate buffers in Wasm linear memory? Generally you want to avoid fragmentation, so maybe there’s a simple way to do memory allocation here, like relying on a buddy allocator for tracking free chunks of pages.

But I’m excited about what’s coming up, since it’s almost fully usable as a numerical computing library. Some stuff I want to put in the browser soon: audio visualizers, fractals, fluid simulation, and neural audio coding. After that, I’ll open-source the library for others to try out.

If you want to keep up to date, feel free to follow me at @ekzhang1.

Hope you learned something about compilers. 🐾