Integrated photonic source of Gottesman–Kitaev–Preskill qubits

Photonic architectures for quantum computing share a common challenge: converting the classical light provided by conventional sources such as lasers into non-classical resource states that accommodate digital qubit encodings and convenient logical gate operations. High-purity sources of such states invariably rely on parametric nonlinear optical interactions and photon counting; the long and established history of quantum optics owes many of its pioneering accomplishments to spontaneous parametric downconversion and spontaneous four-wave mixing (SFWM). These mainstays of photonics provide squeezed vacuum states on demand, which are useful in their own right for quantum sensing¹³ and fundamental quantum information processing tasks¹⁴. However, further processing is required to yield useful qubit states for computation.

For linear-optical quantum computing¹⁵, the traditional processing approach is to pump the nonlinear interaction weakly and generate a two-mode squeezed vacuum state with small squeezing amplitude. Sending one output arm to single-photon detectors enables single-photon states to be heralded with low probability, offering a probabilistic source of high-purity single photons for use in dual-rail qubit encoding schemes¹⁶. Multiplexing techniques¹⁷ can then be applied to boost probabilities to sufficient levels for computation, provided optical losses associated with the multiplexer components can be mitigated. However, even with sufficiently high-probability qubit generation, implementing gate operations with single-photon dual-rail-encoded qubits is non-deterministic, leading to extra multiplexing requirements after input state synthesis. Furthermore, the single-photon detectors required to access a universal set of gates leads to nearly all components preferring integration within a cryogenic environment¹⁸.

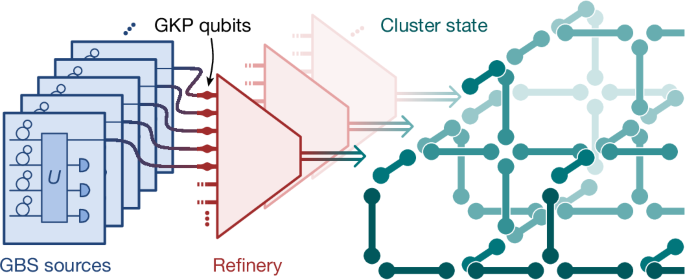
Gottesman–Kitaev–Preskill (GKP) states¹ offer a powerful alternative photonic qubit encoding that bypasses many of the challenges associated with optical quantum gate implementation. By leveraging the full infinite-dimensional Hilbert space hosted by an optical mode, qubit states can be accessed for which Clifford operations are implemented deterministically using only beamsplitters, phase shifters and homodyne detectors. Non-Clifford gates are in turn accessed through the preparation of qubit magic states². This family of states also enjoys an innate resistance against Gaussian errors, including those arising from small levels of optical loss¹⁹. Their uses extend beyond purely computation; they are promising candidates for applications in quantum communication^20,21 and sensing²². Fault-tolerant cluster states can be built deterministically from beamsplitters and sources of single-mode GKP states defined over any phase-space lattice²³. A full architecture^2,12 comprises three stages: initial state creation, refinement and cluster state synthesis, as shown in Fig. 1, with optical GKP qubit creation being the key technological bottleneck. High-quality GKP states have been reported in trapped ion^24,25 and superconducting circuit platforms^26,27,28, but their use for large-scale quantum computation in those domains does not enjoy the ease of scaling and networking available to photonic approaches¹². To fully leverage the attractive features of GKP qubits, a source of such states in the optical domain is needed.

Fig. 1: Three stages of the cluster state resource preparation for measurement-based quantum computation.

GKP qubits are generated using GBS sources. Many GBS outputs are combined at a refinery to boost the overall quality and probability of GKP sources¹². Arbitrary cluster states can be synthesized from these states deterministically using a network of beamsplitters²³. The need for scalable fabrication of GBS sources is evident for a scalable and high-quality cluster state.

Here we report the synthesis and characterization of optical GKP qubit states in the 1,550-nm wavelength band. These states show several quantitative and qualitative features that place them on a clear path to compatibility with future utility-scale fault-tolerant quantum computers. Furthermore, the techniques used to generate these states are rooted in a technological context that enables scalability to the millions of independent sources eventually required to furnish such a machine with sufficient qubits for useful applications¹². Thus, we use photonic integrated circuits manufactured on a customized silicon nitride 300-mm wafer platform using a fabrication process that was specially optimized for low optical loss, the most critical physical imperfection for these systems, while preserving the nonlinearity needed for non-classical light generation. For state heralding, we use custom efficiency-optimized transition edge sensor detectors with measured detection efficiencies as high as \(99.8{9}_{-0.53}^{+0.11} \% \), providing intrinsic photon number resolution. This convergence of advances in chip fabrication and detection, combined with techniques for rigorous optimization of programmed circuit parameters for state synthesis, produces a source of GKP qubits that we show is directly connected (after further necessary improvements in optical losses) to a device compatible with fault-tolerant operation.

The approach used in this experiment to synthesize GKP states relies on linear-optical interference to entangle four separate single-mode squeezed states, followed by heralding from photon number resolving (PNR) detection on three of the output modes using transition edge sensor detectors¹². We refer to this as a four-mode Gaussian boson sampling (GBS) source or GBS device. The level of squeezing, interferometer settings and photon detection pattern determine which state is heralded (exact settings can be found in the Supplementary Information).

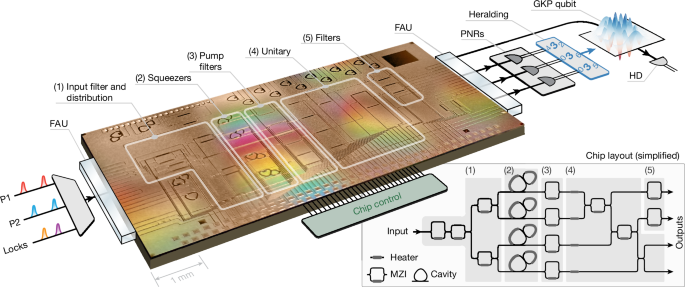
A high level schematic of the experiment is shown in Fig. 2. The chip used in this experiment was fabricated on a low-loss silicon nitride (SiN) waveguide platform and integrates all the elements necessary to prepare a multi-mode entangled Gaussian state. The chip is optically packaged using fibre array units (FAUs), and electrically packaged by wire bonding. On the chip, to produce single-mode squeezed states of light, degenerate SFWM is resonantly enhanced using an array of integrated micro-ring multiresonator devices based on a photonic molecule design optimized to suppress unwanted parasitic nonlinearities²⁹. The SFWM is pumped by pulsed light from two pump lasers (P1 and P2), input to the chip together with control light (locks) for stabilizing the micro-ring resonators and the optical phase of the generated state. Following the chip layout of Fig. 2, the light input to the chip is first filtered using an asymmetric Mach–Zehnder interferometer (MZI) to suppress noise photons at the squeezing wavelength. Using three symmetric MZIs, the pump light is distributed to the four on-chip squeezers to generate nonlinear gain consistent with 10 dB of squeezing (before loss) from each of the first two squeezers and 8 dB of squeezing (before loss) from each of the second two squeezers. The generated squeezing is near-single mode with measured Schmidt number of K = 1.12 (Supplementary Information). Following squeezing generation, the pump and resonator control light is filtered out using asymmetric MZIs and collected for monitoring and stabilization purposes. The squeezed states propagate through a linear-optical interferometer, programmed to prepare a four-mode entangled state designed for heralding GKP states. Finally, the four-mode state is coupled out of the chip. Three modes are filtered using fibre coupled wavelength division multiplexing filters and measured using PNR detection, while the remaining mode is measured using balanced homodyne detection for state tomography. To prevent pump light leaking into the homodyne detection, the first mode sent to the homodyne detector is filtered using an on-chip asymmetric MZI just before light is coupled out of the chip. Another filter is present in the second mode, allowing the experiment to be reconfigured to operate the chip as a three-mode GBS source were we to disable the first mode and use the second mode as the output mode.

Fig. 2: Schematic of experiment and simplified chip layout.

A series of pump and reference laser fields are sent over fibre to the input of an optically and electrically packaged chip. The strong classical fields are filtered and distributed (1) to an array of four squeezers based on a two-resonator photonic molecule design (2). The generated pulsed, nearly single-temporal-mode, squeezed vacuum states are separated from the pump laser light by on-chip optical filters (3), before being entangled by a programmable linear interferometer or unitary (4). Another array of integrated filters further suppresses the pump light (5). Three of the optical modes are sent to PNR detectors that, when the correct detection pattern is observed, herald the production of a GKP qubit state in the remaining optical mode, which is then analysed using homodyne detection (HD).

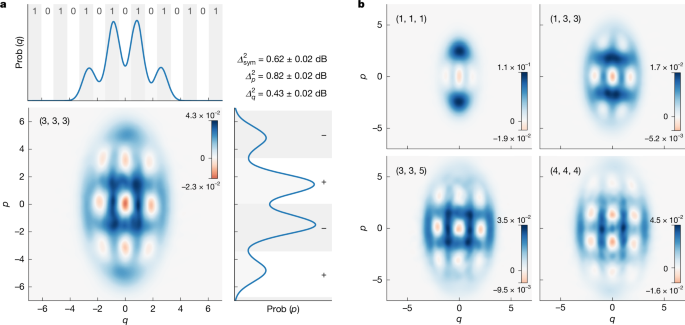
The experiment is operated at a 200 kHz repetition rate. At every repetition, the outcome of the three PNR detectors, (n₁, n₂, n₃), is recorded together with the quadrature measurement in the homodyne detection. Data from a total of 12.8 × 10⁹ repetitions are recorded and sorted by PNR outcome. We discard 20% of the noisiest PNR outcomes from each PNR detector to reduce counts from stray light (Supplementary Information), and a corresponding density matrix is then reconstructed from the quadrature measurements of the remaining PNR outcomes. The linear-optical interferometer and squeezing levels were optimized for the (3, 3, 3) PNR outcome, heralded with 2.9 × 10⁻⁴ success probability leading to a 58 Hz success rate before discarding PNR outcomes and a 0.8³ × 58 Hz ≈ 30 Hz success rate with the chosen discarding ratio. The resulting state is shown in Fig. 3a, and is a rectangular GKP state, where rectangular refers to the lattice structure of the Wigner function. In general, if one has a reconfigurable GBS device that can prepare a GKP state with one lattice, then one can always map to a new set of parameters that will produce a GKP state on a different target lattice, because the two lattices are related by a Gaussian transformation^30,31. In this device, we did not have the full reconfigurability needed to target an arbitrary lattice as, for ease of calibration, the input squeezing levels in the first two modes were constrained to be equal. Instead, we used simulations of the device (Supplementary Information) subject to that constraint to find device settings that optimized the GKP figure of merit (Methods) for the (3, 3, 3) PNR detection outcome, resulting in a rectangular lattice. Following the Z-basis convention from Gottesman et al.¹, this is equivalent to a GKP \(| 1\rangle \) state in the code space stabilized by a position shift of α and momentum shift of 4π/α, where α = 1.86. Here we have set ħ = 1 and adopt this convention throughout the remainder of this work.

Fig. 3: Experimental result.

a, Wigner function heralded by the (n₁, n₂, n₃) = (3, 3, 3) PNR outcome with position, q, and momentum, p, quadrature probability (prob) distributions and symmetric, p and q effective squeezing (\({\varDelta }_{\text{sym}}^{2}\), \({\varDelta }_{p}^{2}\), and \({\varDelta }_{q}^{2}\), respectively) shown. White and grey homodyne bins corresponding to a rectangular GKP lattice indicating probability overlap with obtaining 0/1 and +/– outcomes. The state generated is a GKP \(| 1\rangle \) state on a rectangular lattice. b, Wigner functions of a subset of heralded states for different PNR heralding pattern, (n₁, n₂, n₃): (1, 1, 1) shows a heralded cat state; (1, 3, 3), a GKP state with hexagonal lattice structure; and (3, 3, 5) and (4, 4, 4) show rectangular GKP states. States presented in a and b are reconstructed by state tomography using up to 2 × 10⁶ quadrature measurements for the (1, 1, 1) and (1, 3, 3) state, and roughly 5.9 × 10⁵, 3.6 × 10⁵ and 1.9 × 10⁶ quadrature measurements for the (3, 3, 5), (4, 4, 4) and (3, 3, 3) states, respectively. Each colour bar range shows the minimum and maximum of the corresponding Wigner function. The ħ = 1 convention is used.

Despite targeting a particular GKP state for a fixed outcome pattern of (3, 3, 3), in Fig. 3b we report examples of non-Gaussian states containing Wigner negativity heralded by other outcome patterns (see Supplementary Information for more discussion). Outcome (1, 1, 1) heralds Schrödinger cat states containing three negative regions. Outcome (1, 3, 3) heralds states with a hexagonal lattice structure. Outcome (4, 4, 4) heralds states with a 4 × 3 grid structure. We also find examples such as the (3, 3, 5) events in which the state produced has a 3 × 3 grid structure, as in Fig. 3a, and could be used in a refinery¹² to help boost the probability of GKP qubit generation (Fig. 1).

The quality of approximate GKP states can be quantified using the stabilizer expectation values (see Methods for more details). In this experiment, we produced an approximate GKP state heralded by PNR pattern (3, 3, 3) with stabilizer expectation values \(| \langle {\widehat{S}}_{p}\rangle | =0.273\pm 0.0012\) and \(| \langle {\widehat{S}}_{q}\rangle | =0.241\pm 0.002\), where \({\widehat{S}}_{p}={{\rm{e}}}^{i\alpha \widehat{p}}\), \({\widehat{S}}_{q}={{\rm{e}}}^{2{\rm{\pi }}i\widehat{q}/\alpha }\) and α = 1.86. This corresponds to effective squeezing in each quadrature of \({\varDelta }_{p}^{2}=0.82\pm 0.02\) and \({\varDelta }_{q}^{2}=0.43\pm 0.02\) dB, and symmetric effective squeezing of \({\varDelta }_{{\rm{sym}}}^{2}=0.62\pm 0.02\) dB. The uncertainties are estimated by bootstrapping (Supplementary Information). Integrating the state’s position and momentum probability distributions against the binning functions shown in Fig. 3a allows us to compute Pauli expectation values for the qubit, resulting in \((\langle \widehat{x}\rangle ,\langle \widehat{y}\rangle ,\langle \widehat{z}\rangle )=(-0.002\pm 0.002,-0.002\pm 0.0013,-0.313\pm 0.003)\) (reconstructed marginal data for Pauli-y available in the Supplementary Information). It is worth noting that the stabilizer expectation values for the state generated exceeds the simultaneous maximum, which can be achieved with a Gaussian pure state, \(| \langle {\widehat{S}}_{p}\rangle | =| \langle {\widehat{S}}_{q}\rangle | =0.208\) (Supplementary Information).

Our work delivers optical states with two key structural features that are critical for fault tolerance: both position and momentum probability distributions show four resolvable peaks, and the state has high degree of non-Gaussianity as measured by the number of negative regions in the Wigner function. Having a greater number of peaks in the q quadrature is necessary for reaching the higher p-effective squeezing (\({\varDelta }_{p}^{2}\)) values, with four peaks being in principle sufficient for reaching 10-dB quality states (and similarly for peaks in p and \({\varDelta }_{q}^{2}\)), as shown in supplementary fig. S1 of Aghaee et al.¹². Wigner negativity is a necessary resource for universal quantum computation³², and Wigner functions for GKP states consist of a lattice of positive and negative peaks in phase space¹; here we see our state achieves a 3 × 3 grid of negative Wigner regions.

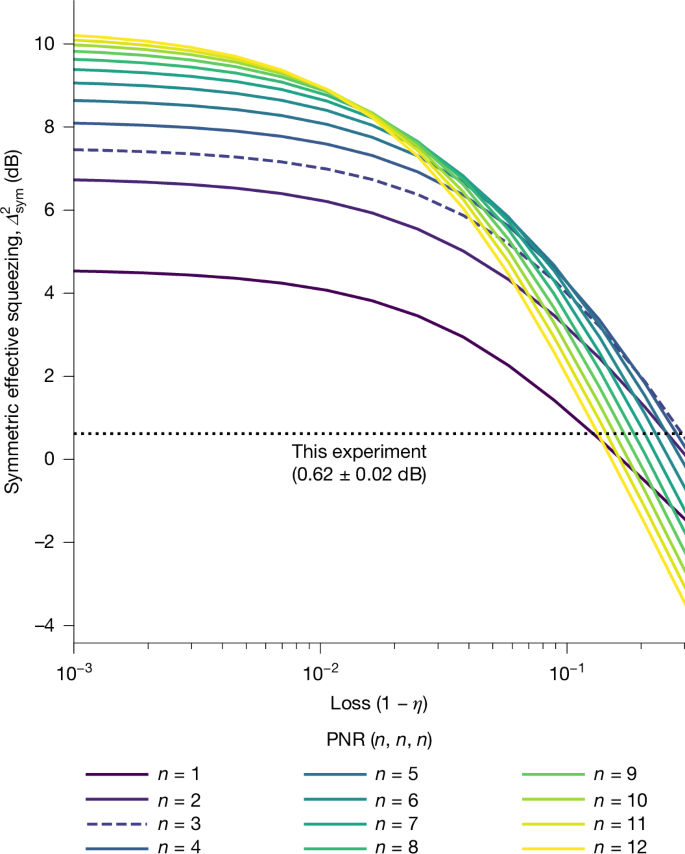
If the levels of loss were reduced further, then our simulations show that the device used in this experiment would be capable of producing states with quality sufficient for fault tolerance. The current experiment already satisfies the required number of peaks in position and momentum. Effective squeezing can be improved by reducing loss, as shown in Fig. 4. Estimates for transmission in the optical paths to the PNR detectors and to the homodyne detectors in this experiment are in the 78–82% range, resulting in the (3, 3, 3) PNR pattern yielding the highest symmetric effective squeezing. Were the end-to-end transmission, from squeezing generation to detection, to exceed around 99.5%, many PNR patterns of the form (n, n, n) with n > 7 produce GKP states with symmetric effective squeezing greater than 9.75 dB, which is the fault-tolerance threshold from Aghaee et al.¹². This is also consistent with an analysis of stellar rank (Supplementary Information).

Fig. 4: Symmetric effective squeezing versus device loss.

Symmetric effective squeezing for simulated output states of the four-mode GBS device as a function of the transmission of the heralding and heralded paths, η. Here we restrict to outcomes of the form (n, n, n) as they are among the highest quality output states. We see for transmissions in the range of 70–82% that the (3, 3, 3) outcome (dashed line) is best, as presented in this experiment. As transmission crosses 99.5%, the device is sufficient for making approximate GKP states compatible with fault tolerance.

The specific photonic circuit used in our demonstration was selected to yield a richly featured GKP state in the presence of moderate losses and without the complicating additions of further processing stages after heralding. Although we have shown that this device architecture is in principle sufficient for generating GKP states compatible with fault tolerance, the required losses would be below 1%. A more general loss-tolerant architecture was presented in Aghaee et al.¹². There it was shown that GBS devices with fewer modes (two or three) are probably preferable for a full-scale system, when many PNR outcomes are used to herald states, and multiplexing and breeding^33,34,35,36 stages are implemented after the GBS devices to boost the success probability, quality and overall loss tolerance, thereby reaching loss tolerance in the range of 1%. The four-mode GBS device architecture from our experiment is from the same ‘staircase’ family of devices presented in the supplementary section IV of Aghaee et al.¹², and could be easily modified for incorporation into a full-scale system. From Fig. 3b we see that several outcomes herald states with a grid structure. As the quality of the states produced increases, the probability could simultaneously be improved by accepting states heralded by a greater number of outcomes, with small deviations in the lattice structure being accounted for by means of measurement-based squeezing or adaptive breeding operations^12,36 (discussion in the Supplementary Information). With continuing loss reduction in chip components, fabrication and packaging, alongside development of suitable chip platforms for multiplexing and breeding, we expect future demonstrations to yield GKP qubit states of even higher quality. Our results thus illuminate an encouraging development path towards GKP qubit generation for fault-tolerant photonic quantum computers.

Here we provide experimental details on each major component in this experiment: the laser subsystem, photonic integrated chip, PNR detectors for state heralding and the homodyne detection system used for state tomography. Further details can be found in the Supplementary Information.

Laser system

The laser subsystem is composed of five lasers: two lasers (P1 and P2) for driving the dual-pump SFWM process that generates squeezing, a local oscillator laser used to perform homodyne detection and also as a frequency reference, a reference laser used to stabilize the optical phase of the quantum state and a probe laser to lock the resonance frequency of the on-chip resonators. The phase and frequency of each of these lasers are stabilized by comparing it to the local oscillator, which thus serves as a frequency and/or phase reference for the entire experiment. A portion of the local oscillator is deeply phase modulated using fibre optic phase modulators to produce an electro-optic frequency comb that spans more than 1.2 THz. Each laser is locked to one tooth of the frequency comb using an optical phase-locked loop. Using amplitude modulators, 0.5-ns pump pulses are prepared from P1 and P2, 25-ns local oscillator pulses are prepared from the local oscillator and interleaved pulses are prepared from the reference laser (20 ns) and the probe laser (100 ns). Pulses are prepared with 200 kHz repetition rate. The P1, P2 and local oscillator pulses are amplified using erbium-doped fibre amplifiers: P1 and P2 pulses are amplified to deliver 300–400 pJ to each of the four on-chip squeezers; the local oscillator is amplified to optimize homodyne detector shot noise clearance. The pulsed light is coherently distributed such that pulsed P1, P2 and a portion of the pulsed reference laser proceed to the chip, while the pulsed local oscillator and the remaining pulsed reference laser proceed to the homodyne detector. The phase of the interferometer formed by these two paths is stabilized using a fibre phase modulator by detecting the reference laser’s interference at the homodyne detector. The phase noise in this interferometer is measured independently by leaking a small portion of the local oscillator through the chip, and is measured to be 1.7° standard deviation. When combined with 1.2° standard deviation phase noise from the initial frequency and/or phase lock between P1, P2 and the local oscillator, the overall phase noise is 2.1° standard deviation.

Photonic integrated circuit

The chip was fabricated using a custom silicon nitride process, optimized for low linear loss. All samples were fabricated on 300-mm wafers using a manufacturing process that is compatible with state-of-the-art, high-volume semiconductor manufacturing (see Supplementary Information for details). The fabrication process steps were optimized to mitigate the impact of absorption and scattering losses, resulting in ultra-low propagation losses in single-mode waveguides. Reference structures are used to calibrate the loss contributions of each relevant component. Directional couplers in the filters and interferometer have roughly 4 mdB of loss, and the loss from edge coupler to SMF-28-Ultra fibre for the packaged devices is consistently less than 0.5 dB. The squeezers are based on a photonic molecule design²⁹ and are composed of a primary resonator coupled to an auxiliary resonator with a larger free spectral range (FSR). The ratio of primary FSR to auxiliary FSR is chosen to allow the resonances that would contribute to unwanted parametric nonlinear processes to be spectrally split or displaced, thereby suppressing these parasitic effects. The average loaded and intrinsic quality factors of the squeezer resonators on the chip are measured to be 3.33 × 10⁵ and 1.28 × 10⁷, respectively, corresponding to a 580-MHz full-width at half-maximum resonance bandwidth and 97.4% escape efficiency for the signal resonance. The resonances of each resonator can be independently shifted using two integrated thermo-optic phase shifters. The squeezer design is highly engineered to combine high escape efficiency, strong resonant enhancement, suppression of spurious processes and support pulsed single-temporal-mode operation. The input filter, pump filter and post-interferometer filters are all based on an asymmetric MZI design. The programmable interferometer is composed of a cascaded ‘staircase’ of tuneable couplers, with the last coupler being fixed at a 50/50 splitting ratio (see Supplementary Information for a corresponding circuit diagram). Although not universal, this arrangement has been shown to be capable of generating optical GKP qubits using the fewest optical elements (to reduce loss)¹². The first two couplers in the interferometer staircase are tunable to allow different state preparation depending on the amount of available squeezing and desired state. The chip itself is fully electro-optically packaged. The input and output waveguides are coupled to fibre array units of medium mode field diameter fibre (6.4 μm MFD, Corning HI 1060 Flex), which are then spliced to Corning SMF-28 Ultra fibre. The combined coupling efficiency from the chip waveguide to SMF-28 Ultra fibre is measured to be 0.45 dB (90%). The chip is wirebonded to a carrier printed circuit board that interfaces with the electronics required to drive the thermo-optic phase shifters and program the chip.

PNR detectors

The PNR detectors are based on a cryogenic transition edge sensor design operated in a dilution fridge at 14 mK, but can be operated at temperatures up to 50 mK (ref. ³⁷). Advancements in device fabrication, simulation, metrology and packaging have resulted in significant improvements in detection efficiency compared to results reported in the literature. The implementation of in situ spectroscopic ellipsometry measurements and new rigorous finite-difference time-domain simulations have enabled precise optimization of stack layer thicknesses during fabrication. A multifaceted metrology approach, incorporating transmission electron microscopy along with complementary techniques, has been implemented to provide comprehensive verification of the fabricated stack. Furthermore, optical packaging of the PNR detectors has been refined with improved concentricity, coupled with either a roughly 70 or 96% larger detection area compared to previously published work¹², leading to more misalignment-tolerant light coupling. The three detectors involved in the heralding operation have a measured detection efficiency of \(99.8{9}_{-0.53}^{+0.11}\), 98.40 ± 1.19 and 96.45 ± 1.04%, where uncertainties represent a 95% confidence interval (k = 2). The primary contributor to these uncertainties is the absolute calibration of the optical power meter, which has an uncertainty of 0.42% (k = 2). Many more detectors were yielded with measured detection efficiencies above 99%; the two sensors with slightly lower detection efficiency in this experiment were chosen as they had superior electrical noise performance. This characteristic is related to electronic packaging yield and is not correlated with detection efficiency. Finally, the transmissions of each wavelength division multiplexing filter before each PNR detector are measured to be 93.7, 94.1 and 94.8%.

Homodyne detection system

The homodyne detector used for state tomography is composed of a pair of high quantum efficiency photodiodes in a custom trans-impedance amplifier circuit. The quadratures of the electro-magnetic field are measured by interfering the quantum state with a strong local oscillator field on a balanced beamsplitter, detecting the two outputs with the two photodiodes and measuring the photocurrent difference. The temporal mode of the quadrature measurement is defined by the local oscillator field. Using an IQ modulator, the local oscillator field is shaped from the initial 25-ns local oscillator pulse to match the temporal mode profile of the squeezing (measured by mode tomography: Supplementary Information). The measured quadrature is defined by the relative phase between the quantum state and local oscillator. For state tomography, the local oscillator phase is varied over 32 different phase settings between 0 and π. At each phase setting, measured quadrature values are recorded for different PNR heralding events. Up to 2 × 10⁶ quadrature measurements are recorded for each heralding event. From the quadrature measurements the density matrix of the quantum state is reconstructed using maximum-likelihood techniques³⁸. The state reconstruction is done without any loss compensation, and the resulting states presented in Fig. 3 include end-to-end loss from squeezing generation to homodyne detection. We estimate the total homodyne detection efficiency to be 97%. This includes photodiode quantum efficiency (less than 99%), 21.3-dB electronic noise clearance (99.2%), mode overlap between shaped local oscillator pulse and quantum state (more than 99%) and polarization visibility (more than 99%).

Figures of merit

The defining feature of ideal GKP Pauli eigenstates is that they are eigenstates of a pair of displacements that form a parallelogram with a phase-space area 2π. For example, a rectangular lattice GKP qubit \(| 1\rangle \) is stabilized by \({\widehat{S}}_{p}={{\rm{e}}}^{i\alpha \widehat{p}}\) and \({\widehat{S}}_{q}={{\rm{e}}}^{2{\rm{\pi }}i\widehat{q}/\alpha }\), which correspond to α and 2π/α shifts in phase space along the q and p quadratures¹. For any approximate GKP state, the absolute value of the stabilizer expectation values will lie between 0 and 1, with 1 only attained by ideal GKP states. The stabilizer expectation values can be related to the effective squeezing of the peaks of the GKP state, with \({\varDelta }_{p(q)}^{2}=-\,\text{ln}(| \langle {\widehat{S}}_{p(q)}\rangle {| }^{2})/{\rm{\pi }}\) (ref. ²²). This formula can be understood as the per-peak squeezing of an approximate GKP state were it to be transformed to the lattice defined by \(\alpha =\sqrt{2{\rm{\pi }}}\) by a single-mode Gaussian unitary that implements a symplectic transformation on the phase-space lattice. This allows us to compare the quality of GKP states on different lattices³⁹. Both finite energy effects and sources of decoherence, such as photon loss, contribute to lowering the effective squeezing. We can also consider the symmetric effective squeezing, which is defined as \({\varDelta }_{{\rm{sym}}}^{2}=({\varDelta }_{p}^{2}+{\varDelta }_{q}^{2})/2\), the average variance of the peaks in both quadratures^12,39. Effective squeezing can be expressed in dB units through \(-10{\log }_{10}{\varDelta }^{2}\).

The datasets generated and analysed for this study are available at https://github.com/XanaduAI/xanadu-gkp-data.

References

Authors and Affiliations

1. Xanadu Quantum Technologies Inc., Toronto, Ontario, Canada

   M. V. Larsen, J. E. Bourassa, S. Kocsis, J. F. Tasker, R. S. Chadwick, C. González-Arciniegas, J. Hastrup, C. E. Lopetegui-González, F. M. Miatto, A. Motamedi, R. Noro, G. Roeland, R. Baby, H. Chen, P. Contu, I. Di Luch, C. Drago, M. Giesbrecht, T. Grainge, I. Krasnokutska, M. Menotti, B. Morrison, C. Puviraj, K. Rezaei Shad, B. Hussain, J. McMahon, J. E. Ortmann, M. J. Collins, C. Ma, D. S. Phillips, M. Seymour, Q. Y. Tang, B. Yang, Z. Vernon, R. N. Alexander & D. H. Mahler

Contributions

M.V.L. constructed and performed the experiment. M.V.L., S.K. and J.F.T. designed and built the experiment under the supervision of D.H.M. R.S.C., C.G.-A., J.H., C.E.L.-G., F.M.M., A.M., R.N. and G.R. provided the theory and modelling led by J.E.B. B.H. and J.M. developed the fabrication processes under the supervision of J.E.O. H.C., P.C., C.D., M.M. and C.M. designed, developed and characterized the photonic integrated chips supervised by B.M. R.B., I.D.L., M.G., T.G., C.P. and K.R.S. developed and built the photonic integrated chip package under the supervision of I.K. C.M., D.S.P., M.S., Q.Y.T. and B.Y. designed, built and tested the PNR system under the supervision of M.J.C. Z.V., R.N.A. and D.H.M. supervised the project and cowrote the manuscript with J.E.B. and M.V.L.

Corresponding author

Correspondence to D. H. Mahler.

Competing interests

The authors declare no competing interests.

Peer review information

Nature thanks Petr Marek, Alexei Ourjoumtsev and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions