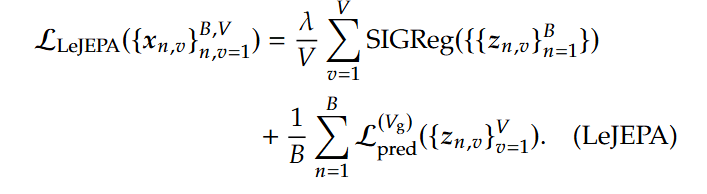Authors: Randall Balestriero, Yann LeCun
Paper: https://arxiv.org/abs/2511.08544
Code: https://github.com/rbalestr-lab/lejepa
WHAT was done? The paper introduces LeJEPA, a new self-supervised learning (SSL) framework that replaces the brittle heuristics of current Joint-Embedding Predictive Architectures (JEPAs) with a rigorous theoretical foundation. The authors first prove that the isotropic Gaussian is the unique optimal distribution for a model’s embeddings to minimize worst-case prediction risk on downstream tasks. To enforce this, they introduce a novel and highly scalable objective, Sketched Isotropic Gaussian Regularization (SIGReg), which uses random 1D projections and characteristic function matching to constrain the high-dimensional embedding space with linear time and memory complexity. The final LeJEPA objective combines a standard JEPA prediction loss with SIGReg, resulting in a lean, collapse-free training pipeline that eliminates the need for stop-gradients, teacher-student networks, and other ad-hoc fixes.
WHY it matters? LeJEPA marks a significant step in the maturation of SSL, moving the field from ad-hoc R&D to principled, provably optimal design. Its key innovations provide three major benefits:
Reliability and Simplicity: It offers exceptional training stability across diverse architectures and scales with a single trade-off hyperparameter, making foundation model pretraining more robust and accessible.
Actionable Training Signal: For the first time in JEPAs, the training loss strongly correlates (up to 99%) with downstream performance, providing a reliable, label-free signal for model selection.
New Pretraining Paradigm: It demonstrates that principled, in-domain SSL on small, specialized datasets can substantially outperform transfer learning from massive, generically-trained frontier models like DINOv2/v3, re-establishing domain-specific SSL as a viable and powerful strategy.
Joint-Embedding Predictive Architectures (JEPAs) have emerged as a promising blueprint for learning world models. This line of research is central to co-author Yann LeCun’s proposed path towards Autonomous Machine Intelligence, where the ability to predict in abstract representation space, rather than in pixel space, is seen as a key step towards building machines that can reason and plan. By predicting the representations of one part of an input from another (e.g., in an image, using a visible ‘context’ block of patches to predict the representation of a masked-out ‘target’ block), they aim to capture abstract, high-level knowledge.
However, this approach has been plagued by a persistent problem: representation collapse, where the model learns a trivial solution by mapping all inputs to the same point. To combat this, researchers have developed a complex arsenal of heuristics—stop-gradients, teacher-student networks with exponential moving averages (EMA), and explicit whitening layers—leading to training recipes that are often brittle and hard to scale.
More on JEPA ideas here:
The paper “LeJEPA” proposes a radical departure from this cycle of empirical fixes. Instead of adding another heuristic, the authors return to first principles, asking a fundamental question: what is the optimal distribution for a model’s embeddings to ensure maximum utility on future, unknown tasks? The answer to this question forms the theoretical bedrock of a new, lean, and provably stable JEPA framework.
The core theoretical contribution of the work is the rigorous proof that the isotropic Gaussian distribution is the unique optimal target for a foundation model’s embeddings (Section 3). The authors demonstrate this optimality by analyzing the risk for downstream tasks evaluated with both linear and non-linear probes.
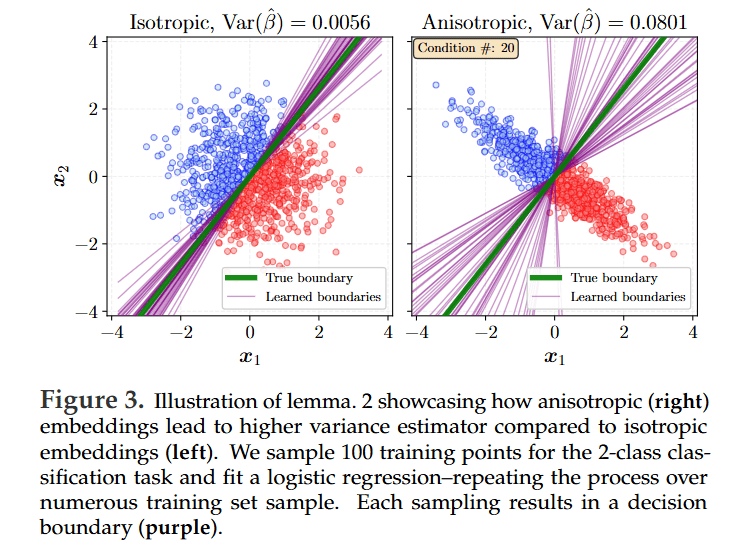
For linear probes, they show that any deviation from isotropy (i.e., an anisotropic covariance structure) amplifies both the bias (Lemma 1) and the variance (Lemma 2) of the learned downstream predictor.
For non-linear probes like k-NN and kernel methods, the isotropic Gaussian is proven to be the unique minimizer of the integrated squared bias (Theorem 1).
The intuition behind this result is powerful: an isotropic distribution, where variance is equal in all directions, makes no prior assumptions about which features will be important for future, unseen tasks. By treating all directions in the embedding space equally, it produces the most general-purpose and unbiased representations, thereby minimizing the worst-case risk when adapted to a new downstream problem.
This powerful result transforms the goal of SSL: instead of merely avoiding collapse, the objective becomes achieving a specific, provably optimal embedding geometry.
With a clear target in mind, the challenge becomes how to enforce this distribution on a high-dimensional embedding space without incurring prohibitive computational costs or training instability. The authors’ solution is a novel objective called Sketched Isotropic Gaussian Regularization (SIGReg) (Definition 2).
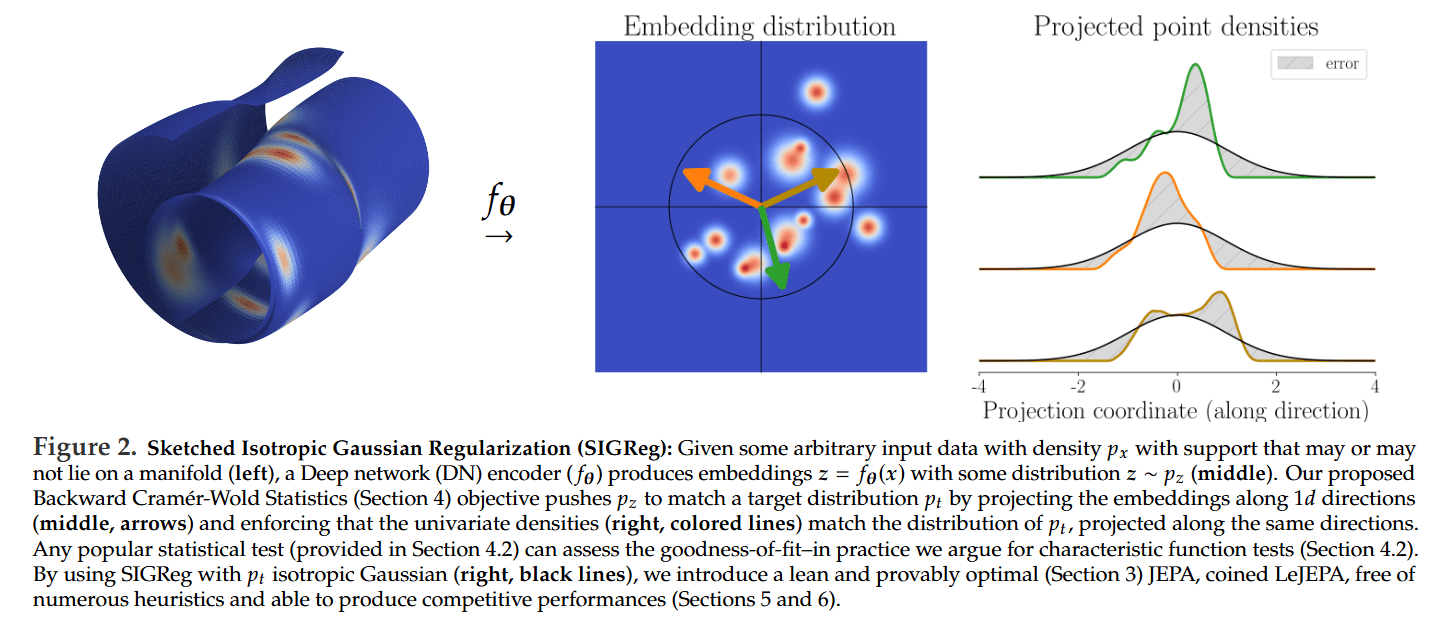
SIGReg ingeniously bypasses the curse of dimensionality by leveraging the Cramér-Wold principle. Instead of matching two high-dimensional distributions directly, it projects the embeddings onto a set of random 1D directions (”slices”) and enforces that the resulting univariate distributions match a standard 1D Gaussian (Figure 2).
The choice of the statistical test for this 1D matching is critical. The authors select the Epps-Pulley test, which is based on comparing Empirical Characteristic Functions (ECFs). This choice provides three crucial advantages over alternatives like moment-based or CDF-based tests:
Linear Complexity: It has linear O(N) time and memory complexity with respect to batch size, making it highly scalable.
Training Stability: It has provably bounded loss, gradients, and curvature, which prevents exploding gradients and ensures stable training even for massive models (Theorem 4).
Distributed-Friendly: Its formulation as a simple average is compatible with distributed training frameworks like DDP.
The final LeJEPA framework combines the standard JEPA predictive loss with the new regularization term, which is averaged across all augmented views of the input and governed by a single, robust trade-off hyperparameter λ:
This elegant formulation represents a fundamental shift from previous JEPA variants like I-JEPA. While I-JEPA relied on a predictor network, stop-gradients, and a teacher-student setup to empirically prevent collapse, LeJEPA makes these redundant. By directly enforcing the non-degenerate isotropic Gaussian distribution, the SIGReg term eliminates collapse by construction.
The results are striking: LeJEPA achieves state-of-the-art performance without a predictor, a teacher, or stop-gradients, drastically simplifying the entire training process (Table 4).
The empirical validation provides compelling evidence for the framework’s theoretical strengths.
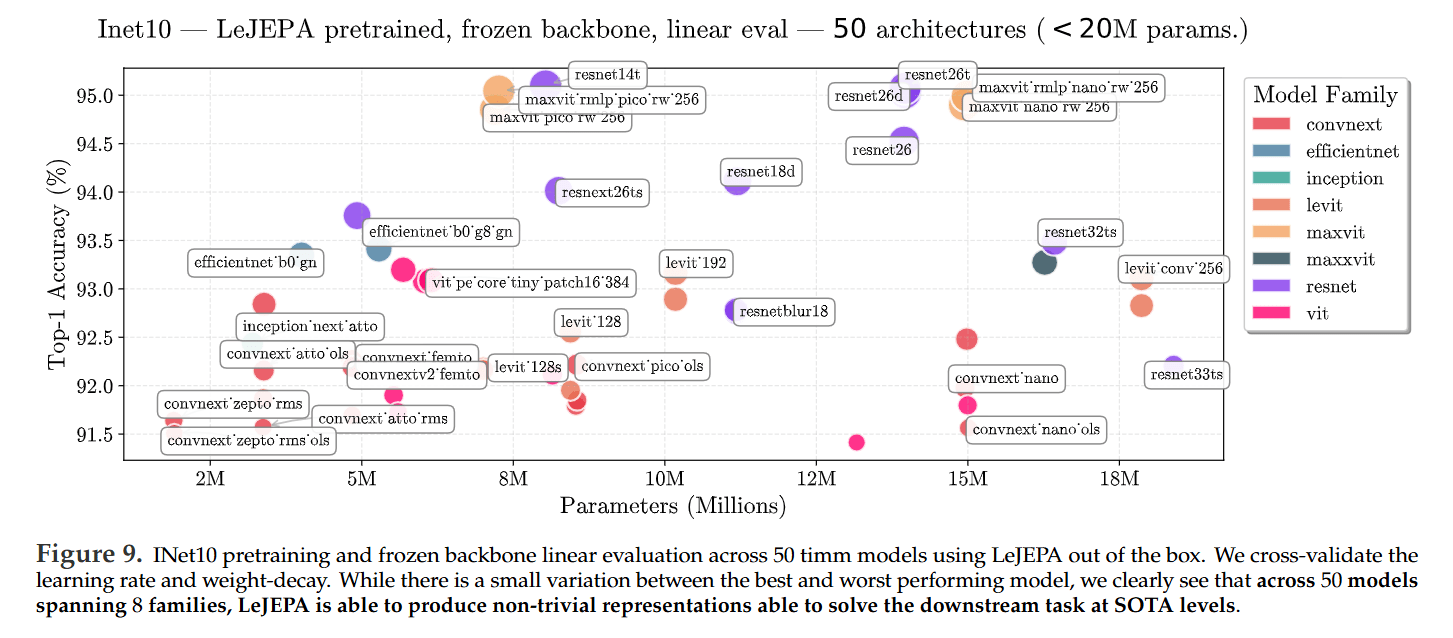
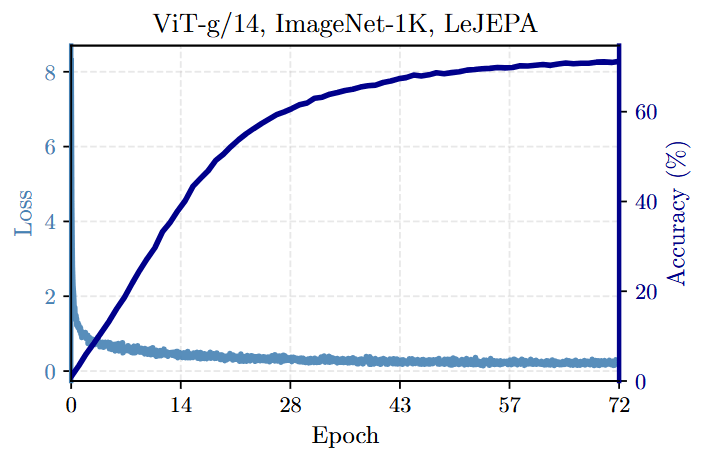
Exceptional Stability: LeJEPA demonstrates remarkable stability across over 60 architectures (Figure 9), a wide range of hyperparameters (Table 1), and scales up to a 1.8B parameter ViT-g model with a smooth training curve (Figure 1).
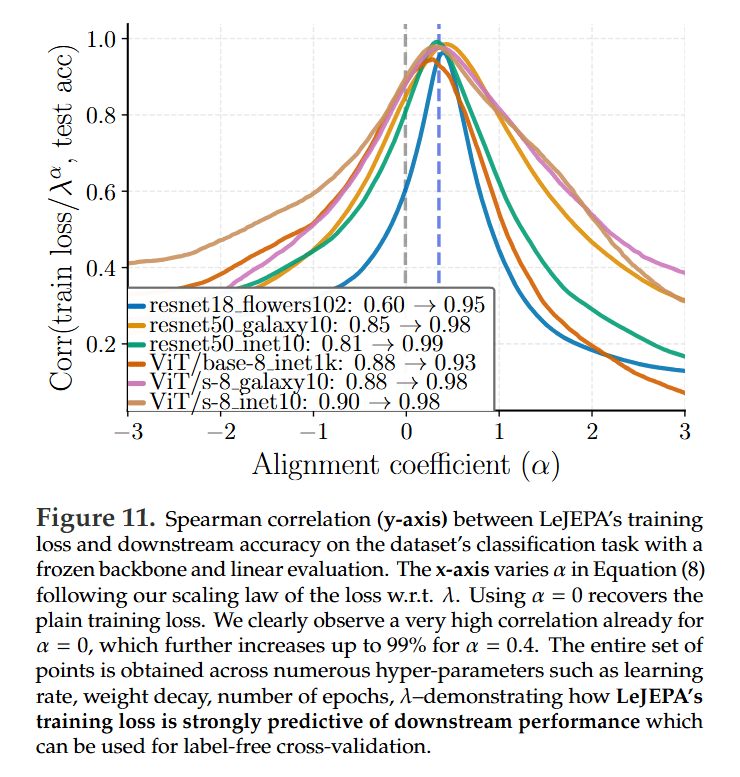
An Informative Training Loss: A significant breakthrough is that LeJEPA’s training loss is highly predictive of downstream performance. The authors show up to a 99% Spearman correlation between a scaled version of the training loss and the final linear probe accuracy (Figure 11). This provides a reliable, cheap, and label-free signal for model selection—a long-sought-after feature in SSL.
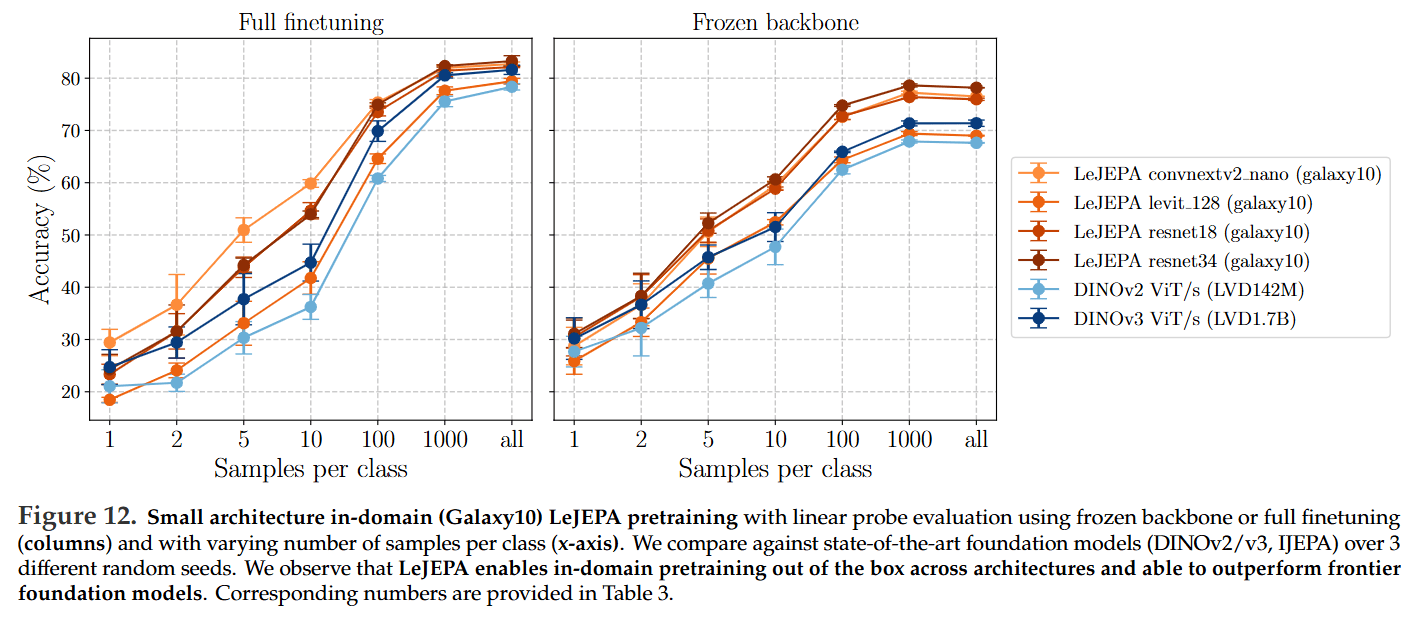
Reviving In-Domain Pretraining: Perhaps the most paradigm-shifting result is LeJEPA’s success in domain-specific pretraining. When trained from scratch on small, specialized datasets like Galaxy10 (~11k images), LeJEPA consistently and substantially outperforms transfer learning from massive frontier models like DINOv2 (https://arxiv.org/abs/2304.07193) and DINOv3 (https://arxiv.org/abs/2508.10104, review here) (Figure 12). This finding challenges the prevailing “scale is all you need” consensus and re-establishes principled, domain-specific SSL as a powerful and viable strategy, especially in data-scarce domains.
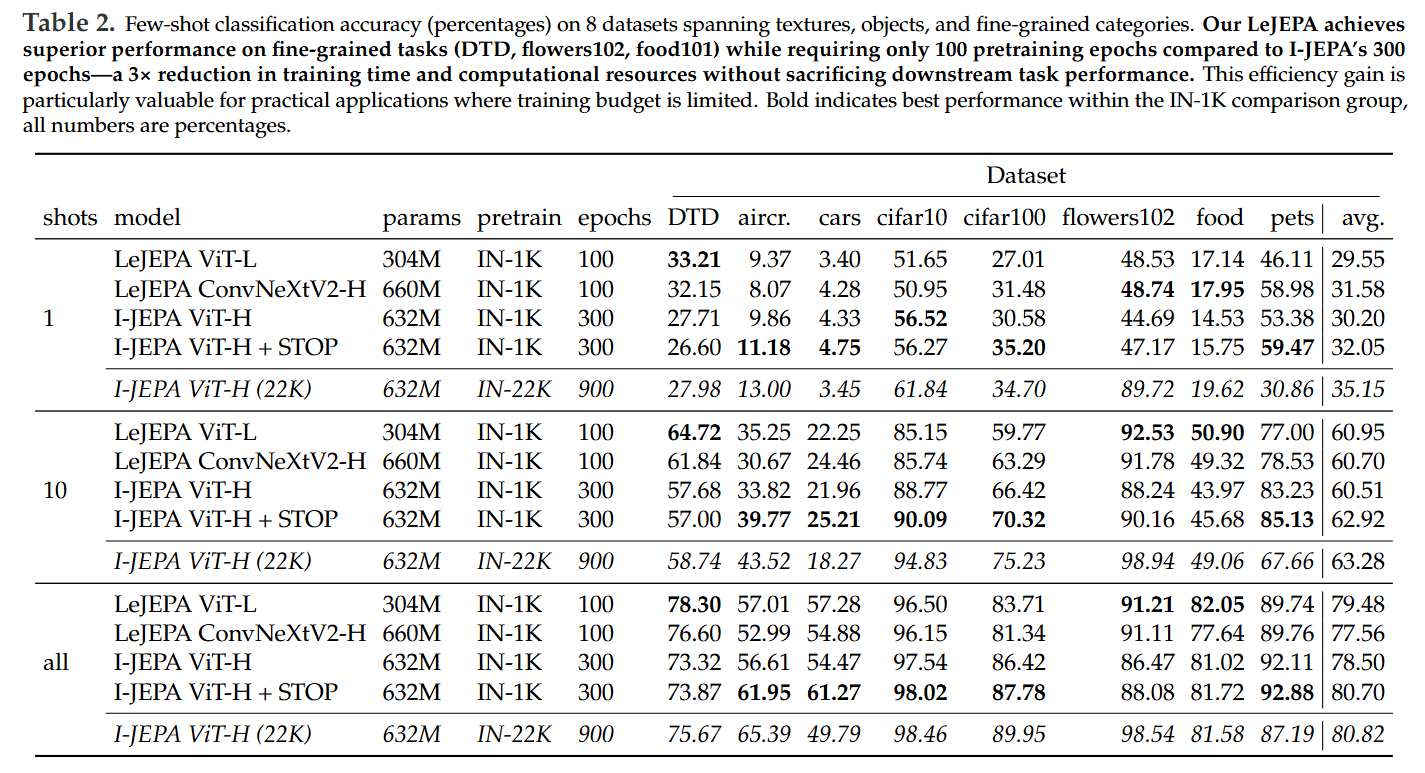
State-of-the-Art Efficiency: On ImageNet-1K, LeJEPA achieves 79% top-1 accuracy with a ViT-H/14 model and consistently matches or outperforms prior methods while often requiring significantly shorter training schedules (e.g., 100 epochs vs. I-JEPA’s 300) (Table 2).
The paper’s limitations are minor and clearly stated. The SIGReg objective has a small, well-defined bias of order O(1/N) from its minibatch implementation, for which the authors suggest future unbiased alternatives. Furthermore, while the optimality of the isotropic Gaussian is proven for minimizing worst-case risk, it remains an open question whether specific downstream tasks might benefit from structured, anisotropic geometries.
Overall, LeJEPA offers a valuable and potentially transformative contribution to the field. By grounding self-supervised learning in rigorous statistical principles, it not only solves the persistent problem of representation collapse but also delivers a framework that is simpler, more robust, and more scalable. The work provides a clear path forward, moving SSL from an art of heuristic-tuning to a science of principled optimization. This paper is a must-read for anyone involved in training foundation models.
.png)