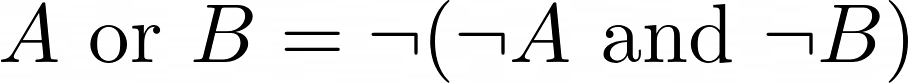Logical Reversibility of Computation

Quick intro

LeetArxiv is Leetcode for implementing Arxiv and other research papers.

In this paper, C.H Bennett (1973) introduces the concept of designing logical gates that enable reversible computing.

Reversible computing is founded on the observation that information loss in classical Boolean circuits is linked to heat dissipation (Landauer 1961). Making computing reversible leads to little heat loss, making computations more energy efficient.

This paper is canonical in the following ways :

1. Quantum computing, Thermodynamic computing and Catalytic computing are different computational paradigms stemming from the idea of reversible computers.

2. This paper motivates the design of Toffoli gates in 1980 and Fredkin gates in 1981.

The paper’s theory builds upon a 3-tape turing machine. Implementing this is not particularly useful and so, we shall spend the rest of the article coding reversible logic gates.

This section showcases truth tables for different reversible boolean gates.

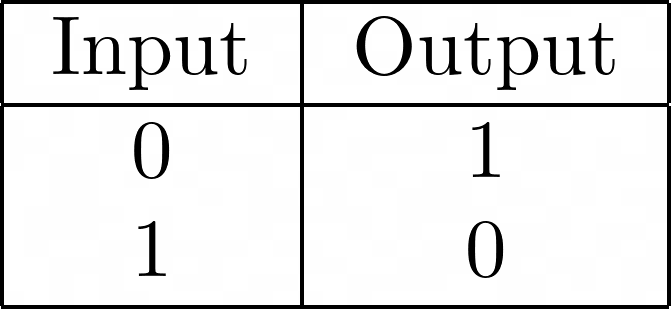
The NOT gate is reversible without any modification. This means, if one observes an output of 1 always corresponds to an input of 0.

The reversible XOR gate is the most important gate in reversible computing. (Serrano 2024)

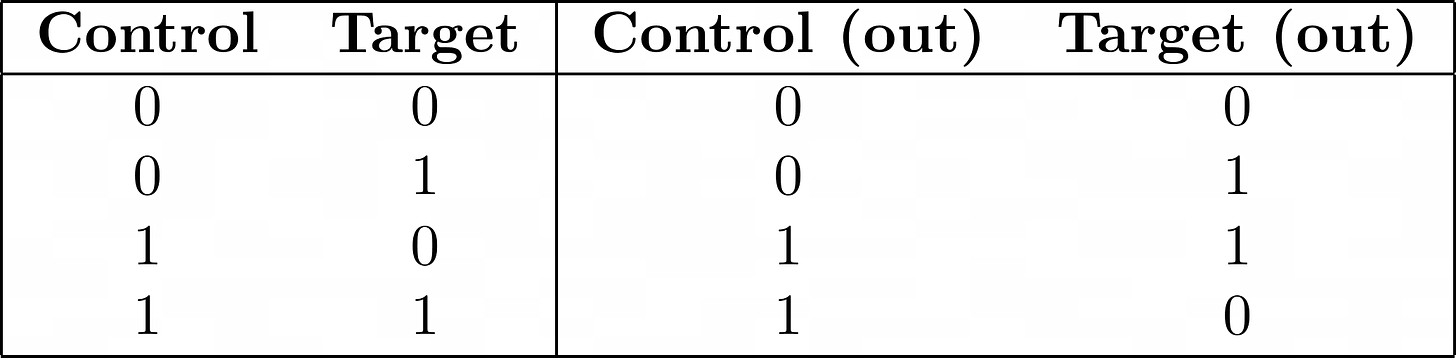
The CX gate has a control and target line. These are important things to note :

1. If control is 0 then target is not changed.

2. If control is 1 then target’s value is inverted.

3. The value of control never changes.

4. Reversing a CX gate can be done by applying a CX after.

// CX Gate Truth Table Generator function generateCXTruthTable() { // Classical bit representation const classicalInputs = [[0, 0], [0, 1], [1, 0], [1, 1]]; console.log("CX Gate Truth Table (Classical Bits):"); console.log("Ctrl | Target → Ctrl | Target"); console.log("---------------------------"); classicalInputs.forEach(input => { const [ctrl, target] = input; const output = [ctrl, ctrl === 1 ? 1 - target : target]; console.log(` ${ctrl} | ${target} → ${output[0]} | ${output[1]}`); }); // Quantum state representation console.log("\nCX Gate Truth Table (Quantum States):"); console.log("Input → Output"); console.log("------------------"); classicalInputs.forEach(input => { const [ctrl, target] = input; const output = [ctrl, ctrl === 1 ? 1 - target : target]; console.log(`|${ctrl}${target}⟩ → |${output.join('')}⟩`); }); } // Reverse CX operation by applying CX again function reverseCXTruthTable() { console.log("\nReversed CX Operation (Self-Inverse):"); console.log("Output → Original Input"); console.log("-----------------------"); const outputs = [[0, 0], [0, 1], [1, 1], [1, 0]]; // CX outputs outputs.forEach(output => { const [ctrl, target] = output; // Applying CX again returns original input const original = [ctrl, ctrl === 1 ? 1 - target : target]; console.log(`|${output.join('')}⟩ → |${original.join('')}⟩`); }); } // Run both functions generateCXTruthTable(); reverseCXTruthTable();

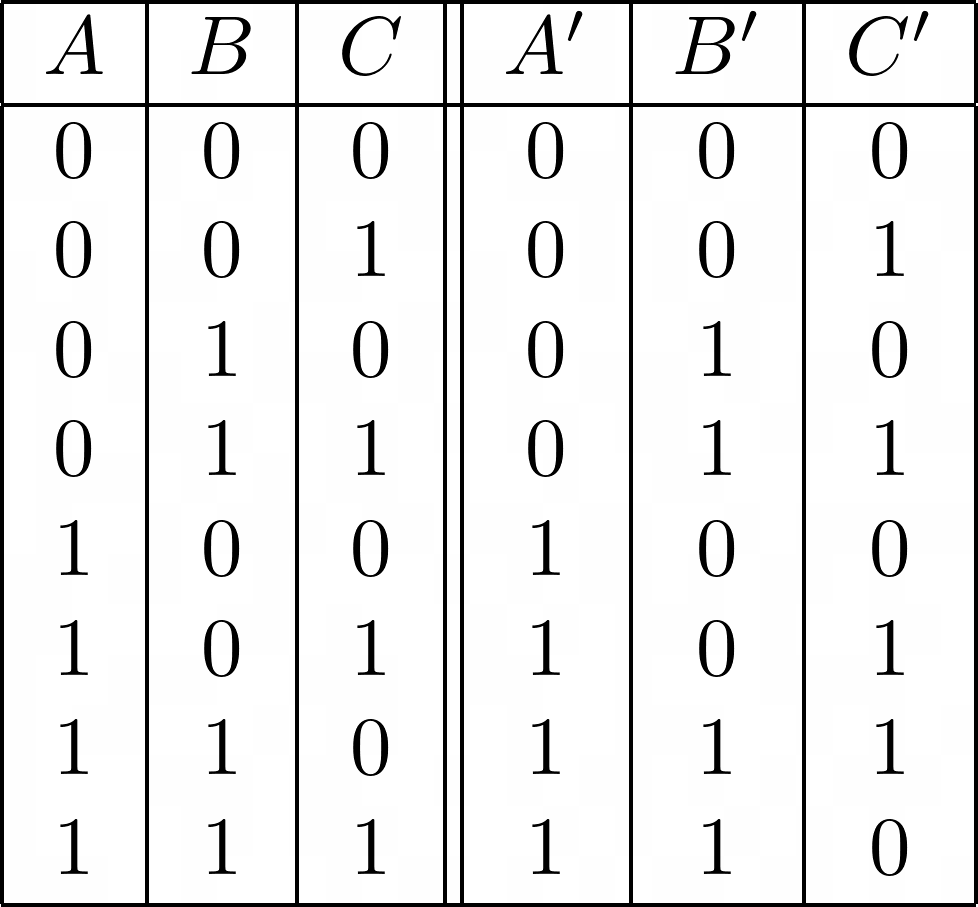
These gates were introduced by Thomas Toffoli. They take three inputs and output three boolean values.

Just like the XOR gate, reversing the Toffoli gate is by applying it twice.

*Note that we include Reversible NAND gates

When C = 0, this is AND while C = 1 is a NAND gate.

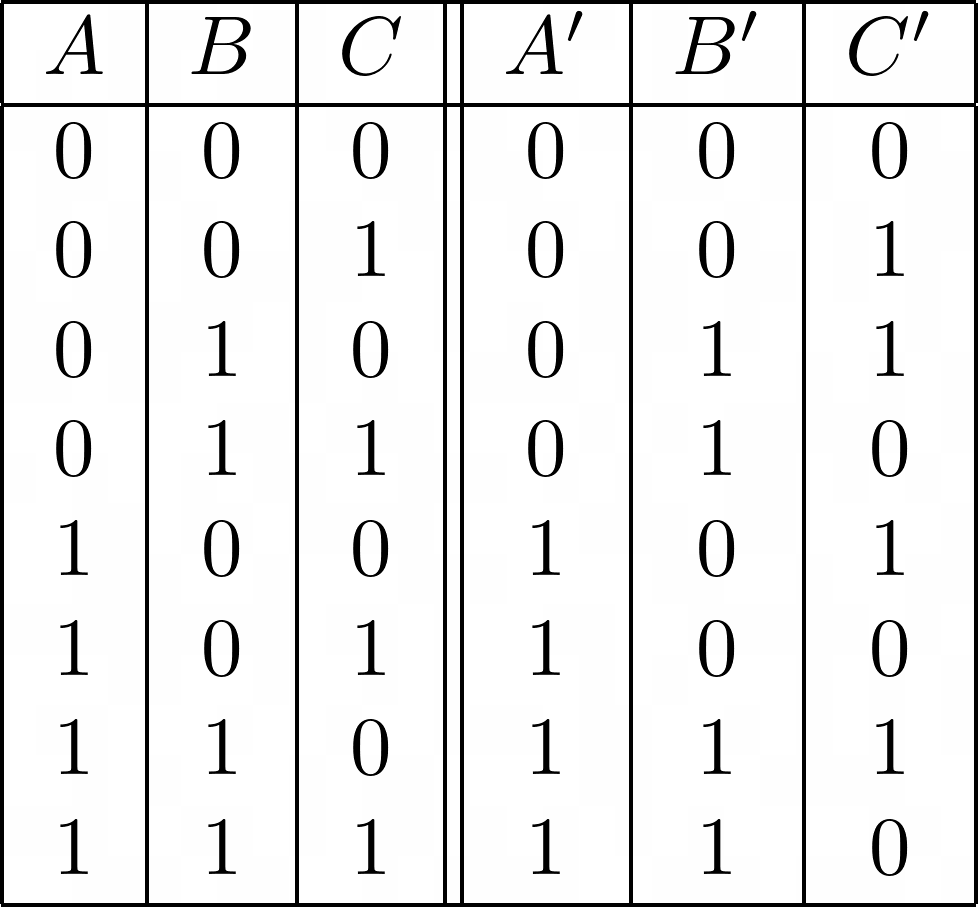
function toffoliGate(A, B, C) { // Ensure inputs are 0 or 1 if (![0, 1].includes(A) || ![0, 1].includes(B) || ![0, 1].includes(C)) { throw new Error("Inputs must be 0 or 1"); } const A_out = A; const B_out = B; const C_out = C ^ (A & B); // C' = C XOR (A AND B) return [A_out, B_out, C_out]; } // Example: print all combinations for (let A = 0; A <= 1; A++) { for (let B = 0; B <= 1; B++) { for (let C = 0; C <= 1; C++) { const [A_out, B_out, C_out] = toffoliGate(A, B, C); console.log(`A=${A}, B=${B}, C=${C} => A'=${A_out}, B'=${B_out}, C'=${C_out}`); } } }

This is the final gate we need to implement. We can build a classical boolean OR gate using NAND gates.

Using Toffoli gates, we get this truth table :

In JavaScript, this can be implemented as :

function reversibleOr(A, B, C) { // Validate inputs: must be binary (0 or 1) if (![0, 1].includes(A) || ![0, 1].includes(B) || ![0, 1].includes(C)) { throw new Error("Inputs A, B, and C must be 0 or 1"); } const A_out = A; const B_out = B; const C_out = C ^ (A | B); // C' = C XOR (A OR B) return [A_out, B_out, C_out]; } // Example: Print all 8 possible input combinations for (let A = 0; A <= 1; A++) { for (let B = 0; B <= 1; B++) { for (let C = 0; C <= 1; C++) { const [A_out, B_out, C_out] = reversibleOr(A, B, C); console.log(`A=${A}, B=${B}, C=${C} => A'=${A_out}, B'=${B_out}, C'=${C_out}`);

On the final page Bennet claims that DNA replication through the RNA polymerase can be seen as a thermally activated chemical copying Turing machine. (Hurst 2018)

He makes further claims on noise emerging as a problem in thermodynamic computing.

We have enough gates to build reversible computing algorithms. This is where paths diverge. From here, one can choose to focus on :

1. Quantum computing.

2. Catalytic computing.

3. Thermodynamic computing.

Cited as

Kibicho, Murage. (May 2025). Coding Guide Logical Reversibility of Computation. https://leetarxiv.substack.com/p/logical-reversibility-of-computation.

or

@article{Kibicho2025CodingGuideLogicalReversibilityofComputation, title = "Coding Guide Logical Reversibility of Computation", author = "Kibicho, Murage", journal = "LeetArxiv", year = "2025", month = "May", url = "https://leetarxiv.substack.com/p/logical-reversibility-of-computation" }