This document describes how TeXmacs deals with the typesetting of
mathematics, and in particular with the low level implementation of
the typesetting primitives relative to mathematical documents. It
should be useful if you are interested in understanding the C++
sources. We describe the state of facts as per svn
revision r14561 (December 2024, TeXmacs 2.14+).
Excerpts from the official documentation are included in this document
for completeness.
1.Overview
In this chapter we describe the algorithms used by TeXmacs in order to
typeset mathematical formulas. This is a difficult subject, because
esthetics and effectiveness do not always go hand in hand. Until now,
TeX is widely accepted for having achieved an optimal compromise in this
respect. Nevertheless, we thought that several improvements could still
be made, which have now been implemented in TeXmacs. We will shortly
describe the motivations behind them.
In order to obtain esthetic formulas, what criteria should we use? It is
often stressed that good typesetting allows the reader to concentrate on
what he reads, without being distracted by ugly typesetting details.
Such distracting details arise when distinct, though similar parts of
text are typeset in a non uniform way:
Different base lines
The eye expects text of a similar nature to be typeset with
respect to a same base line. For instance, in  , the bottoms of the
, the bottoms of the  and
and  should be at the same height as the
bottom of the
should be at the same height as the
bottom of the  -part in
the
-part in
the 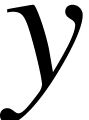 . This should again
be the case in
. This should again
be the case in 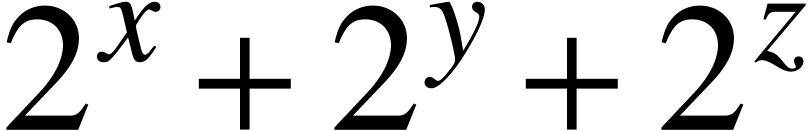 .
.
Unequal spacing
Different components of text with approximately the same function
should be separated by equal amounts of space. For instance, in
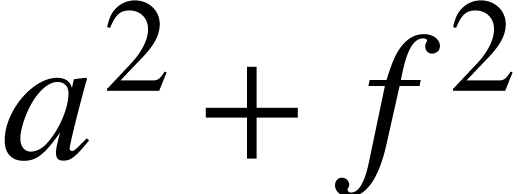 , the typesetter should
notice the hangover of the
, the typesetter should
notice the hangover of the 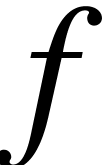 .
This should again be the case in
.
This should again be the case in 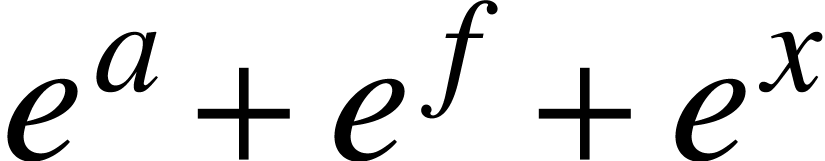 .
Similarly, the distance between the baselines of the
.
Similarly, the distance between the baselines of the  and the
and the  in
in 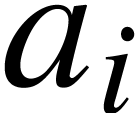 should not be disproportionally large with respect to the height
of an
should not be disproportionally large with respect to the height
of an  .
.
Additional difficulties may arise when considering automatically
generated formulas, in which case line breaking has to be dealt with in
a satisfactory way.
Unfortunately, the different esthetic criteria may enter into conflict
with each other. For instance, consider the formula 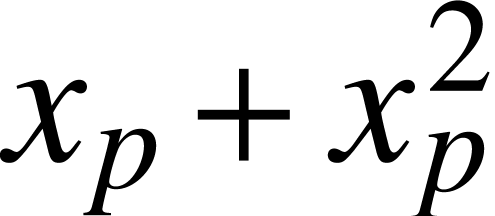 . On the one hand, the baselines of the scripts
should be the same, but the other hand, the first subscript should not
be “disproportionally low” with respect to the
. On the one hand, the baselines of the scripts
should be the same, but the other hand, the first subscript should not
be “disproportionally low” with respect to the  . Unfortunately, this dilemma can not been
solved in a completely satisfactory way without the help of a human for
the simple reason that the computer has no way to know whether the
. Unfortunately, this dilemma can not been
solved in a completely satisfactory way without the help of a human for
the simple reason that the computer has no way to know whether the 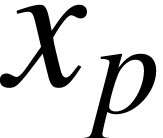 and
and 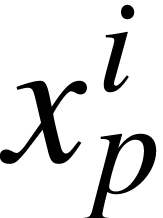 are
“related”. Indeed, if the
are
“related”. Indeed, if the 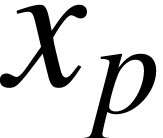 and
and 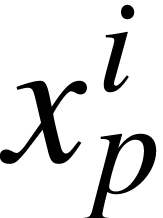 are close (like in
are close (like in 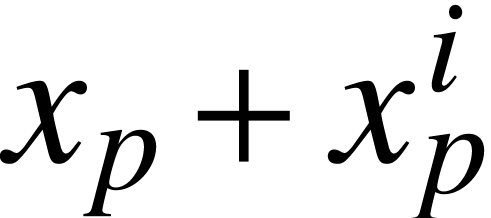 ),
then it is natural to opt for a common base line. However, if they are
further away from each other (like in
),
then it is natural to opt for a common base line. However, if they are
further away from each other (like in  ),
then we might want to opt for different base lines and locally optimize
the rendering of the first
),
then we might want to opt for different base lines and locally optimize
the rendering of the first 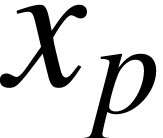 .
.
Consequently, TeXmacs should offer a reasonable compromise for the most
frequent cases, while offering methods for the user to make finer
adjustments in the remaining ones. We provide the constructs →→ and →→ to move and resize boxes in order to perform such adjustments.
For instance, if the brackets around the two sums
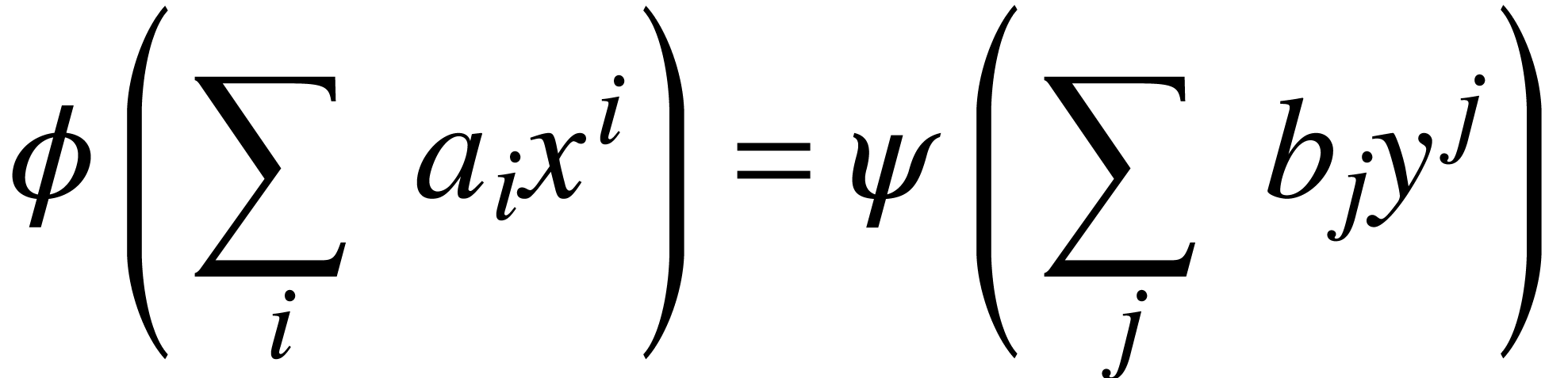
have different sizes, then one may resize the bottom of the subscript
 of the second sum to 0fn.
Alternatively, one may resize the bottoms of both the
of the second sum to 0fn.
Alternatively, one may resize the bottoms of both the  and
and  subscripts to (say) -0.3fn.
For easier adjustments you may use →→ and →→
to automatically adjust the size of the contents to the height of the
character “x” and the largest one in the font respectively.
subscripts to (say) -0.3fn.
For easier adjustments you may use →→ and →→
to automatically adjust the size of the contents to the height of the
character “x” and the largest one in the font respectively.
Notice that one should adjust by preference in a structural and not
visual way. For instance, one should prefer -0.3fn to
-2mm in the above example, because the second option
disallows you to switch to another font size for your document.
Similarly, you should try not change the semantics of the formula. For
instance, in the above example, you might have added a “dummy
subscript” to the  subscript of the sum.
However, this would alter the meaning of the formula (whence make it non
suitable as input to a computer algebra system) In the future, we plan
to provide additional constructs in order to facilitate structural
adjusting. For instance, in the case of a formula like
subscript of the sum.
However, this would alter the meaning of the formula (whence make it non
suitable as input to a computer algebra system) In the future, we plan
to provide additional constructs in order to facilitate structural
adjusting. For instance, in the case of a formula like
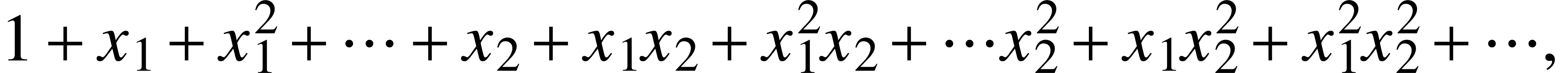
one might think of a construct to enclose the entire formula into an
area, where all scripts are forced to be double (using dummy
superscripts wherever necessary).
2.Mathematical primitives
<left|large-delimiter>
<left|large-delimiter|size>
<left|large-delimiter|bottom|top>
<mid|large-delimiter| >
>
<right|large-delimiter| >
>
(large delimiters)
These primitives are used for producing large delimiters, like in the
formula
Matching left and right delimiters are automatically sized so as
contain the enclosed expression. Between matching left and right
delimiters, the formula may contain an arbitrary number of middle
delimiters, which are sized in a similar way. Contrary to TeX, the
depth of a large delimiter is not necessarily equal to its height, so
as to correctly render formulas like
The user may override the automatically determined size by specifying
additional length parameters size or bottom and top. For
instance,
f<left|(|-8mm|4mm>x<mid|||8mm>y<right|)|-4mm|8mm>
is rendered as
The size may also be a number 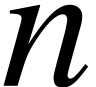 , in which case the
, in which case the 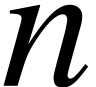 -th available size for the delimiter is taken. For
instance,
-th available size for the delimiter is taken. For
instance,
g<left|(|0><left|(|1><left|(|2><left|(|3>z<right|)|3><right|)|2><right|)|1><right|)|0>
is rendered as
<big|big-symbol>
(big symbols)
This primitive is used in order to produce big operators as in
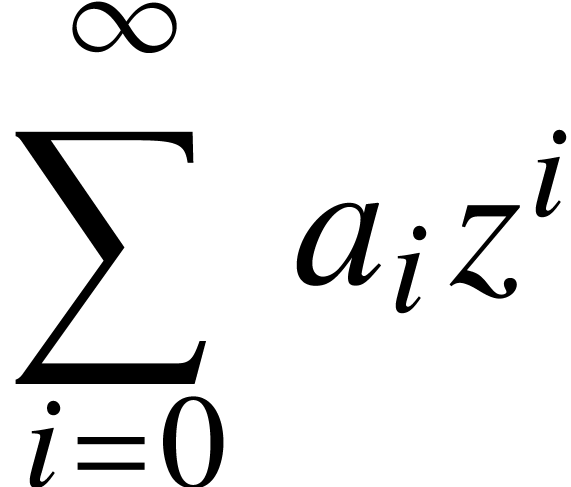 |
(1) |
The size of the operator depends on whether the formula is rendered in
“display style” or not. Formulas in separate equations,
like (1), are said to be rendered in display style,
contrary to formulas which occur in the main text, like 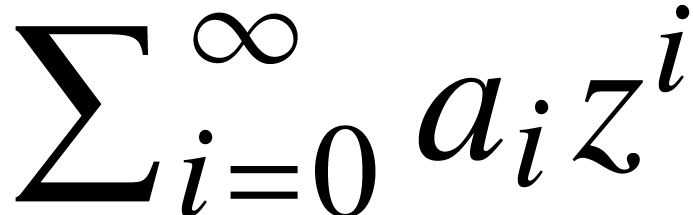 . The user may use → to override the current
settings.
. The user may use → to override the current
settings.
Notice that the formula (1) is internally represented as
<big|sum><rsub|i=0><rsup|∞>a<rsub|i>*z<rsup|i><big|.>
The invisible big operator <big|.> is used to indicate the end of
the scope of <big|sum>.
<frac|num|den>
(fractions)
The frac primitive is used in order to render
fractions like  . In display
style, the numerator num and denominator
den are rendered in the normal size, but
display style is turned of when typesetting num
and den. When the display style is turned
of, then the arguments are rendered in script size. For instance, the
content
. In display
style, the numerator num and denominator
den are rendered in the normal size, but
display style is turned of when typesetting num
and den. When the display style is turned
of, then the arguments are rendered in script size. For instance, the
content
<frac|1|a<rsub|0>+<frac|1|a<rsub|1>+<frac|1|a<rsub|2>+⋱>>>
is rendered in display style as
<sqrt|content>
<sqrt|content|n>
(roots)
The sqrt primitive is used in order to render
square roots like 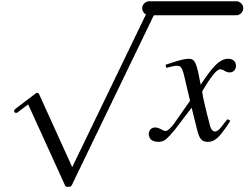 or n-th
roots like
or n-th
roots like 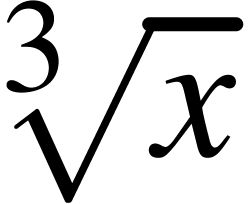 . The root
symbol is automatically sized so as to encapsulate the content:
. The root
symbol is automatically sized so as to encapsulate the content:
<lsub|script>
<lsup|script>
<rsub|script>
<rsup|script>
(scripts)
These primitives are used in order to attach a script
to the preceding box in a horizontal concatenation (in the case of
right scripts) or the next one (in the case of left scripts). When
there is no such box, then the script is attached to an empty box.
Moreover, when both a subscript and a superscript are specified on the
same side, then they are merged together. For instance, the expression
<rsub|a><rsup|b>+<lsub|1><lsup|2>x<rsub|3><rsup|4>=y<rsub|1>+<lsub|c>
is rendered as
When a right script is attached to an operator (or symbol) which
accepts limits, then it is rendered below or above instead of beside
the operator:
Scripts are rendered in a smaller font in non-display style.
Nevertheless, in order to keep formulas readable, the size is not
reduced below script-script-size.
<lprime|prime-symbols>
<rprime|prime-symbols>
(primes)
Left and right primes are similar to left and right superscripts,
except that they behave in a different way when being edited. For
instance, when your cursor is behind the prime symbol in 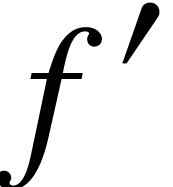 and you press backspace, then the prime is removed. If
you are behind
and you press backspace, then the prime is removed. If
you are behind 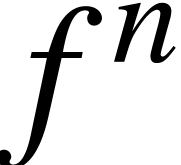 and you press backspace several
times, then you first enter the superscript, next remove
and you press backspace several
times, then you first enter the superscript, next remove 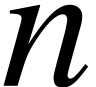 and finally remove the superscript. Notice also that
prime-symbols is necessarily a string of
concatenated prime symbols. For instance,
and finally remove the superscript. Notice also that
prime-symbols is necessarily a string of
concatenated prime symbols. For instance, 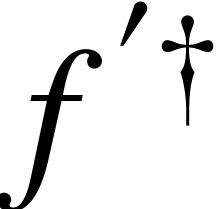 is
represented by f<rprime|'†>.
is
represented by f<rprime|'†>.
<below|content|script>
<above|content|script>
(scripts above and below)
The below and above tags are
used to explicitly attach a script below or
above a given content. Both can be mixed in
order to produce content with both a script below and above:
can be produced using
<above|<below|xor|i=1>|∞> x<rsub|i>
<wide|content|wide-symbol>
<wide*|content|wide-symbol>
(wide symbols)
These primitives can be used in order to produce wide accents above or
below some mathematical content. For
instance  corresponds to the markup <wide|x+y|¯>.
corresponds to the markup <wide|x+y|¯>.
<neg|content>
(negations)
This primitive is mainly used for producing negated symbols or
expressions, such as 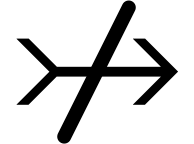 or
or  .
.
<tree|root|child-1| |child-n>
|child-n>
(trees)
This primitive is used to produce a tree with a given root
and children child-1 until child-n.
The primitive should be used recursively in order to produce trees.
For instance,
corresponds to the markup
<tree|+|x|y|<tree|×|2|y|z>>
In the future, we plan to provide further style parameters in order to
control the rendering.
3.The font parameters
Several font parameters are crucial for the correct positioning of the
different components. The following are often needed:
quad
The main font reference space 1fn, which can be
taken as the distance between successive lines of text.
y1 and y2
The bottom and top level for the font (we have y2-y1=quad).
sep
The reference minimal space between distinct components, like the
minimal distance between a subscript and a superscript. In fact,
sep=quad/10.
wline
The width of several types of lines, like the fraction and square
root bars, wide accents, etc.
yfrac
The height of the fraction bar, which is needed for the
positioning of fractions and big delimiters. Usually, yfrac
is almost equal to yx/2 below.
The following parameters are mainly needed in order to deal with
scripts:
yx
The height of the  character, which is
needed for the positioning of scripts. All the remaining
parameters are actually computed as a function of yx.
character, which is
needed for the positioning of scripts. All the remaining
parameters are actually computed as a function of yx.
ysub lo base
Logical base line for subscripts.
ysub hi lim
Subscripts may never physically exceed this top height.
ysup lo base
Logical base line for superscripts.
ysup lo lim
Superscripts may never physically exceed this bottom height.
ysup hi lim
Suggestion for a physical top line for superscripts.
yshift
Possible shift of the base lines when we are inside fractions or
scripts.
The individual strings in a font also have several important positioning
properties. First of all, they always admit left and right slopes.
Furthermore, they admit left and right italic corrections, which are
needed for the positioning of scripts or when passing from text in
upright to text in italics (or vice versa).
4.Implementation of the mathematical
primitives
The typesetting semantics of TeXmacs documents is implemented by
void concater_rep::typeset (tree t, path ip);
in src/Typeset/Concat/concat_math.cpp which dispatch
according to the current tree label to more specialized routines, which
we will describe below.
Tree labels for mathematical typesettings are (in scr/Kernel/Types/tree_label.hpp)
enum tree_label {
// [… other labels …]
// mathematics
AROUND, VAR_AROUND, BIG_AROUND,
LEFT, MID, RIGHT, BIG, LONG_ARROW,
LPRIME, RPRIME, BELOW, ABOVE,
LSUB, LSUP, RSUB, RSUP,
FRAC, SQRT, WIDE, VAR_WIDE, NEG, TREE,
SYNTAX,
// [… other labels …]
};
They provide labels for the primitives to typeset brackets (around,
var_around, big_around, left, mid, right),
sub/super-scripts (lsup, lsub, rsup, rsub), accents (lprime,
rprime), above and below formulas (below,
above) fractions (frac), roots (sqrt), wide under and over braces (wide, var_wide), negations (neg), and trees (tree) or syntax (syntax) constructions.
4.1.Primed expressions
Primed expressions are encoded in TeXmacs as

|
<math|a<rprime|'>,a<rprime|‡>,<lprime|‡>s>
|
and are typeset via the following code (the code for rprime
is analogous and is not shown):
void
concater_rep::typeset_lprime (tree t, path ip) {
if ((N(t) == 1) && is_atomic (t[0])) {
string s= t[0]->label;
bool flag= (env->fn->type == FONT_TYPE_UNICODE);
if (flag)
for (int i=0; i<N(s); i++)
flag= flag && (s[i] == '\'' || s[i] == '‘');
if (env->fn->type == FONT_TYPE_TEX ||
env->fn->math_type != MATH_TYPE_NORMAL)
s= replace_primes (s);
tree old_il;
if (!flag) old_il= env->local_begin_script ();
path sip= descend (ip, 0);
box b1, b2;
b2= typeset_as_concat (env, s /*t[0]*/, sip);
b2= symbol_box (sip, b2, N(t[0]->label));
if (flag || env->fn->math_type != MATH_TYPE_TEX_GYRE)
b2= move_box (sip, b2,
flag? 0: env->as_length (string ("-0.05fn")),
flag? env->as_length ("-0.75ex"): 0,
false, true);
if (!flag) env->local_end_script (old_il);
print (LSUP_ITEM, OP_SKIP, script_box (ip, b1, b2, env->fn));
penalty_max (HYPH_INVALID);
}
else typeset_error (t, ip);
}
Note that we output an LSUP_ITEM, since later on, in a
second pass, we need to reposition these boxes as we will do for sub,
superscripts.
The replace_primes function:
string
replace_primes (string s) {
string r;
int i, n= N(s);
for (i=0; i<n; i++)
if (s[i] == '\'') r << "<prime>";
else if (s[i] == '‘') r << "<backprime>";
else r << s[i];
return r;
}
4.2.Fractions
Fractions can be inline 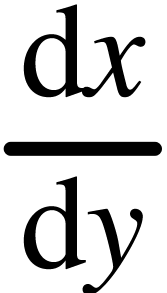 or in display style and
have different variants (standard frac, display dfrac, small inline tfrac, continued cfrac and slashed frac*). For example
or in display style and
have different variants (standard frac, display dfrac, small inline tfrac, continued cfrac and slashed frac*). For example
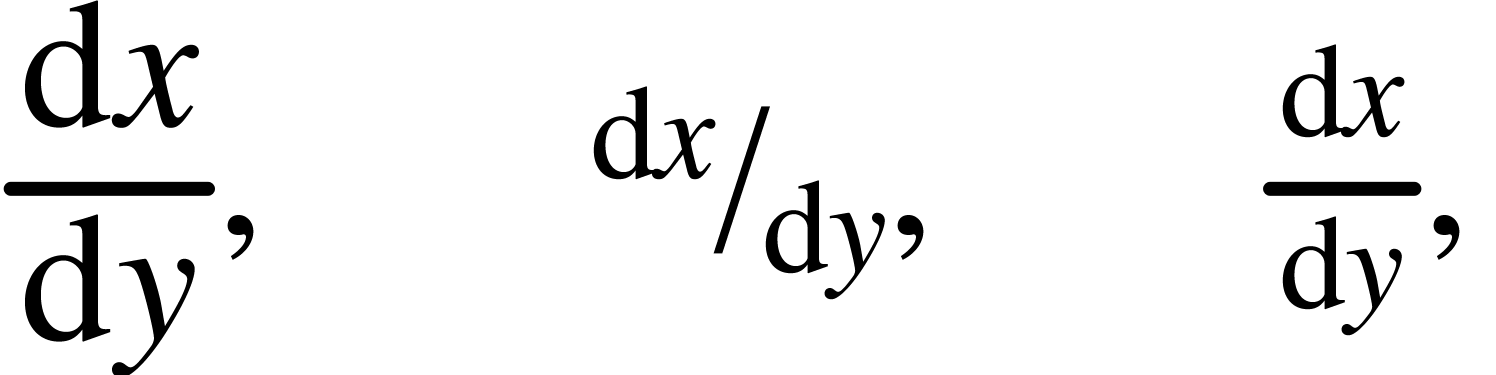
|
<dfrac|\<mathd\>x|\<mathd\>y>,<space|2em>
<frac*|\<mathd\>x|\<mathd\>y>,
<math|<dfrac|dx|dy>,<space|2em><frac*|dx|dy>,<space|2em><tfrac|dx|dy>,>
|
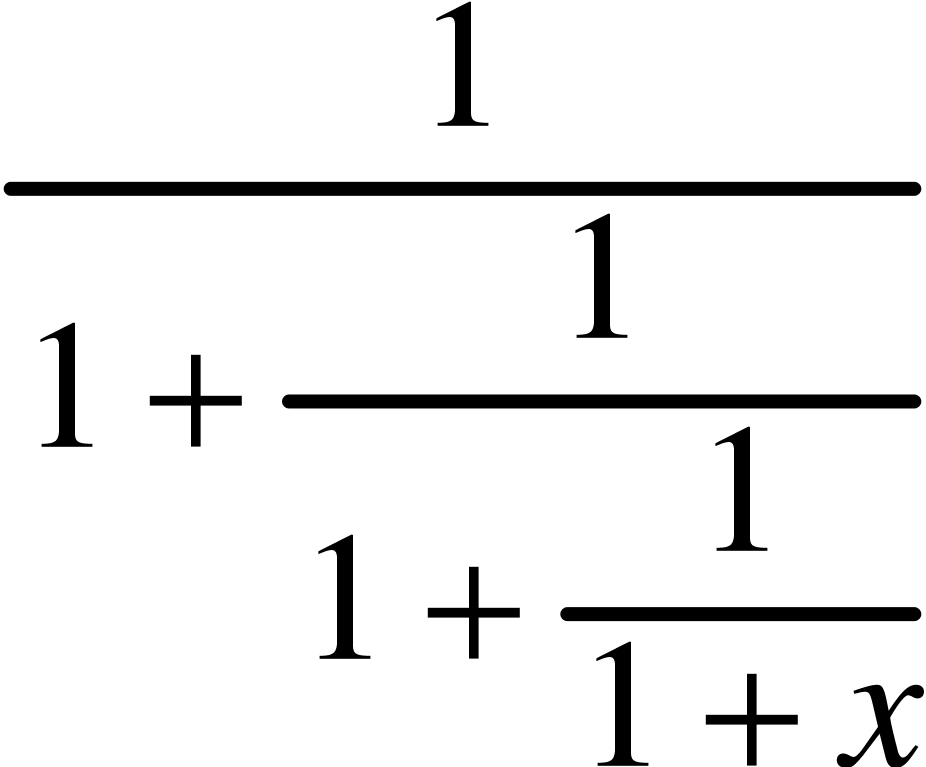
|
<cfrac|1|1+<cfrac|1|1+<cfrac|1|1+x>>>
|
Apart from frac, the others tags are implemented in std-maths.ts as:
<document|<assign|tfrac|<macro|x|y|<with|mode|math|<with|math-display|false|<frac|x|y>>>>>||<assign|dfrac|<macro|x|y|<with|mode|math|<with|math-display|true|<frac|x|y>>>>>||<assign|cfrac|<macro|x|y|<with|mode|math|<dfrac|x|<resize|y|||<plus|1r|-1sep>|>>>>>||<assign|frac*|<macro|x|y|<move|<lsup|x><resize|/|<plus|1l|0.15em>|<plus|1b|0.5em>|<minus|1r|0.15em>|<minus|1t|0.5em>><rsub|y>||0.05em>>>||<drd-props|frac*|arity|2|syntax|<macro|x|y|x/y>>>
The frac tag is primitive and typesetted by concater_rep::typeset_frac
:
void
concater_rep::typeset_frac (tree t, path ip) {
if (N(t) != 2) { typeset_error (t, ip); return; }
bool disp= env->display_style;
tree old;
if (disp) old= env->local_begin (MATH_DISPLAY, "false");
else old= env->local_begin_script ();
tree old_vp= env->local_begin (MATH_VPOS, "1");
box num= typeset_as_concat (env, t[0], descend (ip, 0));
env->local_end (MATH_VPOS, "-1");
box den= typeset_as_concat (env, t[1], descend (ip, 1));
env->local_end (MATH_VPOS, old_vp);
font sfn= env->fn;
if (disp) env->local_end (MATH_DISPLAY, old);
else env->local_end_script (old);
if (num->w() <= env->frac_max && den->w () <= env->frac_max)
print (frac_box (ip, num, den, env->fn, sfn, env->pen));
else typeset_wide_frac (t, ip);
}
The "math-vpos" environment variable is set to
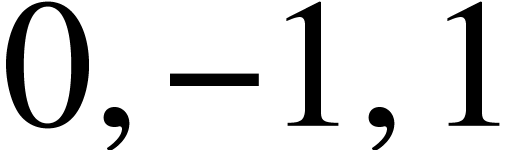 depending on where we are in the typesetting of
fractions. This is used in the finalization routines. [Add
more?]
depending on where we are in the typesetting of
fractions. This is used in the finalization routines. [Add
more?]
The function frac_box inserts an instance of frac_box_rep
frac_box_rep::frac_box_rep (
path ip, box b1, box b2, font fn2, font sfn2, pencil pen2):
composite_box_rep (ip), fn (fn2), sfn (sfn2), pen (pen2)
{
// Italic correction does not lead to nicer results,
// because right correction is not equilibrated w.r.t. left correction
SI bar_y = fn->yfrac;
SI bar_w = fn->wline;
SI sep = fn->sep;
SI b1_y = min (b1->y1, sfn->y1);
SI b2_y = max (b2->y2, sfn->y2);
SI w = max (b1->w (), b2->w()) + 2*sep;
SI d = sep >> 1;
pencil bar_pen= pen->set_width (bar_w);
insert (b1, (w>>1) - (b1->x2>>1), bar_y+ sep+ (bar_w>>1)- b1_y);
insert (b2, (w>>1) - (b2->x2>>1), bar_y- sep- (bar_w>>1)- b2_y);
insert (line_box (decorate_middle (ip), d, 0, w-d, 0, bar_pen), 0, bar_y);
italic_correct (b1);
italic_correct (b2);
position ();
italic_restore (b1);
italic_restore (b2);
x1= min (0, x1);
x2= max (w, x2);
left_justify ();
finalize ();
}
The following heuristics are used:
-
The horizontal middles of the numerator and the denominator are
taken to be the same.
-
The vertical spaces between the numerator resp.
denominator and the fraction bar is at least sep.
-
The depth (resp. height) of the numerator
(resp. denominator) is descended (resp.
increased) to y1 (resp. y2)
if necessary. This forces the base lines of not too large numerators
resp. denominators to be the same in presence of
multiple fractions.
-
The fraction bar has a overhang of sep/2 to both
sides and the logical limits of the fraction are another sep/2
further. The logical left limit is zero.
The italic corrections are not taken into account during the positioning
algorithms, because this may create the impression that the numerator
and denominator are not correctly centered with respect to each other.
Nevertheless, the italic corrections are taken into account in order to
compute the logical bounding box of the fraction (whose has italic
slopes vanish at both sides).
In the case the fraction's numerator or denominator are very wide a
fallback typesetting strategy is used, according to:
void
concater_rep::typeset_wide_frac (tree t, path ip) {
bool numb= needs_brackets (t[0], "Product");
bool denb= needs_brackets (t[1], "Power");
pencil old_pen= env->pen;
marker (descend (ip, 0));
typeset_large (tree (LEFT, "."), decorate_left (descend (ip, 0)),
LEFT_BRACKET_ITEM, OP_OPENING_BRACKET, "<left-");
env->pen= env->flatten_pen;
if (numb)
typeset_large (tree (LEFT, "("), decorate_left (descend (ip, 0)),
LEFT_BRACKET_ITEM, OP_OPENING_BRACKET, "<left-");
env->pen= old_pen;
typeset (t[0], descend (ip, 0));
env->pen= env->flatten_pen;
if (numb)
typeset_large (tree (RIGHT, ")"), decorate_right (descend (ip, 0)),
RIGHT_BRACKET_ITEM, OP_CLOSING_BRACKET, "<right-");
typeset_large (tree (MID, "/"), decorate_middle (ip),
MIDDLE_BRACKET_ITEM, OP_MIDDLE_BRACKET, "<mid-");
if (denb)
typeset_large (tree (LEFT, "("), decorate_left (descend (ip, 1)),
LEFT_BRACKET_ITEM, OP_OPENING_BRACKET, "<left-");
env->pen= old_pen;
typeset (t[1], descend (ip, 1));
env->pen= env->flatten_pen;
if (denb)
typeset_large (tree (RIGHT, ")"), decorate_right (descend (ip, 1)),
RIGHT_BRACKET_ITEM, OP_CLOSING_BRACKET, "<right-");
env->pen= old_pen;
typeset_large (tree (RIGHT, "."), decorate_right (descend (ip, 1)),
RIGHT_BRACKET_ITEM, OP_CLOSING_BRACKET, "<right-");
marker (descend (ip, 1));
}
4.3.Roots
The following heuristics are used:
-
The vertical space between the main argument and the upper bar is at
least sep.
-
The root itself is typeset like a large delimiter. The positioning
of a potential script is very dependent on the usage of TeX fonts.
[make precise]
-
The upper bar has a overhang of sep/2 at the right
and the logical right limit of the root is situated another sep/2 further to the right.
We take the logical right border plus the italic correction of the main
argument in order to determine the right hand limit of the upper bar.
The left italic correction is not needed.
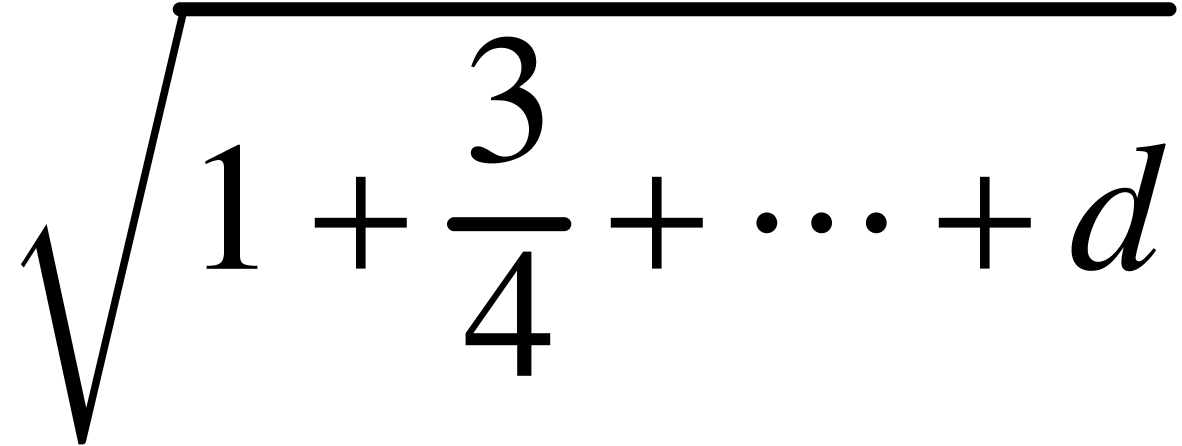
|
<sqrt|1+<frac|3|4>+\<cdots\>+d>
|
Typesetting goes as follows:
void
concater_rep::typeset_sqrt (tree t, path ip) {
if (N(t) != 1 && N(t) != 2) { typeset_error (t, ip); return; }
box b= typeset_as_concat (env, t[0], descend (ip, 0));
if (b->w () > env->frac_max) { typeset_wide_sqrt (t, ip); return; }
box ind;
if (N(t)==2) {
bool disp= env->display_style;
tree old;
if (disp) old= env->local_begin (MATH_DISPLAY, "false");
tree old_il= env->local_begin_script ();
ind= typeset_as_concat (env, t[1], descend (ip, 1));
env->local_end_script (old_il);
if (disp) env->local_end (MATH_DISPLAY, old);
}
SI sep= env->fn->sep;
font lfn= env->fn;
bool stix= starts (lfn->res_name, "stix-");
if (stix) lfn= rubber_font (lfn);
box sqrtb= delimiter_box (decorate_left (ip), "<large-sqrt>",
lfn, env->pen, b->y1, b->y2 + (3*sep >> 1));
if (stix) sqrtb= shift_box (decorate_left (ip), sqrtb,
-env->fn->wline/2, -env->fn->wline/3,
false, true);
print (sqrt_box (ip, b, ind, sqrtb, env->fn, env->pen));
}
sqrt_box_rep::sqrt_box_rep (
path ip, box b1, box b2, box sqrtb, font fn2, pencil pen2):
composite_box_rep (ip), fn (fn2), pen (pen2)
{
right_italic_correct (b1);
SI sep = fn->sep;
SI wline= fn->wline;
SI dx = -fn->wfn/36, dy= -fn->wfn/36; // correction
SI by = sqrtb->y2+ dy;
if (sqrtb->x2 - sqrtb->x4 > wline) dx -= (sqrtb->x2 - sqrtb->x4);
pencil rpen= pen->set_width (wline);
insert (b1, 0, 0);
if (!is_nil (b2)) {
SI X = - sqrtb->w();
SI M = X / 3;
SI Y = sqrtb->y1;
SI bw= sqrtb->w();
SI bh= sqrtb->h();
if (fn->math_type == MATH_TYPE_TEX_GYRE) {
if (2*bh < 9*bw) Y += bh >> 1;
else if (occurs ("ermes", fn->res_name)) Y += (19*bw) >> 3;
else if (occurs ("agella", fn->res_name)) Y += (16*bw) >> 3;
else Y += (15*bw) >> 3;
}
else {
if (bh < 3*bw) Y += bh >> 1;
else Y += (bw*3) >> 1;
}
insert (b2, min (X, M- b2->x2), Y- b2->y1+ sep);
}
insert (sqrtb, -sqrtb->x2, 0);
insert (line_box (decorate_middle (ip), dx, by, b1->x2, by, rpen), 0, 0);
position ();
left_justify ();
y1 -= wline;
y2 += wline;
x2 += sep >> 1;
right_italic_restore (b1);
finalize ();
}
Wide versions of the square root goes as follows:
void
concater_rep::typeset_wide_sqrt (tree t, path ip) {
bool br= needs_brackets (t[0], "Postfixed");
pencil old_pen= env->pen;
marker (descend (ip, 0));
typeset_large (tree (LEFT, "."), decorate_left (descend (ip, 0)),
LEFT_BRACKET_ITEM, OP_OPENING_BRACKET, "<left-");
env->pen= env->flatten_pen;
if (br)
typeset_large (tree (LEFT, "("), decorate_left (descend (ip, 0)),
LEFT_BRACKET_ITEM, OP_OPENING_BRACKET, "<left-");
env->pen= old_pen;
typeset (t[0], descend (ip, 0));
env->pen= env->flatten_pen;
if (br)
typeset_large (tree (RIGHT, ")"), decorate_right (descend (ip, 0)),
RIGHT_BRACKET_ITEM, OP_CLOSING_BRACKET, "<right-");
env->pen= old_pen;
bool disp= env->display_style;
tree old;
if (disp) old= env->local_begin (MATH_DISPLAY, "false");
tree old_il= env->local_begin_script ();
env->pen= env->flatten_pen;
box num= typeset_as_concat (env, "1", decorate_middle (ip));
box den;
if (N(t) >= 2) {
env->pen= old_pen;
den= typeset_as_concat (env, t[1], descend (ip, 1));
env->pen= env->flatten_pen;
}
else den= typeset_as_concat (env, "2", decorate_middle (ip));
box fr= frac_box (decorate_middle (ip), num, den, env->fn, env->fn, env->pen);
env->pen= old_pen;
env->local_end_script (old_il);
if (disp) env->local_end (MATH_DISPLAY, old);
penalty_max (HYPH_INVALID);
a << line_item (RSUP_ITEM, OP_SKIP,
script_box (ip, box (), fr, env->fn), HYPH_INVALID);
typeset_large (tree (RIGHT, "."), decorate_right (descend (ip, 1)),
RIGHT_BRACKET_ITEM, OP_CLOSING_BRACKET, "<right-");
marker (descend (ip, 1));
}
4.4.Negations
Negations are barred expressions:
The following heuristics are used:
-
The negation bar passes through the logical center of the argument.
-
The italic corrections of the argument are only taken into account
during the computation of the logical limits of the negation box
(which has zero left and right slopes).
Typesetting of negation tags is very elementary
void
concater_rep::typeset_neg (tree t, path ip) {
if (N(t) != 1) { typeset_error (t, ip); return; }
box b= typeset_as_concat (env, t[0], descend (ip, 0));
print_semantic (neg_box (ip, b, env->fn, env->pen), t[0]);
}
and give rise to negation boxes:
neg_box_rep::neg_box_rep (path ip, box b, font fn2, pencil pen2):
composite_box_rep (ip), fn (fn2), pen (pen2)
{
SI wline= fn->wline;
SI delta= fn->wfn/6;
SI X = (b->x1 + b->x2) >> 1;
SI Y = (b->y1 + b->y2) >> 1;
SI DX, DY;
pencil npen= pen->set_width (wline);
insert (b, 0, 0);
if ((3*(b->x2-b->x1)) > (2*(b->y2-b->y1))) {
DY= delta + ((b->y2 - b->y1)>>1);
DX= DY>>1;
}
else {
DX= delta + ((b->x2 - b->x1)>>1);
DY= DX;
}
insert (line_box (decorate_middle (ip), X+DX, Y+DY, X-DX, Y-DY, npen), 0, 0);
italic_correct (b);
position ();
italic_restore (b);
finalize ();
}
4.5.Wide boxes
Wide boxes are used for under and over-braces and wide accents:
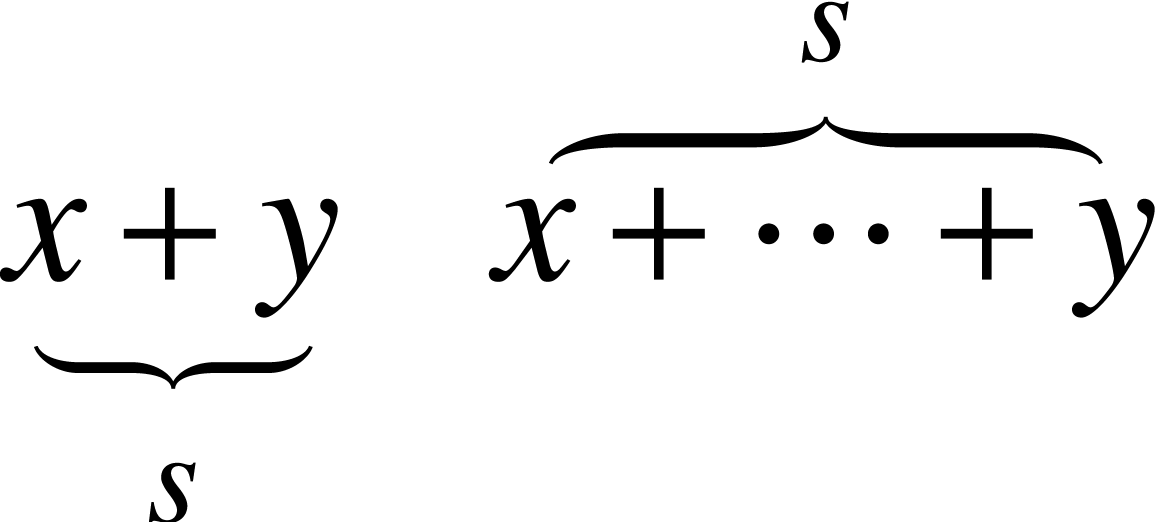
|
<wide*|x+y|\<wide-underbrace\>><rsub|s>
<wide|x+\<cdots\>+y|\<wide-overbrace\>><rsup|s>
|
The following heuristics are used:
-
We use TeX fonts for small accents and an ad hoc algorithm
for the wider ones.
-
The distance between the main argument and the accent is at least
sep (or a distance which depends on the TeX font for
small accents).
-
The accent is positioned horizontally according to the right slope
of the main argument.
-
The slopes for the accented box are inherited from those of the main
argument and the italic corrections are adjusted accordingly.
-
All script height parameters of the accented box are inherited from
the main argument. The only exception is ysup_hi_lim,
which may be increased by the height of the accent, or determined in
the generic way, whichever leads to the least value. It is indeed
better to keep superscripts positioned reasonably low, whenever
possible.
void
concater_rep::typeset_wide (tree t, path ip, bool above) {
if (N(t) != 2) { typeset_error (t, ip); return; }
box b= typeset_as_concat (env, t[0], descend (ip, 0));
string s= env->exec_string (t[1]);
if (s == "^") s= "<hat>";
if (s == "~") s= "<tilde>";
bool request_wide= false;
if (starts (s, "<wide-")) {
s= "<" * s (6, N(s));
request_wide= true;
}
if (ends (s, "brace>") || ends (s, "brace*>"))
b= move_box (decorate_middle (descend (ip, 0)), b, 0, 0, true);
box wb= wide_box (ip, b, s, env->fn, env->pen, request_wide, above);
print_semantic (wb, t[0]);
if (ends (s, "brace>")) with_limits (LIMITS_ALWAYS);
}
wide_box produces a wide_box_rep whose
constructor perform further computations and handling of special cases:
wide_box_rep::wide_box_rep (
path ip, box ref2, string s2, font fn2, pencil pen2,
bool request_wide2, bool above2):
composite_box_rep (ip), ref (ref2), s (s2), fn (fn2), pen (pen2),
request_wide (request_wide2), above (above2)
{
box hi;
wide= compute_wide_accent (ip, ref, s, fn, pen, request_wide, above, hi, sep);
SI X, Y, dx;
SI hw= max (ref->w(), hi->w()) >> 1;
SI m = (ref->x1 + ref->x2) >> 1;
insert (ref, 0, 0);
if (above) {
Y= ref->y2;
X= m;
if (ref->right_slope () != 0)
X += ref->rsup_correction() + ((SI) (ref->right_slope() * fn->yx * 0.5));
X += ref->wide_correction (1);
//X= ((SI) (ref->right_slope () * (Y - fn->yx))) + m;
insert (hi, X- ((hi->x1 + hi->x2)>>1), Y+ sep);
}
else {
Y= ref->y1 - hi->y2;
X= m - ((SI) (ref->right_slope () * sep));
X += ref->wide_correction (-1);
//X= ((SI) (ref->right_slope () * (Y - sep))) + m;
insert (hi, X- ((hi->x1 + hi->x2)>>1), Y- sep);
}
position ();
dx= x1;
left_justify ();
dh= hi->y2+ sep;
dw= (SI) (dh * ref->right_slope ());
dd= fn->sep;
x1= m- hw- dx;
x2= m+ hw- dx;
x1= min (x1, ref->x1);
x2= max (x2, ref->x2);
if (!above) y1 += fn->sep - sep;
finalize ();
}
The computation of the wide accent is more involved and divided in
several cases.
bool
compute_wide_accent (path ip, box b, string s,
font fn, pencil pen, bool request_wide, bool above,
box& wideb, SI& sep) {
bool unicode= (fn->type == FONT_TYPE_UNICODE);
bool stix= (fn->math_type == MATH_TYPE_STIX);
bool tex_gyre= (fn->math_type == MATH_TYPE_TEX_GYRE);
bool wide= (b->w() > (fn->wquad)) || request_wide;
if (ends (s, "dot>") || (s == "<acute>") ||
(s == "<grave>") || (s == "<abovering>")) wide= false;
if (wide && !request_wide && b->wide_correction (0) != 0) wide= false;
bool very_wide= false;
SI accw= fn->wfn;
if (wide) {
if (tex_gyre) {
if (s == "^" || s == "<hat>" ||
s == "~" || s == "<tilde>" ||
s == "<check>")
very_wide= (b->w() >= ((8*fn->wfn) >> 2));
else if (ends (s, "brace>") || ends (s, "brace*>")) {
if (starts (s, "<sq"))
very_wide= (b->w() >= ((11*fn->wfn) >> 2));
else very_wide= (b->w() >= ((15*fn->wfn) >> 2));
}
else very_wide= true;
}
else if (!unicode) {
if (s == "^" || s == "<hat>" || s == "~" || s == "<tilde>")
very_wide= (b->w() >= ((9*fn->wfn) >> 2));
else very_wide= true;
}
else if (stix) very_wide= true;
/*
else if (s == "^" || s == "<hat>" || s == "~" || s == "<tilde>" ||
s == "<bar>" || s == "<vect>" || s == "<check>" ||
s == "<breve>" || s == "<invbreve>") {
box wb= text_box (decorate_middle (ip), 0, s, fn, pen);
accw= wb->x4 - wb->x3;
if (b->w() >= 16*accw) very_wide= true;
}
*/
else very_wide= true;
}
if (wide && stix) {
if (s == "^") s= "<hat>";
if (s == "~") s= "<tilde>";
if (s == "<hat>" || s == "<tilde>" || s == "<check>" ||
ends (s, "brace>") || ends (s, "brace*>")) {
font rfn= rubber_font (fn);
SI width= b->x2- b->x1 - fn->wfn/4;
wideb= wide_stix_box (decorate_middle (ip),
"<rubber-" * s (1, N(s)-1) * ">",
rfn, pen, width);
if (wideb->w() >= width) {
if (b->right_slope () != 0)
wideb= shift_box (decorate_middle (ip), wideb,
(SI) (-0.5 * b->right_slope () * fn->yx), 0);
sep= above? -fn->yx: fn->sep;
if (above) {
if (s == "<overbrace>" || s == "<squnderbrace*>") sep= 2 * fn->sep;
if (s == "<poverbrace>") sep= 3 * fn->sep;
}
return wide;
}
}
}
if (very_wide) {
SI w= fn->wline;
if (stix) w= (SI) (1.189 * w);
pencil wpen= pen->set_width (w);
if ((s == "^") || (s == "<hat>"))
wideb= wide_hat_box (decorate_middle (ip), b->x1, b->x2, wpen);
else if ((s == "~") || (s == "<tilde>"))
wideb= wide_tilda_box (decorate_middle (ip), b->x1, b->x2, wpen);
else if (s == "<bar>")
wideb= wide_bar_box (decorate_middle (ip), b->x1, b->x2, wpen);
else if (s == "<vect>")
wideb= wide_vect_box (decorate_middle (ip), b->x1, b->x2, wpen);
else if (s == "<check>")
wideb= wide_check_box (decorate_middle (ip), b->x1, b->x2, wpen);
else if (s == "<breve>" || s == "<punderbrace>" || s == "<punderbrace*>")
wideb= wide_breve_box (decorate_middle (ip), b->x1, b->x2, wpen);
else if (s == "<invbreve>" || s == "<poverbrace>" || s == "<poverbrace*>")
wideb= wide_invbreve_box(decorate_middle (ip), b->x1, b->x2, wpen);
else if (s == "<squnderbrace>" || s == "<squnderbrace*>")
wideb= wide_squbr_box (decorate_middle (ip), b->x1, b->x2, wpen);
else if (s == "<sqoverbrace>" || s == "<sqoverbrace*>")
wideb= wide_sqobr_box (decorate_middle (ip), b->x1, b->x2, wpen);
else wideb= wide_box (decorate_middle (ip),
"<rubber-" * s (1, N(s)-1) * ">",
fn, pen, b->x2- b->x1);
sep= fn->sep;
if (stix || !unicode) sep= (SI) (1.5 * sep);
}
else if (wide && tex_gyre) {
string ws= "<wide-" * s (1, N(s)-1) * ">";
SI width= b->x2- b->x1 - fn->wfn/4;
wideb= wide_box (decorate_middle (ip), ws, fn, pen, width);
if (b->right_slope () != 0) {
bool times= stix || (tex_gyre && occurs ("ermes", fn->res_name));
double factor= ((times || !above)? 0.2: 0.5);
wideb= shift_box (decorate_middle (ip), wideb,
(SI) (-factor * b->right_slope () * fn->yx), 0);
}
sep= above? -fn->yx: fn->sep;
}
else if (wide && !unicode) {
string ss= s (1, N(s)-1);
if (ss == "^") ss= "hat";
if (ss == "~") ss= "tilde";
string ws= "<wide-" * ss * ">";
SI width= b->x2- b->x1 - fn->wfn/4;
wideb= wide_box (decorate_middle (ip), ws, fn, pen, width);
if (b->right_slope () != 0) {
double factor= (above? 0.5: 0.2);
wideb= shift_box (decorate_middle (ip), wideb,
(SI) (-factor * b->right_slope () * fn->yx), 0);
}
sep= above? -fn->yx: fn->sep;
}
else if (wide) {
SI pad= fn->wfn - accw;
pad= (SI) ((0.75 * accw * pad) / (b->w() - pad));
double sx= ((double) (b->w() - pad)) / ((double) accw);
sx= floor (4.0*sx) / 4.0;
double sy= sqrt (sqrt (sx));
font sfn= fn->magnify (sx, sy);
wideb= text_box (decorate_middle (ip), 0, s, sfn, pen);
wideb= resize_box (decorate_middle (ip), wideb,
max (wideb->x1, wideb->x3), wideb->y1,
min (wideb->x2, wideb->x4), wideb->y2);
if (unicode && b->right_slope () != 0)
wideb= shift_box (decorate_middle (ip), wideb,
(SI) (-0.5 * b->right_slope () * fn->yx), 0);
sep= above? -fn->yx: fn->sep;
if (above) sep -= 3 * (sy - 1.0) * fn->sep;
}
else {
wideb= text_box (decorate_middle (ip), 0, s, fn, pen);
if (unicode && b->right_slope () != 0) {
bool times= stix || (tex_gyre && occurs ("ermes", fn->res_name));
double factor= ((times || !above)? 0.2: 0.5);
wideb= shift_box (decorate_middle (ip), wideb,
(SI) (-factor * b->right_slope () * fn->yx), 0);
}
sep= above? -fn->yx: fn->sep;
}
if (above && unicode) {
SI min_d= fn->yx / 8;
SI max_d= fn->yx / 3;
if (wideb->y1 + sep < min_d) sep= min_d - wideb->y1;
if (wideb->y1 + sep >= max_d) sep= max_d - wideb->y1;
}
if (!unicode && !wide && !above)
wideb= vresize_box (wideb->ip, wideb, wideb->y1 + fn->yx, wideb->y2);
else if (unicode && s == "<vect>") {
if (wide);
else if (above) sep -= fn->yx + (fn->sep >> 1);
else wideb= vresize_box (wideb->ip, wideb, wideb->y1 + fn->yx, wideb->y2);
}
else if (stix || tex_gyre) sep += fn->sep >> 1;
return wide;
}
To complete the description we discuss wide_box and wide_stix_box which are variants of the same logic:
box
wide_box (path ip, string s, font fn, pencil pen, SI width) {
string r= get_wide (s, fn, width);
metric ex;
fn->get_extents (r, ex);
box b= text_box (ip, 0, r, fn, pen);
return macro_box (ip, b, fn);
}
box
wide_stix_box (path ip, string s, font fn, pencil pen, SI width) {
string r= get_wide_stix (s, fn, width);
metric ex;
fn->get_extents (r, ex);
box b= text_box (ip, 0, r, fn, pen);
return macro_box (ip, b, fn);
}
the concrete selection of the appropriate glyph which fits the
horizontal size of wide construction is performed by get_wide
(or get_stix_wide):
static string
get_wide (string s, font fn, SI width) {
ASSERT (N(s) >= 2 && s[0] == '<' && s[N(s)-1] == '>',
"invalid rubber character");
string radical= s (0, N(s)-1) * "-";
string first = radical * "0>";
metric ex;
fn->get_extents (first, ex);
if ((ex->x2- ex->x1) >= width) return first;
string second = radical * "1>";
metric ey;
fn->get_extents (second, ey);
SI w1= ex->x2- ex->x1;
SI w2= ey->x2- ey->x1;
if ((w2 <= w1) || (w2 > width)) return first;
SI d= w2- w1;
int n= (width-w1) / (d+1);
int credit= 20;
while (true) {
string test= radical * as_string (n+1) * ">";
fn->get_extents (test, ey);
if (ey->x2- ey->x1 > width || credit <= 0)
return radical * as_string (n) * ">";
n++;
credit--;
}
}
static string
get_wide_stix (string s, font fn, SI width) {
ASSERT (N(s) >= 2 && s[0] == '<' && s[N(s)-1] == '>',
"invalid rubber character");
string radical= s (0, N(s)-1) * "-";
metric ex;
int n= 0;
while (true) {
string test= radical * as_string (n) * ">";
fn->get_extents (test, ex);
if (ex->x2- ex->x1 > width || n >= 6)
return radical * as_string (n) * ">";
n++;
}
}
4.6.Subscripts and superscripts
The positioning of subscripts and superscripts is a complicated affair,
due to the conflict between locally and globally optimal esthetics
mentioned above. The base line for a subscript is determined as follows:
-
Always pretend that the subscript has height at least y2-yshift
in the script font (actually we should use the height of an 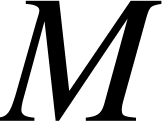 instead).
instead).
-
Try to position the script at the base line given by the main
argument.
-
If the top limit (given by the main argument) is physically exceeded
by the subscript, then the base line is moved further down
accordingly.
The base line for a superscript is determined as follows:
-
Try to physically position the superscript beneath the suggested top
line. Usually, this will place the superscript to far down.
-
Move the superscript up to the logical base line if necessary. This
will usually occur: most of the time, the logical base line is the
just the height of an  -script
below the suggested top line.
-script
below the suggested top line.
-
If the superscript physically descends below the physical under
limit given by the main box, then we move the superscript further
upwards.
If both a subscript and a superscript were present, then we still have
to adjust the base lines: if the top of the subscript and the bottom of
the superscript are not physically separated by sep,
then we both move the subscript and the superscript by the same amount
away from each other. Because of step 1 in the positioning of the
subscript, the base lines of double scripts will usually be the same in
formulas with several of them.
The right slope and italic correction of a script box may be non
trivial. In order to compute them, we first determine the script (or
main argument), whose right limit (taking into account its italic
correction) is furthest to the right (this may be the main box, in the
case of a big integral with a tiny subscript). Then the right slope of
the main box is inherited by the right slope of this script (or main
argument). As to the italic correction, it is precisely the difference
between the right offset of the script plus its italic correction minus
the logical right coordinate of the entire box. The italic correction
should be at least zero though. The left slope and italic correction are
computed in a similar way.
[Explain the code below]
void
concater_rep::typeset_script (tree t, path ip, bool right) {
if (N(t) != 1) { typeset_error (t, ip); return; }
int type= RSUP_ITEM;
box b1, b2;
tree old_ds= env->local_begin (MATH_DISPLAY, "false");
tree old_mc= env->local_begin (MATH_CONDENSED, "true");
tree old_il= env->local_begin_script ();
if (is_func (t, SUB (right))) {
tree old_vp= env->local_begin (MATH_VPOS, "-1");
b1= typeset_as_concat (env, t[0], descend (ip, 0));
type= right? RSUB_ITEM: LSUB_ITEM;
env->local_end (MATH_VPOS, old_vp);
}
if (is_func (t, SUP (right))) {
tree old_vp= env->local_begin (MATH_VPOS, "1");
b2= typeset_as_concat (env, t[0], descend (ip, 0));
type= right? RSUP_ITEM: LSUP_ITEM;
env->local_end (MATH_VPOS, old_vp);
}
env->local_end_script (old_il);
env->local_end (MATH_CONDENSED, old_mc);
env->local_end (MATH_DISPLAY, old_ds);
if (right) penalty_max (HYPH_INVALID);
a << line_item (type, OP_SKIP,
script_box (ip, b1, b2, env->fn), HYPH_INVALID);
// do not use print, because of italic space
if (!right) penalty_max (HYPH_INVALID);
}
dummy_script_box_rep::dummy_script_box_rep (path ip, box b1, box b2, font fn2):
composite_box_rep (ip), fn (fn2)
{
SI sep = fn->sep;
SI lo_y = fn->ysub_lo_base;
SI hi_y = fn->ysup_lo_base;
SI miny2= (fn->y2 - fn->yshift) * script (fn->size, 1) / fn->size;
type= 0;
if (!is_nil (b1)) type += 1;
if (!is_nil (b2)) type += 2;
if ((!is_nil (b1)) && (!is_nil (b2))) {
SI y= max (b1->y2, miny2);
SI d= lo_y + y + sep - hi_y - b2->y1;
if (d > 0) {
lo_y -= (d>>1);
hi_y += (d>>1);
}
}
if (!is_nil (b1)) {
insert (b1, 0, lo_y);
italic_correct (b1);
}
if (!is_nil (b2)) {
insert (b2, 0, hi_y);
italic_correct (b2);
}
position ();
if (!is_nil (b1)) italic_restore (b1);
if (!is_nil (b2)) italic_restore (b2);
left_justify ();
y1= min (y1, fn->ysub_lo_base);
y2= max (y2, fn->ysup_lo_base + fn->yx);
finalize ();
}
4.7.Big operators
Big operators, like the big sum, products or integrals
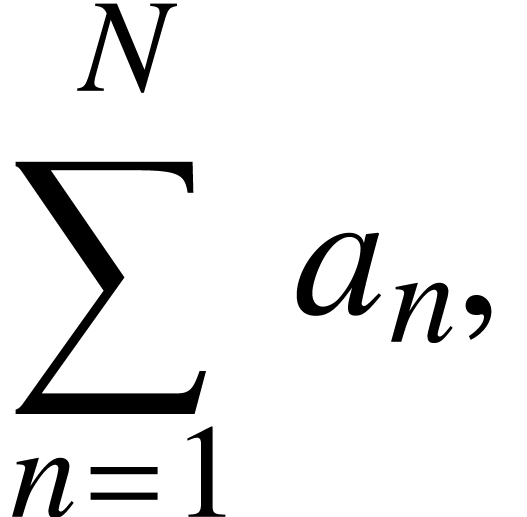
|
<big|sum><rsub|n=1><rsup|N>a<rsub|n>
|
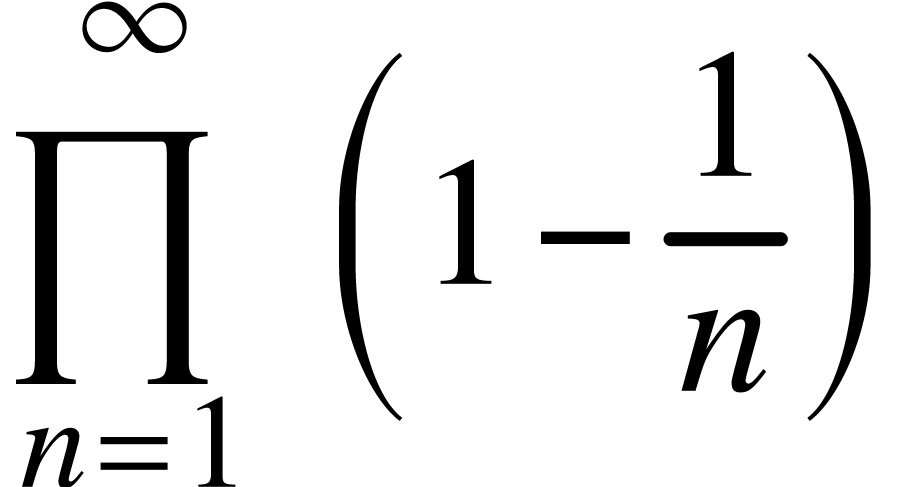
|
<big|prod><rsub|n=1><rsup|\<infty\>>
<around*|(|1-<frac|1|n>|)>
|
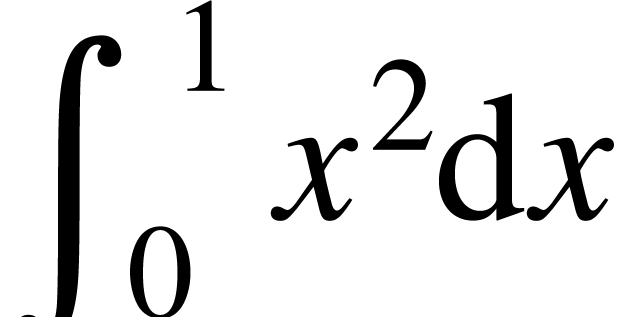
|
<big|int>x<rsup|2>\<mathd\>x
|
It has two basic shapes, either in display style as above or inline as
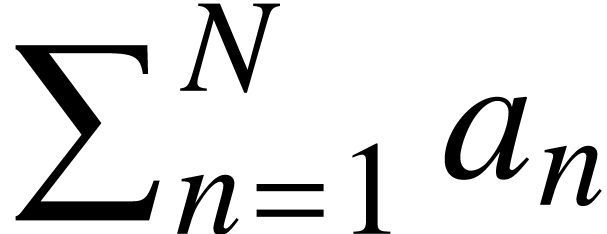 ,
, 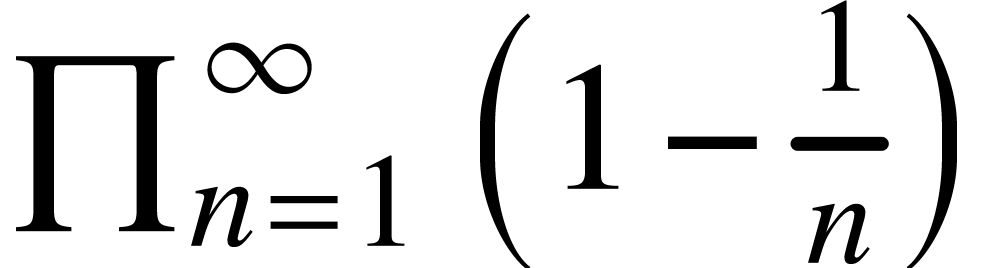 ,
, 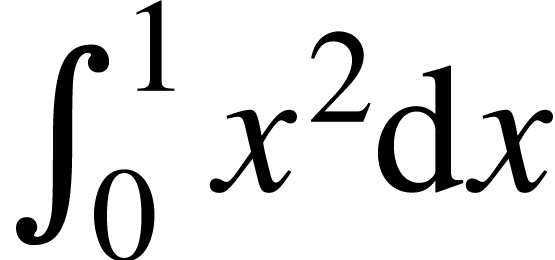 .
.
They are typeset by:
void
concater_rep::typeset_bigop (tree t, path ip) {
if ((N(t) == 1) && is_atomic (t[0])) {
space spc= env->fn->spc;
string l= t[0]->label;
string s= "<big-" * l * ">";
bool flag= (!env->math_condensed) && (l != ".");
box b;
if (env->fn->type == FONT_TYPE_UNICODE) {
font mfn= rubber_font (env->fn);
b= big_operator_box (ip, s, mfn, env->pen,
env->display_style? 2: 1);
}
else b= big_operator_box (ip, s, env->fn, env->pen,
env->display_style? 2: 1);
print (STD_ITEM, OP_BIG, b);
penalty_min (HYPH_PANIC);
bool int_flag= false, it_flag= false, lim_flag= true;
get_big_flags (l, int_flag, it_flag, lim_flag);
if (lim_flag) with_limits (LIMITS_DISPLAY);
if (flag) {
if (int_flag) {
if (env->fn->math_type == MATH_TYPE_STIX)
print (env->display_style? (spc / 2): (spc / 4));
else if (env->fn->math_type == MATH_TYPE_TEX_GYRE)
print (env->display_style? (spc / 2): (spc / 4));
else if (it_flag)
print (env->display_style? 0: (spc / 4));
else print (spc / 4);
}
else print (env->display_style? spc: (spc / 2));
}
// FIXME: we should use parameters from operator-big class in std-math.syx
// FIXME: in concat_post, we add some more space behind big operators
// with scripts; this should be understood better and formalized
}
else typeset_error (t, ip);
}
where we note the handling of limits and of the correct spacing after
the symbol. The relevant glyph for <big|sum> is
<big-sum-N> where N=1,2 according
to the appropriate size. Note that for Unicode fonts (type ==
FONT_TYPE_UNICODE) we dispatch the selection of the glyph to a
rubber obtained via rubber_font.
The function big_operator_box takes care of the proper
vertical placement of the glyph:
box
big_operator_box (path ip, string s, font fn, pencil pen, int n) {
ASSERT (N(s) >= 2 && s[0] == '<' && s[N(s)-1] == '>',
"invalid rubber character");
string r= s (0, N(s)-1) * "-" * as_string (n) * ">";
metric ex;
fn->get_extents (r, ex);
SI y= fn->yfrac - ((ex->y1 + ex->y2) >> 1);
box mvb= move_box (ip, text_box (ip, 0, r, fn, pen), 0, y, false, true);
return macro_box (ip, mvb, fn, BIG_OP_BOX);
}
4.8.Big delimiters
The automatic positioning and computation of sizes of big delimiters is
again complicated because of potential conflicts between locally and
globally optimal esthetics.
First of all, TeX fonts come only with a discrete set of possible sizes
for large delimiters. This is an advantage from the point of view that
it favorites delimiters around slightly different expressions to have
the same baselines. However, it has the disadvantage that delimiters are
easily made “one size to large”. For this reason, we
actually diminish the height and the depth of the delimited expression
by the small amount sep, before computing the sizes of
the delimiters.
Secondly, it is best when the vertical middles of big delimiters occur
at the height of fraction bars. However, in a formula like
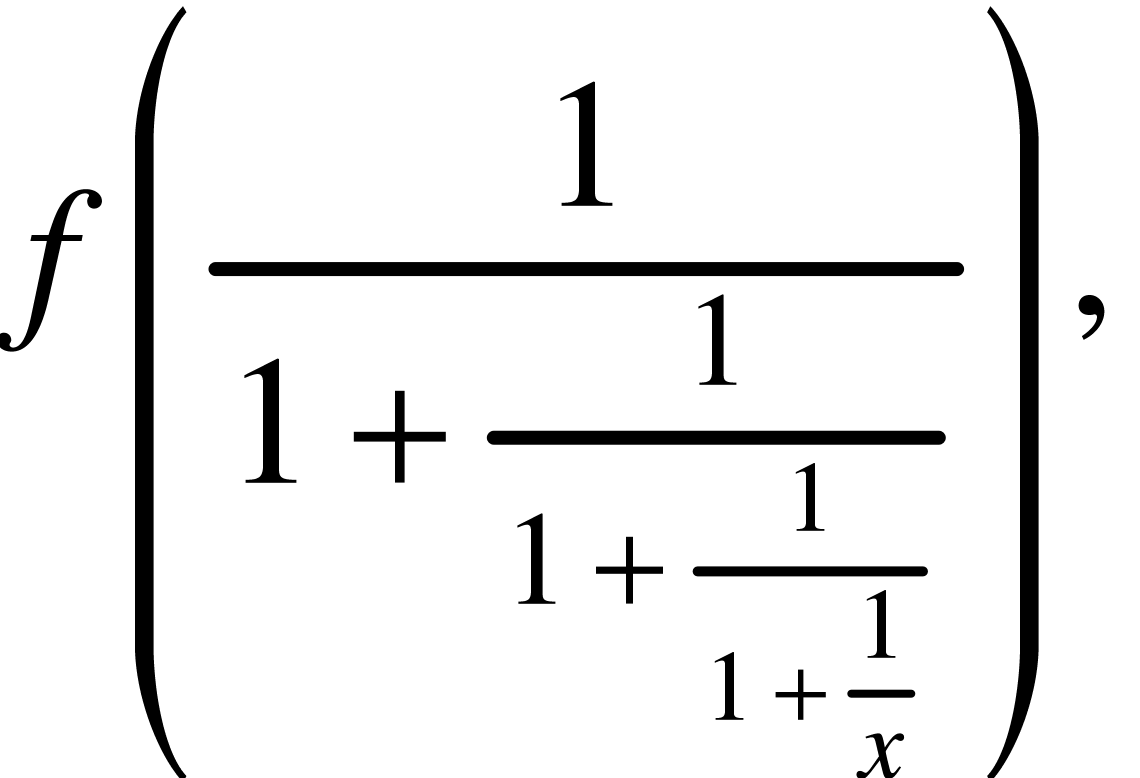
it may be worth it to descend the delimiters a bit. On the other hand,
slight vertical shifts in the middles of the delimiters potentially have
a bad effect on base lines, like in
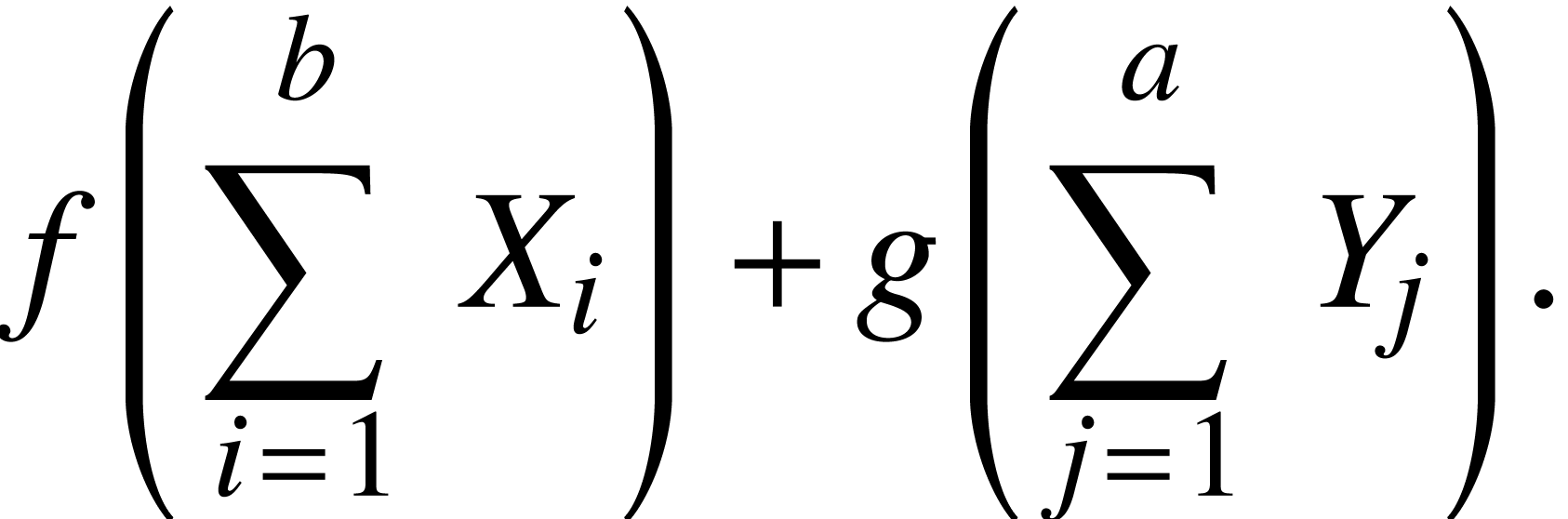
In TeXmacs, we use the following compromise: we start with the middle of
the delimited expression as a first approximation to the middle of the
delimiters. The real middle is obtained by shifting this middle towards
the height of fraction bars by an amount which cannot exceed sep.
From a horizontal point of view, we finally have to notice that we
adapted the metrics of the big delimiters in a way that potential
scripts are positioned in a better way. For instance, according to the
TeX tfm file, in a formula like
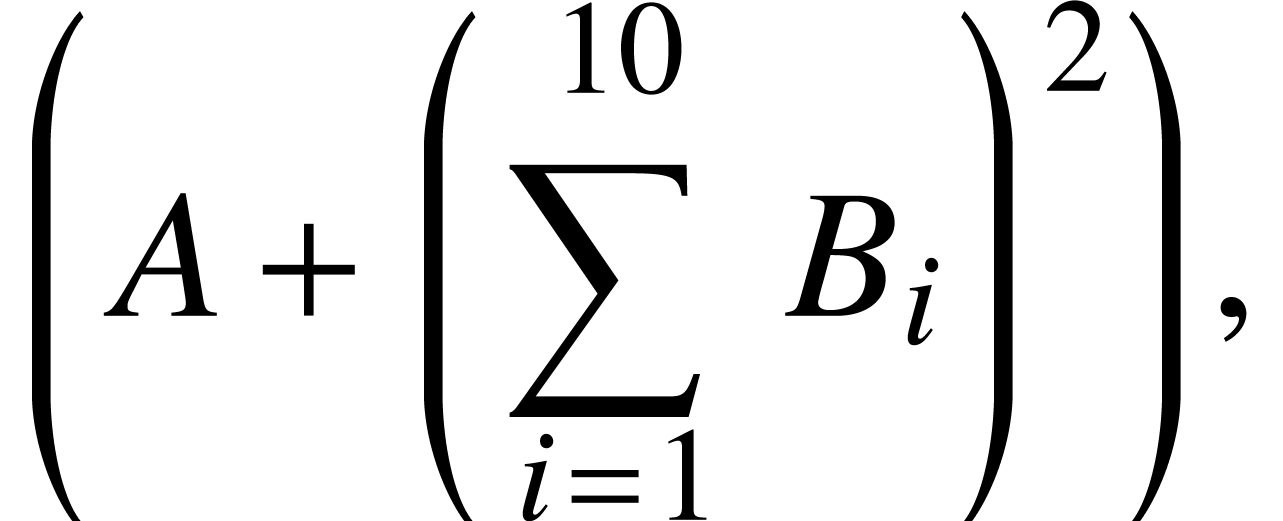
the square rather seems to be a left superscript of the second closing
bracket than a right superscript of the first one. This is particularly
annoying in the case of automatically generated formulas, where this
situation occurs quite often.
Markup looks like
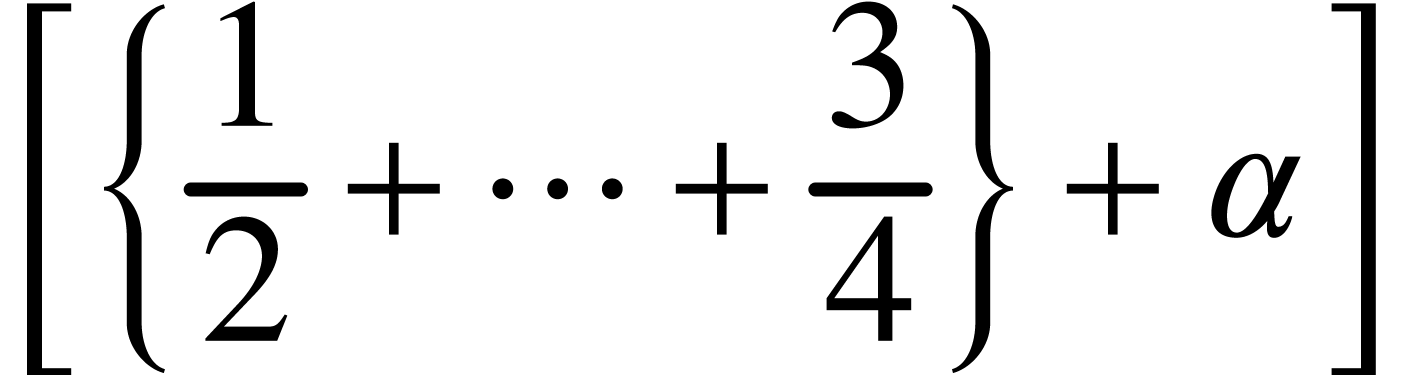
|
<around*|[|
<around*|{|
<frac|1|2>+\<cdots\>+<frac|3|4>
|}>+\<alpha\>
|]>
|
for automatic sizing of the brackets and like
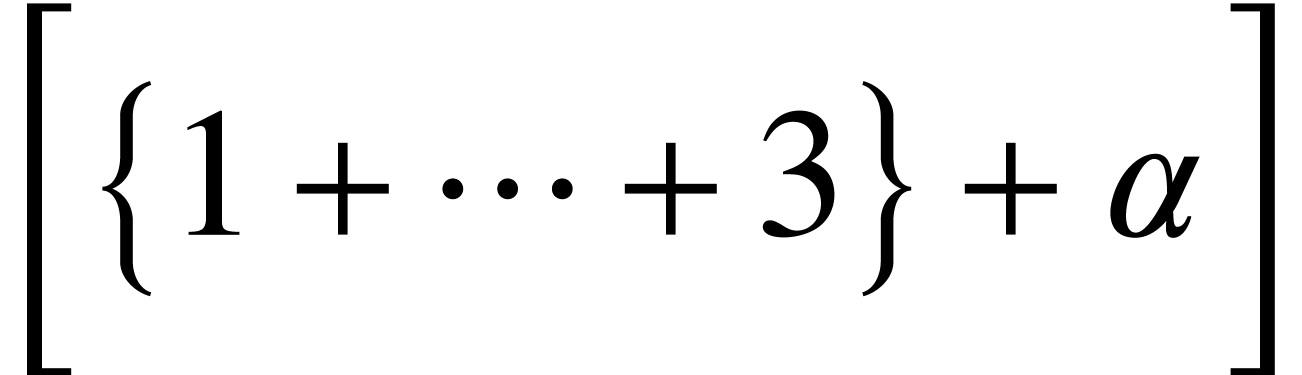
|
<around*|<left|[|5>|
<around*|<left|{|2>|
1+\<cdots\>+3
|<right|}|2>>+\<alpha\>
|<right|]|5>>
|
for manual sizing. The typesetting of big delimiters proceeds in various
phases. A first phase fixes the basic structure and horizontal
positioning of the three arguments of the around tag. If
requested via an appropriate environment variable, we use different
colors to emphasize the matching brackets.
void
concater_rep::typeset_around (tree t, path ip, bool colored) {
tree old_nl=
env->local_begin (MATH_NESTING_LEVEL, as_string (env->nesting_level + 1));
if (colored) {
tree old_col= env->local_begin (COLOR, bracket_color (env->nesting_level));
typeset_around (t, ip, false);
env->local_end (COLOR, old_col);
}
else {
marker (descend (ip, 0));
switch (L(t)) {
case AROUND:
if (N(t) == 3) {
box br1= typeset_as_concat (env, t[0], descend (ip, 0));
print (STD_ITEM, OP_OPENING_BRACKET, br1);
typeset (t[1], descend (ip, 1));
box br2= typeset_as_concat (env, t[2], descend (ip, 2));
print (STD_ITEM, OP_CLOSING_BRACKET, br2);
}
else typeset_error (t, ip);
break;
case VAR_AROUND:
if (N(t) == 3) {
font old_fn= env->fn;
font new_fn= env->fn;
if (starts (new_fn->res_name, "stix-"))
//if (new_fn->type == FONT_TYPE_UNICODE)
new_fn= rubber_font (new_fn);
env->fn= new_fn;
typeset (make_large (LEFT, t[0]),
decorate_middle (descend (ip, 0)));
env->fn= old_fn;
typeset (t[1], descend (ip, 1));
env->fn= new_fn;
typeset (make_large (RIGHT, t[2]),
decorate_middle (descend (ip, 2)));
env->fn= old_fn;
}
else typeset_error (t, ip);
break;
case BIG_AROUND:
if (N(t) == 2) {
typeset (make_large (BIG, t[0]),
decorate_middle (descend (ip, 0)));
typeset (t[1], descend (ip, 1));
}
else typeset_error (t, ip);
break;
default:
break;
}
marker (descend (ip, 1));
}
env->local_end (MATH_NESTING_LEVEL, old_nl);
}
The expression make_large (LEFT, t[0]) ensures that the
first and third subtrees have a specific structure, of the form <left|[|5> for a fixed size or <left|[>
if there is automatic sizing.
static tree
make_large (tree_label l, tree t) {
if (!is_atomic (t)) {
if (is_func (t, l)) {
if (N(t) == 2 && is_atomic (t[0]) && is_int (t[1])) {
string s= t[0]->label;
if (N(s) >= 3 && s[0] == '<' && s[N(s)-1] == '>') s= s (1, N(s)-1);
return tree (l, s * "-" * t[1]->label);
}
else return t;
}
else return tree (l, ".");
}
string s= t->label;
if (N(s) <= 1) return tree (l, s);
if (s[0] != '<' || s[N(s)-1] != '>' || s == "<nobracket>")
return tree (l, ".");
return tree (l, s (1, N(s)-1));
}
The typesetting of LEFT, RIGHT and MID markup is dispatched as follows in concater_rep::typeset:
case LEFT:
typeset_large (t, ip, LEFT_BRACKET_ITEM, OP_OPENING_BRACKET, "<left-");
break;
case MID:
typeset_wide_middle (t, ip);
break;
case RIGHT:
typeset_large (t, ip, RIGHT_BRACKET_ITEM, OP_CLOSING_BRACKET, "<right-");
break;
and realised as follows:
void
concater_rep::typeset_large (tree t, path ip, int tp, int otp, string prefix) {
font old_fn= env->fn;
if (starts (old_fn->res_name, "stix-"))
//if (old_fn->type == FONT_TYPE_UNICODE)
env->fn= rubber_font (old_fn);
if (N(t) < 1 || !is_atomic (t[0]))
typeset_error (t, ip);
else {
string br= t[0]->label;
if (N(br) > 2 && br[0] == '<' && br[N(br)-1] == '>')
br= br (1, N(br) - 1);
if (N(t) == 1) {
string s= prefix * br * ">";
box b= text_box (ip, 0, s, env->fn, env->pen);
print (tp, otp, b);
// temporarary: use parameters from group-open class in std-math.syx
// bug: allow hyphenation after ) and before *
}
else if (N(t) == 2 && is_int (t[1])) {
int nr= max (as_int (t[1]->label), 0);
string s= prefix * br * "-" * as_string (nr) * ">";
box b= text_box (ip, 0, s, env->fn, env->pen);
SI dy= env->fn->yfrac - ((b->y1 + b->y2) >> 1);
box mvb= move_box (ip, b, 0, dy, false, true);
print (STD_ITEM, otp, macro_box (ip, mvb, env->fn));
}
else {
SI y1, y2;
if (N(t) == 2) {
SI l= env->as_length (t[1]) >> 1;
y1= env->fn->yfrac - l;
y2= env->fn->yfrac + l;
}
else {
y1= env->as_length (t[1]);
y2= env->as_length (t[2]);
}
string s= prefix * br * ">";
box b= delimiter_box (ip, s, env->fn, env->pen, y1, y2);
print (STD_ITEM, otp, b);
}
}
env->fn= old_fn;
}
Note that the main branch for markup like <left|[>
produces only a text box with an appropriate glyph. The vertical size of
the glyph is still not correct at this point. Since it depends on the
globality of the current expression and not known when typesetting the
left bracket. It will be determined later on. See Section 4.11.
4.9.Long arrows
Long arrows refers to the following markup:
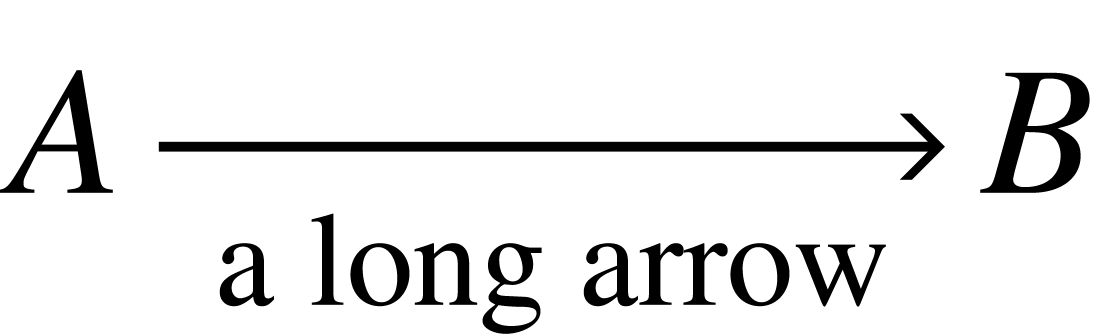
|
A<long-arrow|<rubber-rightarrow>||<text|a long arrow>>B
|
allowing for material above and below. The typesetting of long arrows do
not require further mechanisms to those already put in place for wide
boxes:
void
concater_rep::typeset_long_arrow (tree t, path ip) {
if (N(t) != 2 && N(t) != 3) { typeset_error (t, ip); return; }
tree old_ds= env->local_begin (MATH_DISPLAY, "false");
tree old_mc= env->local_begin (MATH_CONDENSED, "true");
tree old_il= env->local_begin_script ();
box sup_b, sub_b;
if (N(t) >= 2) {
tree old_vp= env->local_begin (MATH_VPOS, "-1");
sup_b= typeset_as_concat (env, t[1], descend (ip, 1));
env->local_end (MATH_VPOS, old_vp);
}
if (N(t) >= 3) {
tree old_vp= env->local_begin (MATH_VPOS, "1");
sub_b= typeset_as_concat (env, t[2], descend (ip, 2));
env->local_end (MATH_VPOS, old_vp);
}
env->local_end_script (old_il);
env->local_end (MATH_CONDENSED, old_mc);
env->local_end (MATH_DISPLAY, old_ds);
string s= env->exec_string (t[0]);
SI w= sup_b->w();
if (N(t) == 3) w= max (w, sub_b->w());
w += env->fn->wquad;
box arrow= wide_box (decorate (descend (ip, 0)), s, env->fn, env->pen, w);
space spc= env->fn->spc;
if (env->math_condensed) spc= space (spc->min>>3, spc->def>>3, spc->max>>2);
else spc= space (spc->min>>1, spc->def>>1, spc->max);
print (spc);
print (limit_box (ip, arrow, sub_b, sup_b, env->fn, false));
print (spc);
}
It introduces lim_box_rep which takes care of the
relative positioning of the various subboxes (limit_box
returns a lim_box_rep):
lim_box_rep::lim_box_rep (path ip, box r2, box lo, box hi, font fn2, bool gl):
composite_box_rep (ip), ref (r2), fn (fn2), glued (gl)
{
SI sep_lo= fn->sep + fn->yshift;
SI sep_hi= fn->sep + (fn->yshift >> 1);
SI X, Y;
insert (ref, 0, 0);
type= 0;
if (!is_nil (lo)) type += 1;
if (!is_nil (hi)) type += 2;
if (!is_nil (lo)) {
SI top= max (lo->y2, fn->y2 * script (fn->size, 1) / fn->size) + sep_lo;
Y= ref->y1;
X= ((SI) (ref->right_slope ()* (Y+top-lo->y1))) + ((ref->x1+ref->x2)>>1);
insert (lo, X- (lo->x2 >> 1), Y-top);
italic_correct (lo);
}
if (!is_nil (hi)) {
SI bot= min (hi->y1, fn->y1 * script (fn->size, 1) / fn->size) - sep_hi;
Y= ref->y2;
X= ((SI) (ref->right_slope ()*(Y+hi->y2-bot))) + ((ref->x1+ref->x2)>>1);
insert (hi, X- (hi->x2 >> 1), Y-bot);
italic_correct (hi);
}
italic_correct (ref);
position ();
italic_restore (ref);
if (!is_nil (lo)) italic_restore (lo);
if (!is_nil (hi)) italic_restore (hi);
left_justify ();
finalize ();
}
4.10.Above and below boxes
The below and above tags are
used to explicitly attach a script below or
above a given content. Both can be mixed in
order to produce content with both a script below and above:

|
<math| <above|<below|xor|i=1>|∞>
x<rsub|i>>
|
Like long arrows, above and below tags also rely on lim_box_rep
for their graphical rendering:
void
concater_rep::typeset_below (tree t, path ip) {
if (N(t) != 2) { typeset_error (t, ip); return; }
box b1= typeset_as_concat (env, t[0], descend (ip, 0));
tree old_ds= env->local_begin (MATH_DISPLAY, "false");
tree old_mc= env->local_begin (MATH_CONDENSED, "true");
tree old_il= env->local_begin_script ();
box b2= typeset_as_concat (env, t[1], descend (ip, 1));
env->local_end_script (old_il);
env->local_end (MATH_CONDENSED, old_mc);
env->local_end (MATH_DISPLAY, old_ds);
print (limit_box (ip, b1, b2, box (), env->fn, false));
}
void
concater_rep::typeset_above (tree t, path ip) {
if (N(t) != 2) { typeset_error (t, ip); return; }
box b1= typeset_as_concat (env, t[0], descend (ip, 0));
tree old_ds= env->local_begin (MATH_DISPLAY, "false");
tree old_mc= env->local_begin (MATH_CONDENSED, "true");
tree old_il= env->local_begin_script ();
box b2= typeset_as_concat (env, t[1], descend (ip, 1));
env->local_end_script (old_il);
env->local_end (MATH_CONDENSED, old_mc);
env->local_end (MATH_DISPLAY, old_ds);
// NOTE: start dirty hack to get scripts above … right
if ((t[0] == "<ldots>" && env->read ("low-dots") != UNINIT) ||
(t[0] == "<cdots>" && env->read ("center-dots") != UNINIT)) {
string s= (t[0] == "<ldots>"? ",": "<cdot>");
box tb= typeset_as_concat (env, s, decorate_middle (descend (ip, 0)));
b1= resize_box (descend (ip, 0), b1, b1->x1, b1->y1, b1->x2, tb->y2);
}
// NOTE: end dirty hack to get scripts above … right
print (limit_box (ip, b1, box (), b2, env->fn, false));
}
4.11.Finalization
The computation of the correct size of extensible brackets and the
proper placement of super/sub-scripts require a second pass through the
line_item array that concater is
currently typesetting. This triggered by concater_rep::finish
():
void
concater_rep::finish () {
kill_spaces ();
pre_glue ();
handle_brackets ();
clean_and_correct ();
}
kill_spaces and pre_glue simplify the
line_items array:
/******************************************************************************
* Kill invalid spaces
******************************************************************************/
void
concater_rep::kill_spaces () {
int i;
for (i=N(a)-1; (i>0) && (a[i]->type == CONTROL_ITEM); i--)
a[i-1]->spc= space (0);
for (i=0; (i<N(a)) && (a[i]->type == CONTROL_ITEM); i++)
a[i]->spc= space (0);
for (i=0; i<N(a); i++)
if (a[i]->type==CONTROL_ITEM) {
if (is_formatting (a[i]->t)) {
tree_label lab= L(a[i]->t);
if ((lab==NEXT_LINE) || (lab==LINE_BREAK) || (lab==NEW_LINE))
{
if (i>0) a[i-1]->spc= space (0);
a[i]->spc= space (0);
}
}
if (is_tuple (a[i]->t, "env_par") ||
is_tuple (a[i]->t, "env_page"))
a[i]->spc= space (0);
}
}
while pre_glue put together neightbor sub and super
scripts on the same side labelling them with the line items type GLUE_LSUBS_ITEM or GLUE_RSUBS_ITEM:
void
concater_rep::pre_glue () {
int i=0;
while (true) {
int j= succ(i);
if (j >= N(a)) break;
line_item item1= a[i];
line_item item2= a[j];
int t1= item1->type;
int t2= item2->type;
if (((t1 == RSUB_ITEM) && (t2 == RSUP_ITEM)) ||
((t1 == RSUP_ITEM) && (t2 == RSUB_ITEM)) ||
((t1 == LSUB_ITEM) && (t2 == LSUP_ITEM)) ||
((t1 == LSUP_ITEM) && (t2 == LSUB_ITEM)))
{
bool flag1 = (t1 == LSUB_ITEM) || (t1 == RSUB_ITEM);
bool flag2 = (t1 == LSUB_ITEM) || (t1 == LSUP_ITEM);
int type = flag2? GLUE_LSUBS_ITEM: GLUE_RSUBS_ITEM;
box b1 = flag1? item1->b[0]: item2->b[0];
box b2 = flag1? item2->b[0]: item1->b[0];
box b = script_box (b1->ip, b1, b2, env->fn);
int pen = item2->penalty;
space spc = max (item1->spc, item2->spc);
a[i]= line_item (type, OP_SKIP, b, pen);
a[i]->spc = spc;
for (int k=i+1; k<j; k++)
if (a[k]->type == MARKER_ITEM)
a[k]= line_item (OBSOLETE_ITEM, OP_SKIP, a[k]->b, a[k]->penalty);
a[j]= line_item (OBSOLETE_ITEM, OP_SKIP, item2->b, pen);
}
i++;
}
}
The function handle_brackets fixes the size of the
extensible brackets and middle marks and also the global placement of
scripts :
void
concater_rep::handle_brackets () {
int first=-1, start=0, i=0;
while (i<N(a)) {
if (a[i]->type==LEFT_BRACKET_ITEM) {
if (first==-1) first= i;
start= i;
}
if (a[i]->type==RIGHT_BRACKET_ITEM) {
handle_scripts (succ (start), prec (i));
handle_matching (start, i);
if (first!=-1) i=first-1;
start= 0;
first= -1;
}
i++;
}
if (N(a)>0) {
handle_scripts (0, N(a)-1);
handle_matching (0, N(a)-1);
}
}
The placement of scripts is the job of handle_scripts:
void
concater_rep::handle_scripts (int start, int end) {
int i;
for (i=start; i<=end; ) {
if ((a[i]->type == OBSOLETE_ITEM) ||
(a[i]->type == LSUB_ITEM) ||
(a[i]->type == LSUP_ITEM) ||
(a[i]->type == GLUE_LSUBS_ITEM) ||
(a[i]->type == RSUB_ITEM) ||
(a[i]->type == RSUP_ITEM) ||
(a[i]->type == GLUE_RSUBS_ITEM) ||
(a[i]->type == CONTROL_ITEM && L(a[i]->t) == DATOMS)) {
i++; continue; }
path sip;
int l= prec (i);
box lb1, lb2;
if (l < start) l= -1;
else switch (a[l]->type) {
case LSUB_ITEM:
lb1= a[l]->b[0]; sip= lb1->ip;
break;
case LSUP_ITEM:
lb2= a[l]->b[0]; sip= lb2->ip;
break;
case GLUE_LSUBS_ITEM:
lb1= a[l]->b[0]; lb2= a[l]->b[1];
sip= lb2->ip;
break;
default:
l = -1;
}
int r= succ (i);
box rb1, rb2;
if (r > end) r= N(a);
else switch (a[r]->type) {
case RSUB_ITEM:
rb1= a[r]->b[0]; sip= rb1->ip;
break;
case RSUP_ITEM:
rb2= a[r]->b[0]; sip= rb2->ip;
break;
case GLUE_RSUBS_ITEM:
rb1= a[r]->b[0]; rb2= a[r]->b[1];
sip= rb2->ip;
break;
default:
r = N(a);
}
box b;
if (l==-1) {
if (r==N(a)) { i++; continue; }
else {
font ref_fn= get_reference_font (a[i]->b, env->fn);
box mb= glue_right_markers (a[i]->b, i, r, false);
if (a[i]->limits)
b= limit_box (sip, mb, rb1, rb2, ref_fn, true);
else
b= right_script_box (sip, mb, rb1, rb2, ref_fn, env->vert_pos);
glue (b, i, r);
}
}
else {
font ref_fn= get_reference_font (a[i]->b, env->fn);
box mb= glue_left_markers (a[i]->b, i, l);
if (r==N(a)) {
b= left_script_box (sip, mb, lb1, lb2, ref_fn, env->vert_pos);
glue (b, i, l);
}
else {
mb= glue_right_markers (mb, i, r, true);
b = side_box (sip, mb, lb1, lb2, rb1, rb2, ref_fn, env->vert_pos);
glue (b, i, l, r);
}
}
}
}
with the help of the following subsidiary routines: [explain
more]
box
concater_rep::glue_left_markers (box b, int ref, int arg) {
int i= arg+1;
while (i < ref && a[i]->type == OBSOLETE_ITEM) i++;
if (i >= ref) return b;
array<box> bs;
array<SI> spc;
while (i < ref) {
if (a[i]->type == MARKER_ITEM) {
bs << a[i]->b;
spc << 0;
a[i]->type= OBSOLETE_ITEM;
}
i++;
}
bs << b;
spc << 0;
return concat_box (b->ip, bs, spc);
}
box
concater_rep::glue_right_markers (box b, int ref, int arg, bool flag) {
int i= ref+1;
while (i < arg && a[i]->type == OBSOLETE_ITEM) i++;
if (i >= arg) return b;
array<box> bs;
array<SI> spc;
if (flag) {
for (int j=0; j<N(b); j++) {
bs << b[j];
spc << 0;
}
}
else {
bs << b;
spc << 0;
}
while (i < arg) {
if (a[i]->type == MARKER_ITEM) {
bs << a[i]->b;
spc << 0;
a[i]->type= OBSOLETE_ITEM;
}
i++;
}
return concat_box (b->ip, bs, spc);
}
void
concater_rep::glue (box b, int ref, int arg) {
if (a[ref]->op_type == OP_BIG && arg >= ref && !a[ref]->limits) {
font ref_fn= get_reference_font (a[ref]->b, env->fn);
if (ref_fn->math_type != MATH_TYPE_NORMAL)
if (a[ref]->spc->def > 0) {
space spc= ref_fn->spc;
a[ref]->spc += space (spc->min/3, spc->def/3, spc->def/3);
}
}
space spc = max (a[ref]->spc, a[arg]->spc);
a[arg] = line_item (OBSOLETE_ITEM, OP_SKIP, a[arg]->b, a[arg]->penalty);
a[ref] = line_item (arg<ref? GLUE_LEFT_ITEM: GLUE_RIGHT_ITEM,
a[ref]->op_type, b,
min (a[ref]->penalty, a[arg]->penalty));
a[ref]->spc = spc;
}
void
concater_rep::glue (box b, int ref, int arg1, int arg2) {
if (a[ref]->op_type == OP_BIG && !a[ref]->limits) {
font ref_fn= get_reference_font (a[ref]->b, env->fn);
if (ref_fn->math_type != MATH_TYPE_NORMAL)
if (a[ref]->spc->def > 0) {
space spc= ref_fn->spc;
a[ref]->spc += space (spc->min/3, spc->def/3, spc->def/3);
}
}
space spc = max (a[ref]->spc, max (a[arg1]->spc, a[arg2]->spc));
int pen = min (a[ref]->penalty, min (a[arg1]->penalty, a[arg2]->penalty));
space ref_spc= a[ref]->spc;
a[arg1]= line_item (OBSOLETE_ITEM, OP_SKIP, a[arg1]->b, a[arg1]->penalty);
a[arg2]= line_item (OBSOLETE_ITEM, OP_SKIP, a[arg2]->b, a[arg2]->penalty);
a[ref]= line_item (GLUE_BOTH_ITEM, a[ref]->op_type, b, pen);
a[ref]->spc = spc;
}
Finally, the sizing of the brackets is the job of handle_matching:
void
concater_rep::handle_matching (int start, int end) {
//cout << "matching " << start << " -- " << end << "\n";
//cout << a << "\n\n";
int i;
SI y1= MAX_SI;
SI y2= -MAX_SI;
bool uninit= true;
a[start]->penalty++;
a[end]->penalty++;
for (i=start+1; i<end; i++) {
if (a[i]->type == OBSOLETE_ITEM) continue;
// cout << " " << a[i] << ": " << (a[i]->b->y2- a[i]->b->y1) << "\n";
// y1= min (y1, a[i]->b->sub_base());
// y2= max (y2, a[i]->b->sup_base());
SI lo, hi;
a[i]->b->get_bracket_extents (lo, hi);
y1= min (y1, lo);
y2= max (y2, hi);
a[i]->penalty++;
uninit= false;
}
if (uninit) {
y1= min (a[start]->b->y1, a[end]->b->y2);
y2= max (a[start]->b->y1, a[end]->b->y2);
}
for (i=start; i<=end; i++) {
int tp= a[i]->type;
if (tp == LEFT_BRACKET_ITEM ||
tp == MIDDLE_BRACKET_ITEM ||
tp == RIGHT_BRACKET_ITEM)
{
string ls= a[i]->b->get_leaf_string ();
pencil lp= a[i]->b->get_leaf_pencil ();
font fn= a[i]->b->get_leaf_font ();
// find the middle of the bracket, around where to center
SI mid= (a[i]->b->y1 + a[i]->b->y2) >> 1;
bool custom=
N(ls) > 2 && is_digit (ls[N(ls)-2]) && !ends (ls, "-0>");
if (custom) {
int pos= N(ls)-1;
while (pos > 0 && ls[pos] != '-') pos--;
if (pos > 0 && ls[pos-1] == '-') pos--;
string ss= ls (0, pos) * ">";
box auxb= text_box (a[i]->b->ip, 0, ss, fn, lp);
mid= (auxb->y1 + auxb->y2) >> 1;
}
// make symmetric and prevent from too large delimiters if possible
SI Y1 = y1 + (fn->sep >> 1);
SI Y2 = y2 - (fn->sep >> 1);
SI tol = fn->sep << 1;
SI drift= ((Y1 + Y2) >> 1) - mid; // fn->yfrac;
if (drift < 0) Y2 += min (-drift, tol) << 1;
else Y1 -= min (drift, tol) << 1;
// further adjustments when the enclosed expression is not very high
// and for empty brackets
SI h= y2 - y1 - fn->sep;
SI d= 5 * fn->yx - h;
if (d > 0) { Y1 += d/12; Y2 -= d/12; }
if (N(ls) >= 8 && (ls[6] == '.' || ls[7] == '.'))
if (starts (ls, "<left-.") || starts (ls, "<right-.")) {
Y1 += d/6; Y2 -= d/12; }
// replace item by large or small delimiter
if (Y1 < fn->y1 || Y2 > fn->y2 || custom || use_poor_rubber (fn))
a[i]->b= delimiter_box (a[i]->b->ip, ls, fn, lp, Y1, Y2, mid, y1, y2);
else {
string s= "<nobracket>";
int j;
for (j=0; j<N(ls); j++)
if (ls[j] == '-') break;
if (j<N(ls) && ls[N(ls)-1] == '>') s= ls (j+1, N(ls)-1);
if (N(s) > 1 && s[0] != '<') s= "<" * s * ">";
else if (N(s) == 0 || s == ".") s= "<nobracket>";
a[i]->b= text_box (a[i]->b->ip, 0, s, fn, lp);
tp= STD_ITEM;
}
a[i]->type= STD_ITEM;
}
if (tp == LEFT_BRACKET_ITEM)
for (int j= i-1; j>=0; j--) {
if (a[j]->type == MARKER_ITEM) {
SI Y1= a[i]->b->y1;
SI Y2= a[i]->b->y2;
//a[j]->b = marker_box (a[j]->b->find_lip (), 0, Y1, 0, Y2, a[j]->b);
a[j]->b = marker_box (a[j]->b->find_lip (), 0, Y1, 0, Y2, a[i]->b);
a[j]->type= STD_ITEM;
}
else if (a[j]->type != CONTROL_ITEM) break;
}
if (tp == RIGHT_BRACKET_ITEM)
for (int j= i+1; j<N(a); j++) {
if (a[j]->type == MARKER_ITEM) {
SI Y1= a[i]->b->y1;
SI Y2= a[i]->b->y2;
//a[j]->b = marker_box (a[j]->b->find_lip (), 0, Y1, 0, Y2, a[j]->b);
a[j]->b = marker_box (a[j]->b->find_lip (), 0, Y1, 0, Y2, a[i]->b);
a[j]->type= STD_ITEM;
}
else if (a[j]->type != CONTROL_ITEM) break;
}
}
}
Again, a key point of this procedure is the call to delimiter_box
(in src/Typeset/Boxes/Basic/text_boxes.cpp) in order to
replace the “temporary” vertical delimiter, with a correctly
sized one (be it a left, right or middle delimiter).
box
delimiter_box (path ip, string s, font fn, pencil pen,
SI bot, SI top, SI mid, SI real_bot, SI real_top)
{
SI h= top - bot;
string r= get_delimiter (s, fn, h);
box b= text_box (ip, 0, r, fn, pen);
SI x= -b->x1;
SI y= (top + bot - b->y1 - b->y2) >> 1;
if (b->y2 - b->y1 < h) {
y= (mid - b->y1 - b->y2) >> 1;
y= min (top - b->y2, y);
y= max (bot - b->y1, y);
}
//cout << s << ", " << bot/PIXEL << " -- " << top/PIXEL
// << " -> " << r << "; " << x/PIXEL << ", " << y/PIXEL << "\n";
//cout << " extents: " << b->x1/PIXEL << ", " << b->y1/PIXEL
// << "; " << b->x2/PIXEL << ", " << b->y2/PIXEL << "\n";
box mvb= move_delimiter_box (ip, b, x, y, real_bot, real_top);
if (ends (r, "-0>")) return mvb;
SI dy= ((mvb->y1 + mvb->y2)>>1) - fn->yfrac;
return macro_delimiter_box (ip, mvb, fn, dy);
}
The function get_delimiter queries the font for a
sequence of glyphs in the form <left-[-N> (for
example) with N=0,1,2,3,4,... until we obtain the required
height.
/******************************************************************************
* Computing right size for rubber characters
******************************************************************************/
static int
get_number (string s, int& pos) {
int n= N(s);
pos= n-1;
while (pos > 0 && s[pos] != '-') pos--;
if (pos > 0 && s[pos-1] == '-') pos--;
return as_int (s (pos+1, n-1));
}
static string
get_delimiter (string s, font fn, SI height) {
int ns= N(s);
ASSERT (ns >= 2 && s[0] == '<' && s[ns-1] == '>',
"invalid rubber character");
if (is_digit (s[ns-2])) {
int pos;
int plus= get_number (s, pos);
if (pos > 0) {
string s2= s (0, pos) * ">";
string r2= get_delimiter (s2, fn, height);
int pos2;
int nr2= get_number (r2, pos2);
if (pos2 > 0) {
int nr= max (nr2 + plus, 0);
return r2 (0, pos2) * "-" * as_string (nr) * ">";
}
}
}
height -= PIXEL;
string radical= s (0, N(s)-1) * "-";
string best= radical * "0>";
SI best_h= 0;
int n= 0;
SI last= 0;
int credit= 20;
while (credit > 0) {
metric ex;
string test= radical * as_string (n) * ">";
fn->get_extents (test, ex);
SI h= ex->y2 - ex->y1;
if (h >= (height - (n==1? PIXEL: 0))) return test;
if (h > best_h) { best_h= h; best= test; }
int d= h - last;
if (last > 0 && d > 0) {
int plus= (height - h - 1) / d;
if (plus <= 1 || n <= 4) { n++; last= h; }
else {
int n2= n + plus;
metric ex2;
string test2= radical * as_string (n2) * ">";
fn->get_extents (test2, ex2);
SI h2= ex2->y2 - ex2->y1;
if (h2 >= height || h2 < h) { n++; last= h; }
else { n= n2; last= 0; }
}
}
else if (last <= 0 || n < 10) { n++; last= h; }
else return best;
credit--;
}
return best;
}
5.Final remarks
A list of possible improvements to the code reviewed in this document:
-
The mechanism to select appropriate glyphs do not depend on specific
details of the typesetting process apart from the required size, so
maybe can be moved into the font (and possibly allow for
simplification in this generic part)
-
Ideally we want to try to remove dependence on specific fonts in
this part of code, all the required measurements should be available
in a generic way from the current font without further tweaking (or
less of it).
-
Allow for OpenType MATH table information (if
available) to be used, e.g. in the placement of various math
constructions.
 , the bottoms of the
, the bottoms of the  and
and  should be at the same height as the
bottom of the
should be at the same height as the
bottom of the  -part in
the
-part in
the 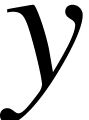 . This should again
be the case in
. This should again
be the case in 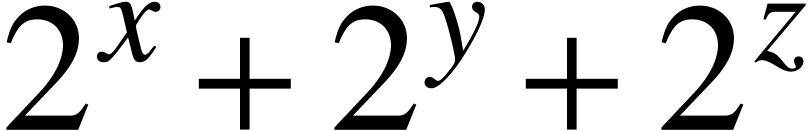 .
.
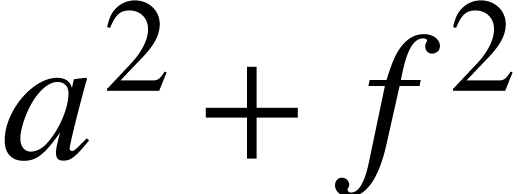 , the typesetter should
notice the hangover of the
, the typesetter should
notice the hangover of the 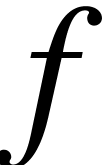 .
This should again be the case in
.
This should again be the case in 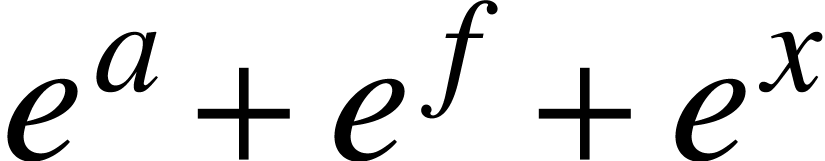 .
Similarly, the distance between the baselines of the
.
Similarly, the distance between the baselines of the  and the
and the  in
in 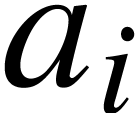 should not be disproportionally large with respect to the height
of an
should not be disproportionally large with respect to the height
of an  .
.
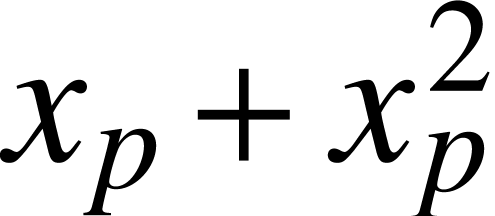 . On the one hand, the baselines of the scripts
should be the same, but the other hand, the first subscript should not
be “disproportionally low” with respect to the
. On the one hand, the baselines of the scripts
should be the same, but the other hand, the first subscript should not
be “disproportionally low” with respect to the  . Unfortunately, this dilemma can not been
solved in a completely satisfactory way without the help of a human for
the simple reason that the computer has no way to know whether the
. Unfortunately, this dilemma can not been
solved in a completely satisfactory way without the help of a human for
the simple reason that the computer has no way to know whether the 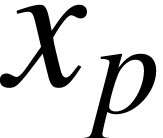 and
and 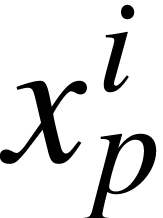 are
“related”. Indeed, if the
are
“related”. Indeed, if the 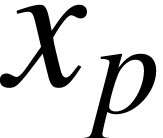 and
and 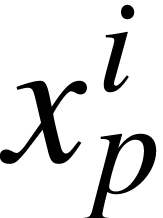 are close (like in
are close (like in 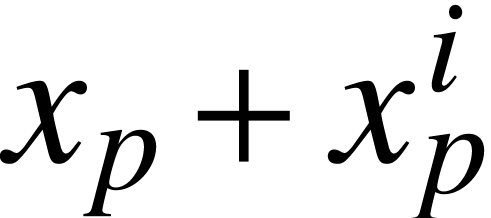 ),
then it is natural to opt for a common base line. However, if they are
further away from each other (like in
),
then it is natural to opt for a common base line. However, if they are
further away from each other (like in  ),
then we might want to opt for different base lines and locally optimize
the rendering of the first
),
then we might want to opt for different base lines and locally optimize
the rendering of the first 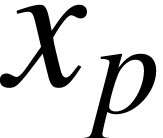 .
.
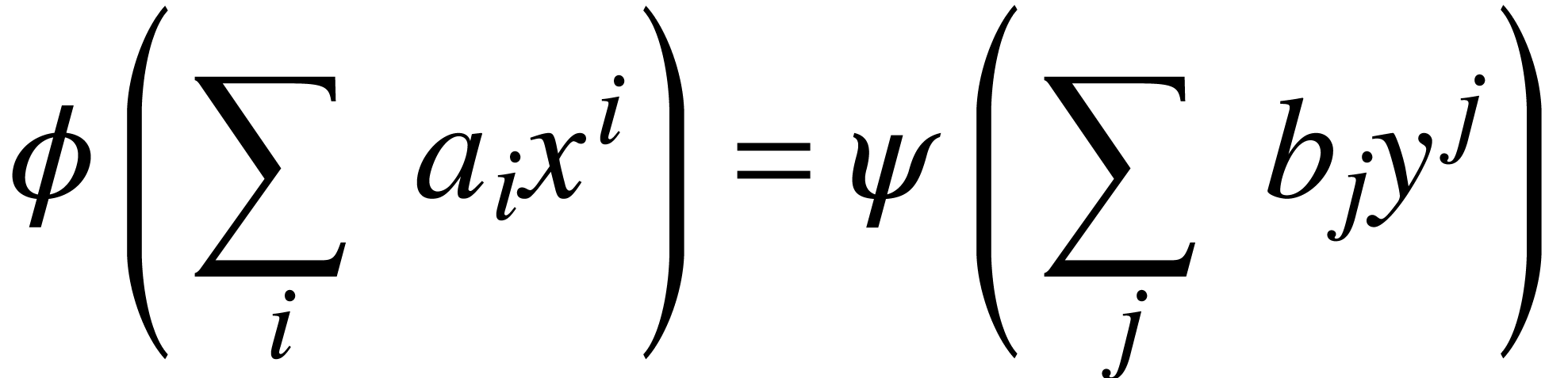
 of the second sum to 0fn.
Alternatively, one may resize the bottoms of both the
of the second sum to 0fn.
Alternatively, one may resize the bottoms of both the  and
and  subscripts to (say) -0.3fn.
For easier adjustments you may use →→ and →→
to automatically adjust the size of the contents to the height of the
character “x” and the largest one in the font respectively.
subscripts to (say) -0.3fn.
For easier adjustments you may use →→ and →→
to automatically adjust the size of the contents to the height of the
character “x” and the largest one in the font respectively.
 subscript of the sum.
However, this would alter the meaning of the formula (whence make it non
suitable as input to a computer algebra system) In the future, we plan
to provide additional constructs in order to facilitate structural
adjusting. For instance, in the case of a formula like
subscript of the sum.
However, this would alter the meaning of the formula (whence make it non
suitable as input to a computer algebra system) In the future, we plan
to provide additional constructs in order to facilitate structural
adjusting. For instance, in the case of a formula like
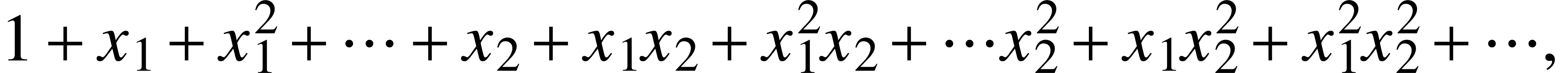
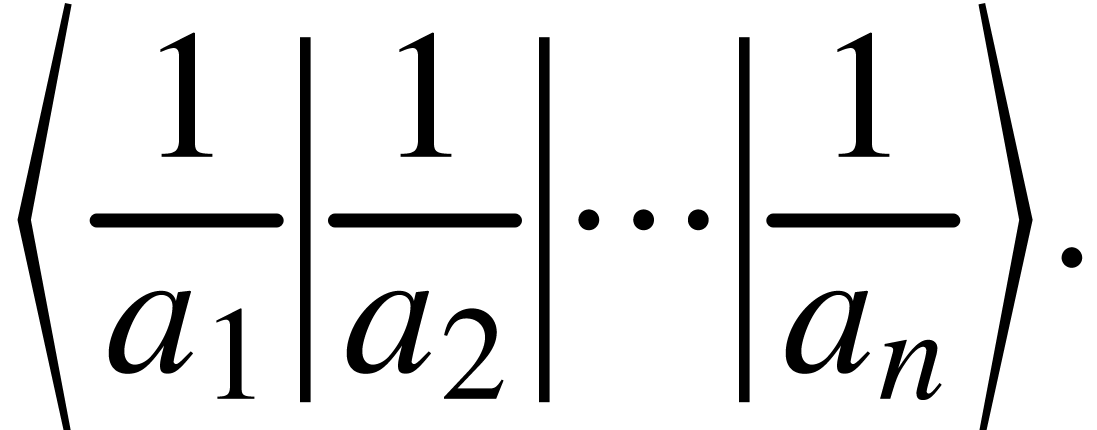
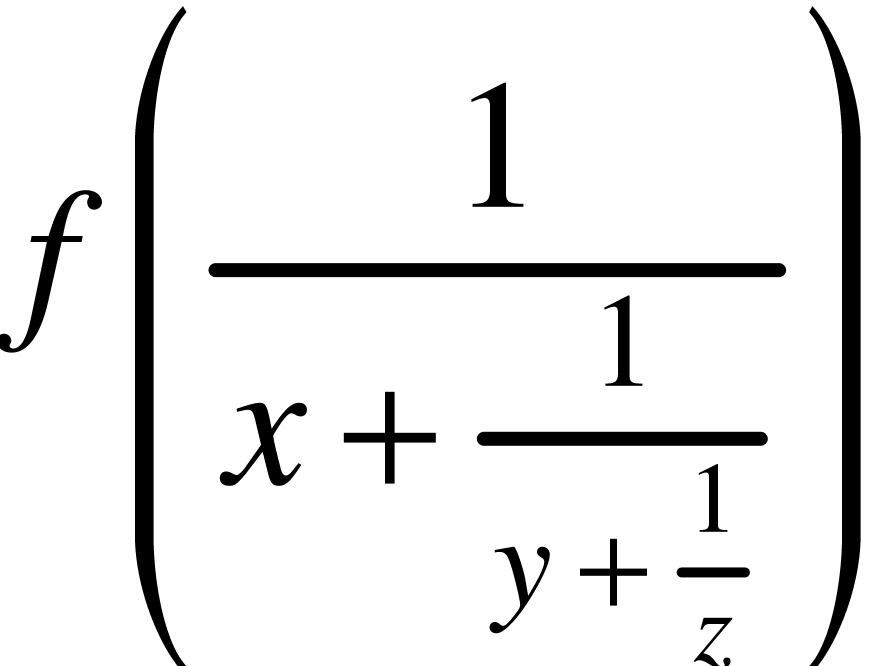
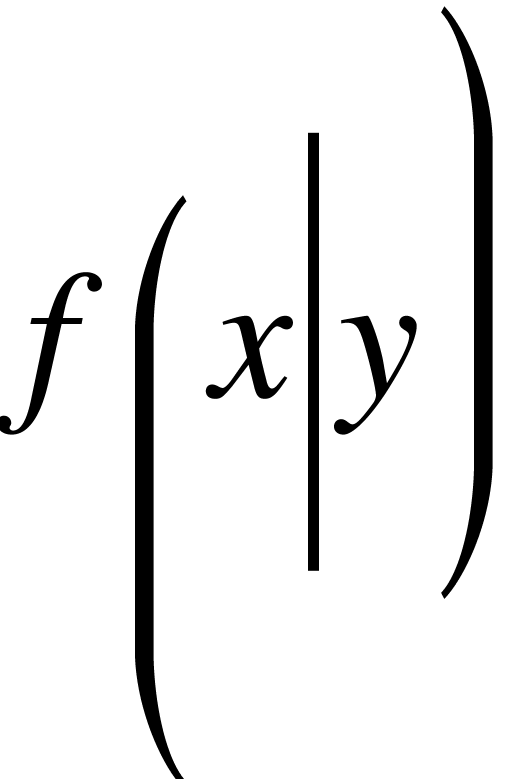
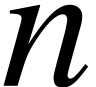 , in which case the
, in which case the 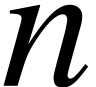 -th available size for the delimiter is taken. For
instance,
-th available size for the delimiter is taken. For
instance,
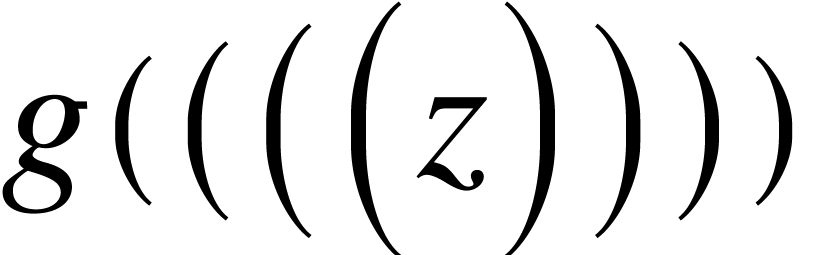
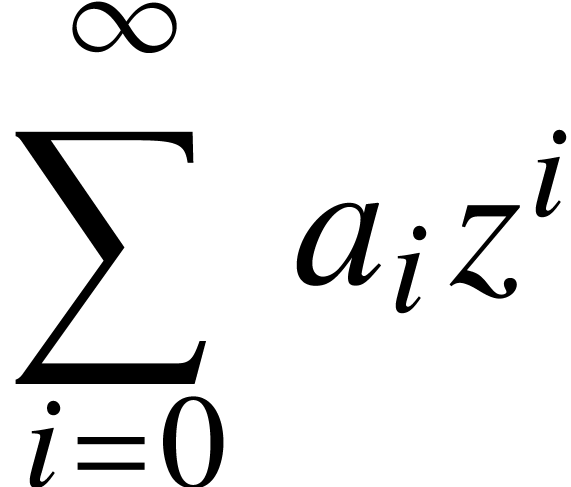
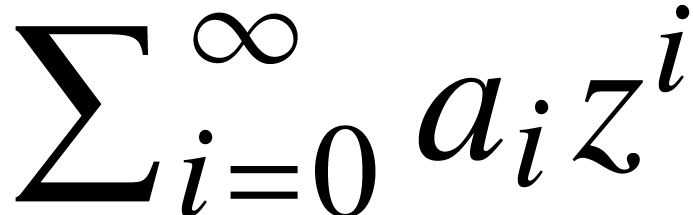 . The user may use → to override the current
settings.
. The user may use → to override the current
settings.
 . In display
style, the numerator num and denominator
den are rendered in the normal size, but
display style is turned of when typesetting num
and den. When the display style is turned
of, then the arguments are rendered in script size. For instance, the
content
. In display
style, the numerator num and denominator
den are rendered in the normal size, but
display style is turned of when typesetting num
and den. When the display style is turned
of, then the arguments are rendered in script size. For instance, the
content
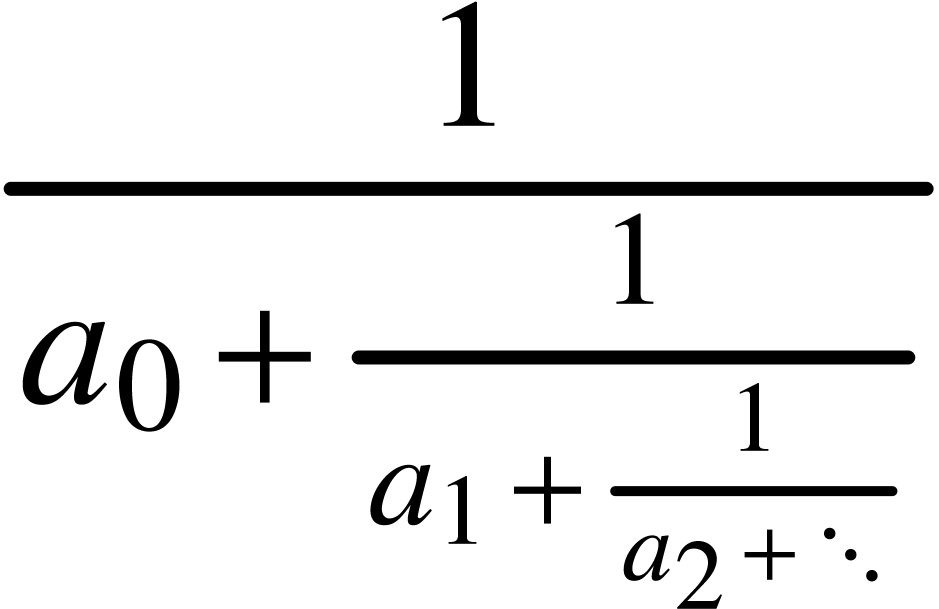
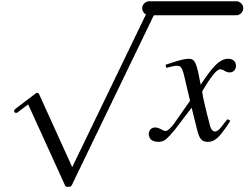 or n-th
roots like
or n-th
roots like 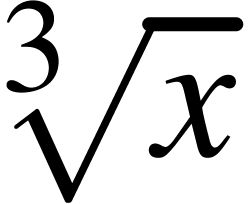 . The root
symbol is automatically sized so as to encapsulate the content:
. The root
symbol is automatically sized so as to encapsulate the content:
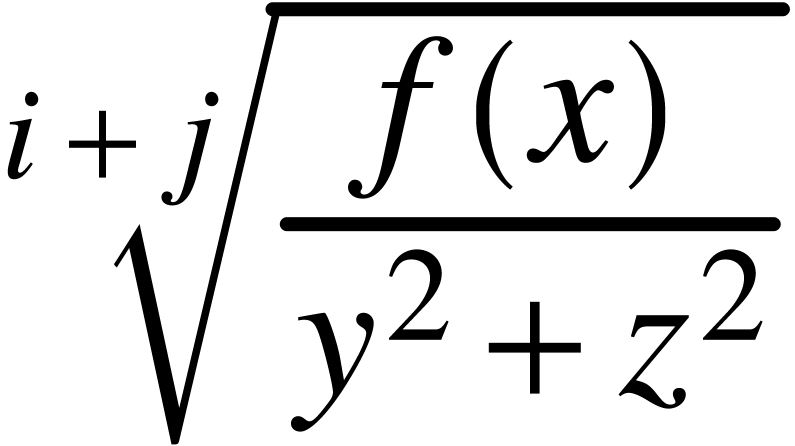
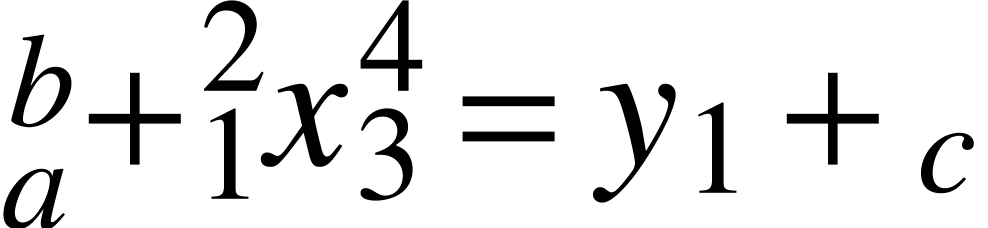
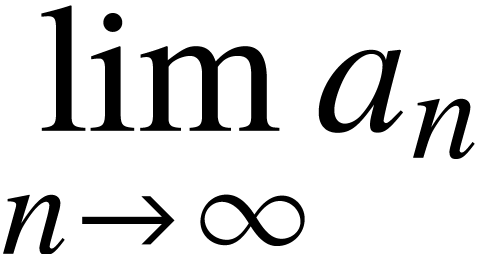
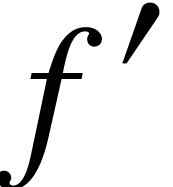 and you press backspace, then the prime is removed. If
you are behind
and you press backspace, then the prime is removed. If
you are behind 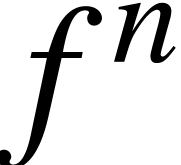 and you press backspace several
times, then you first enter the superscript, next remove
and you press backspace several
times, then you first enter the superscript, next remove 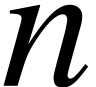 and finally remove the superscript. Notice also that
prime-symbols is necessarily a string of
concatenated prime symbols. For instance,
and finally remove the superscript. Notice also that
prime-symbols is necessarily a string of
concatenated prime symbols. For instance, 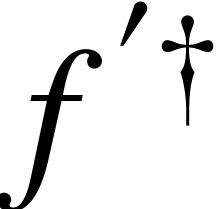 is
represented by f<rprime|'†>.
is
represented by f<rprime|'†>.
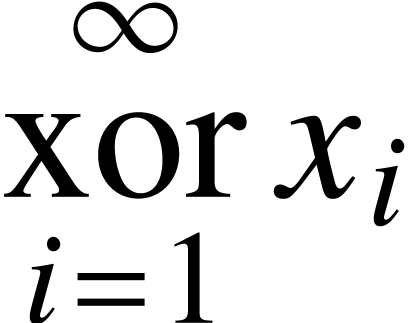
 corresponds to the markup <wide|x+y|¯>.
corresponds to the markup <wide|x+y|¯>.
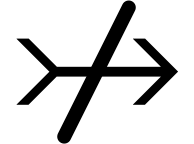 or
or  .
.
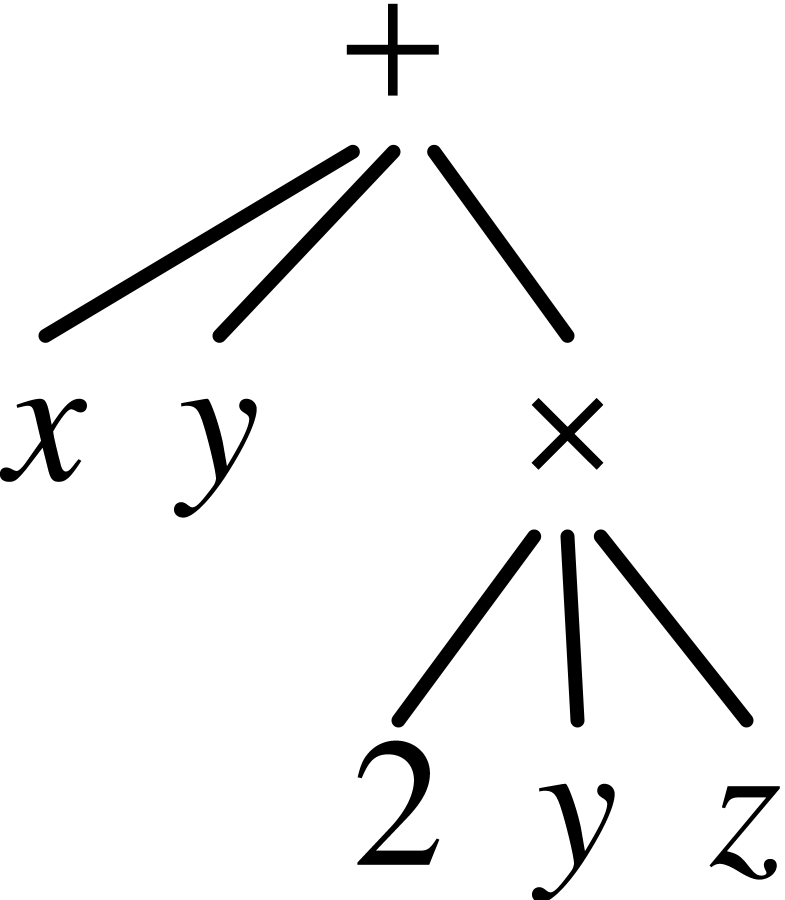
 character, which is
needed for the positioning of scripts. All the remaining
parameters are actually computed as a function of yx.
character, which is
needed for the positioning of scripts. All the remaining
parameters are actually computed as a function of yx.

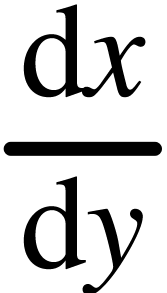 or in display style and
have different variants (standard frac, display dfrac, small inline tfrac, continued cfrac and slashed frac*). For example
or in display style and
have different variants (standard frac, display dfrac, small inline tfrac, continued cfrac and slashed frac*). For example
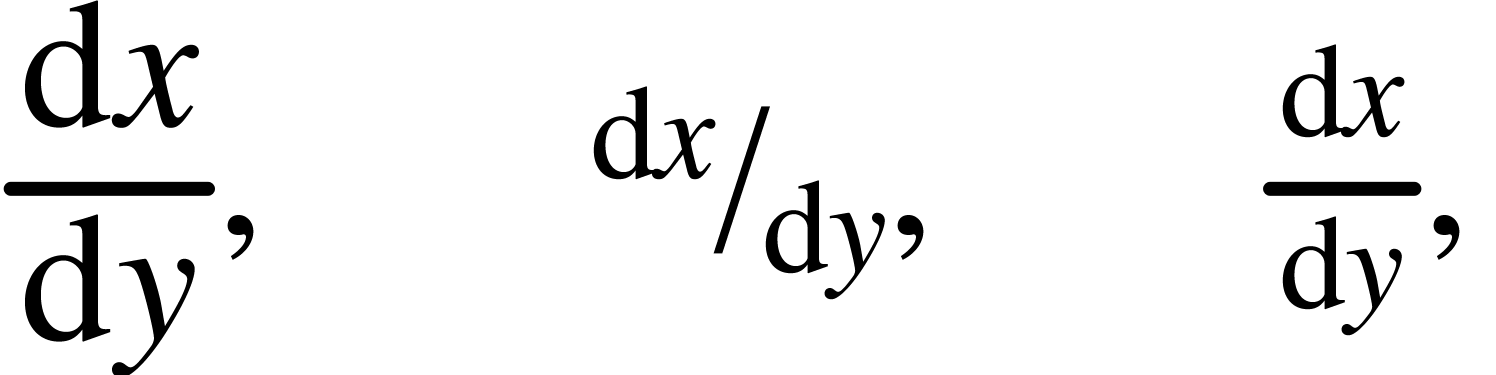
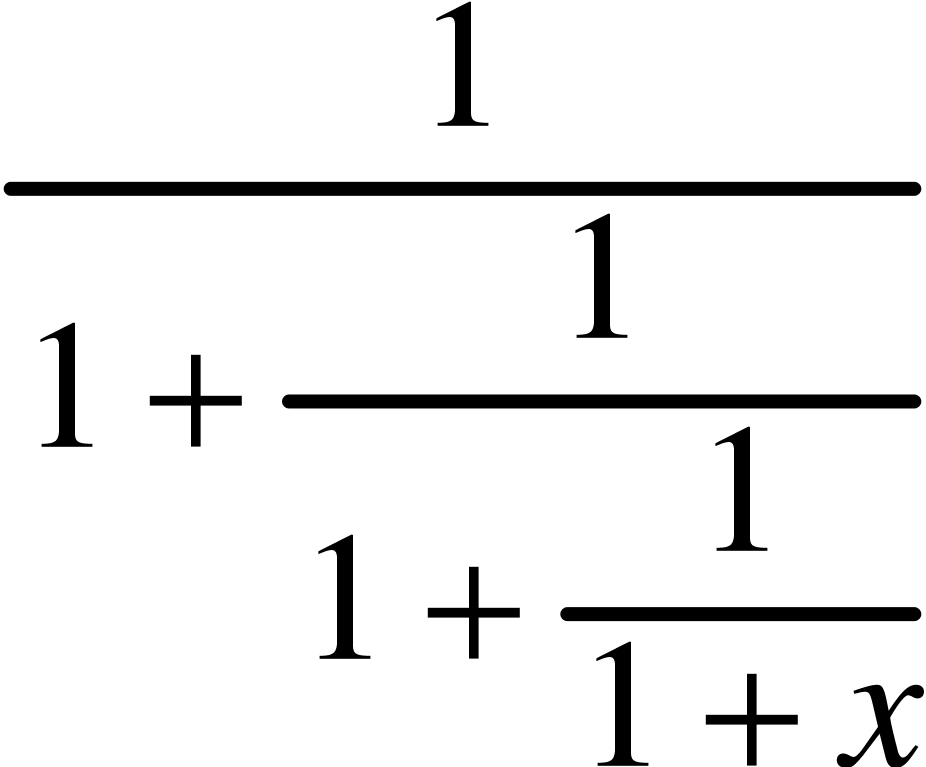
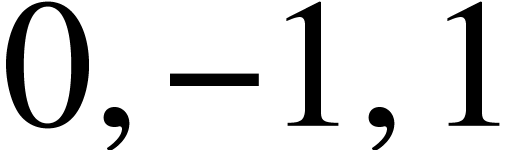 depending on where we are in the typesetting of
fractions. This is used in the finalization routines. [Add
more?]
depending on where we are in the typesetting of
fractions. This is used in the finalization routines. [Add
more?]
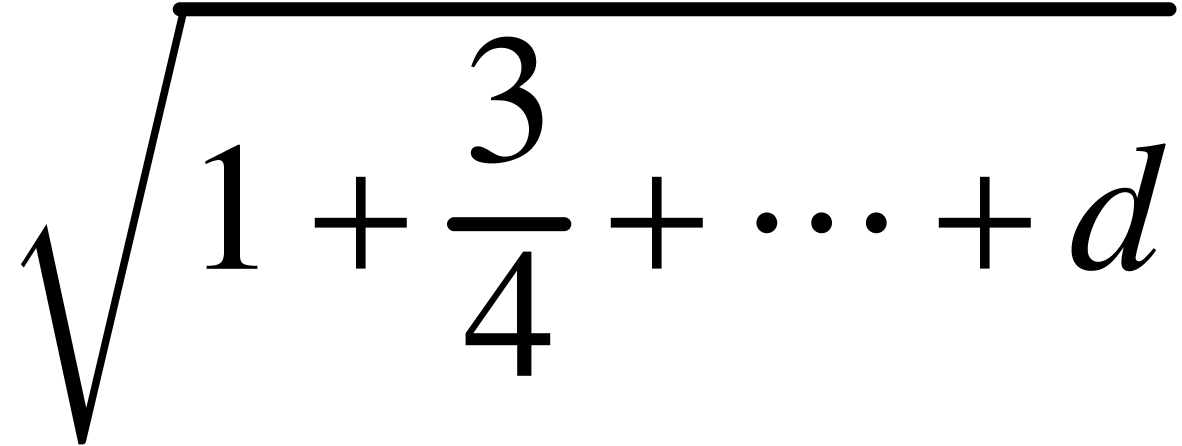
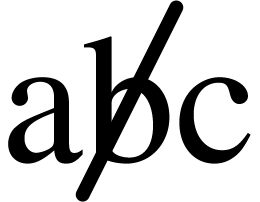
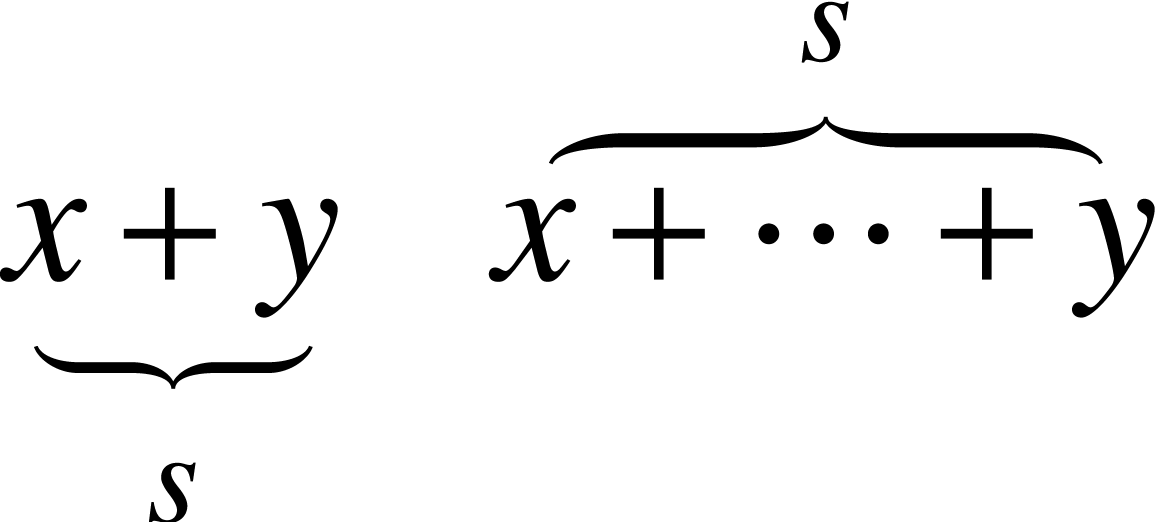
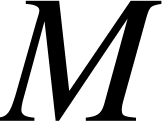 instead).
instead).
 -script
below the suggested top line.
-script
below the suggested top line.
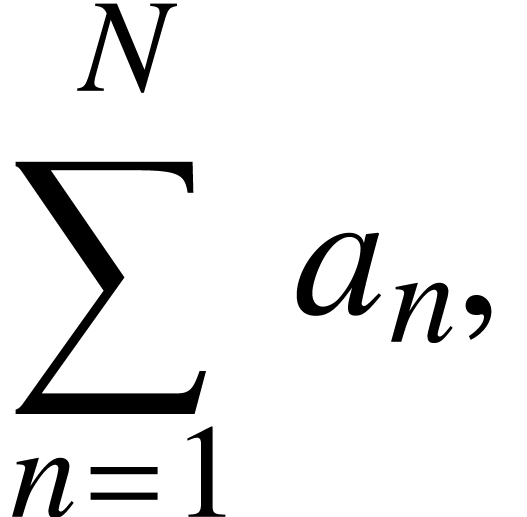
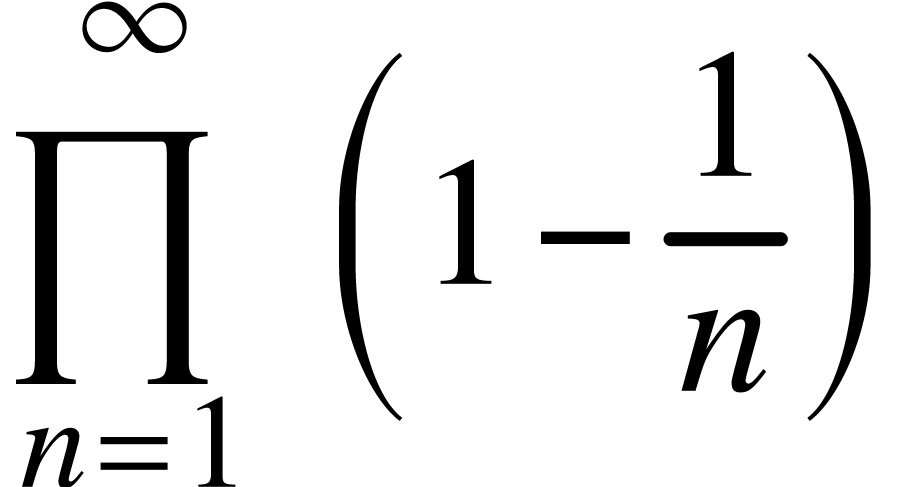
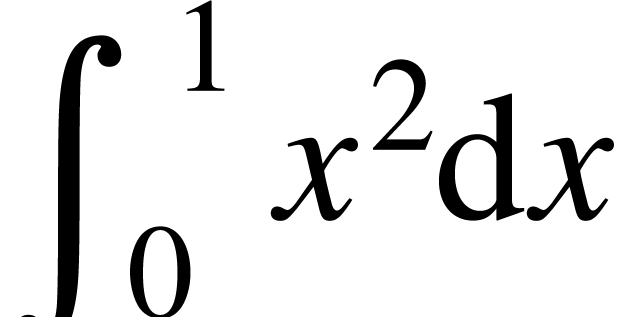
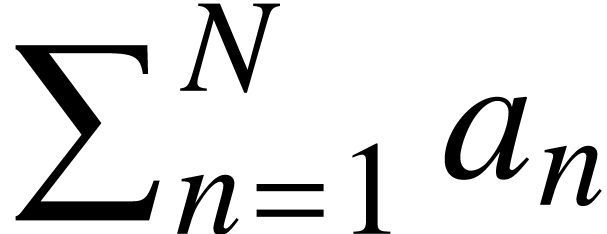 ,
, 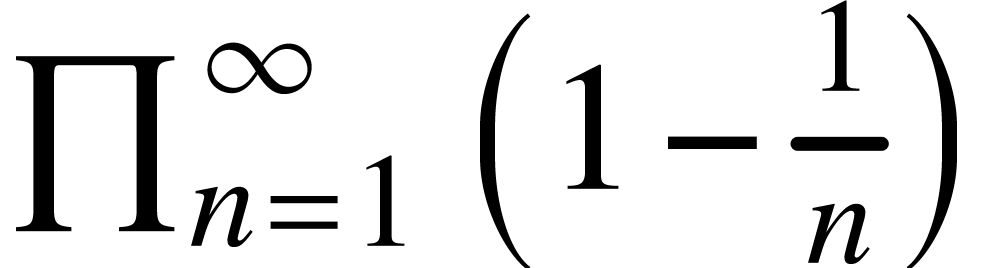 ,
, 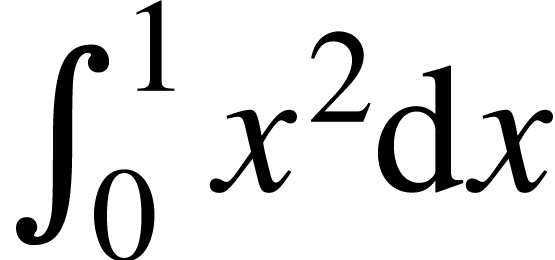 .
.
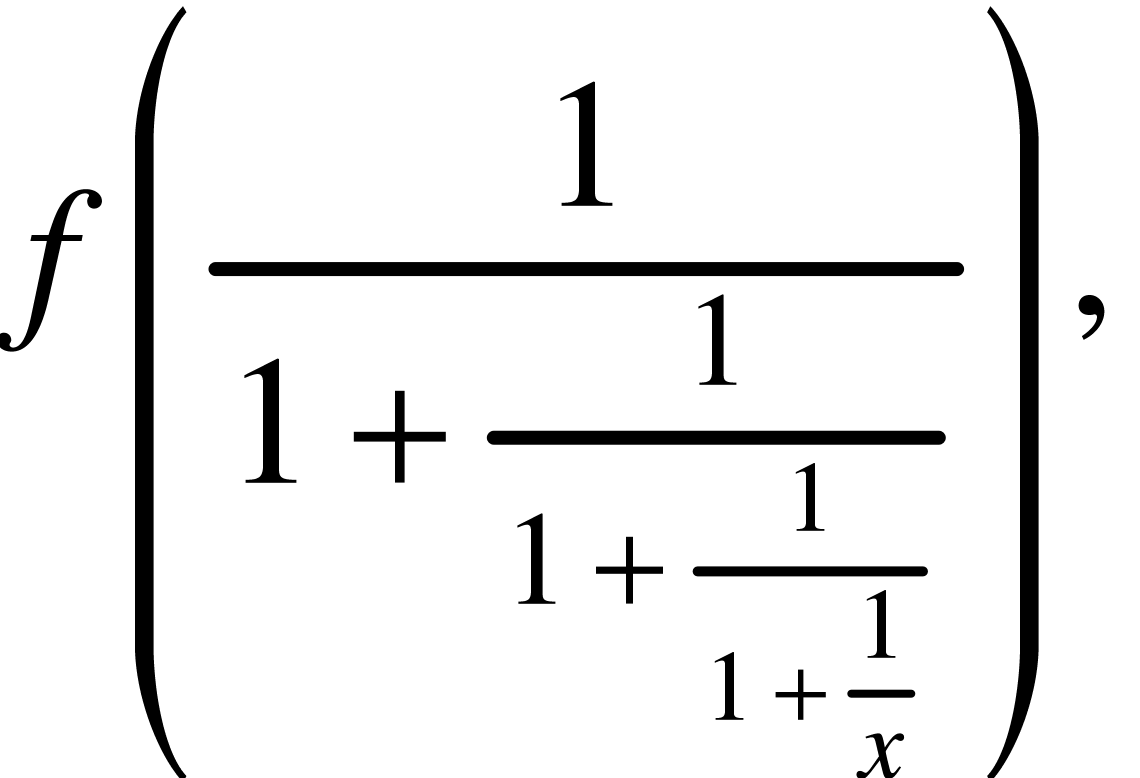
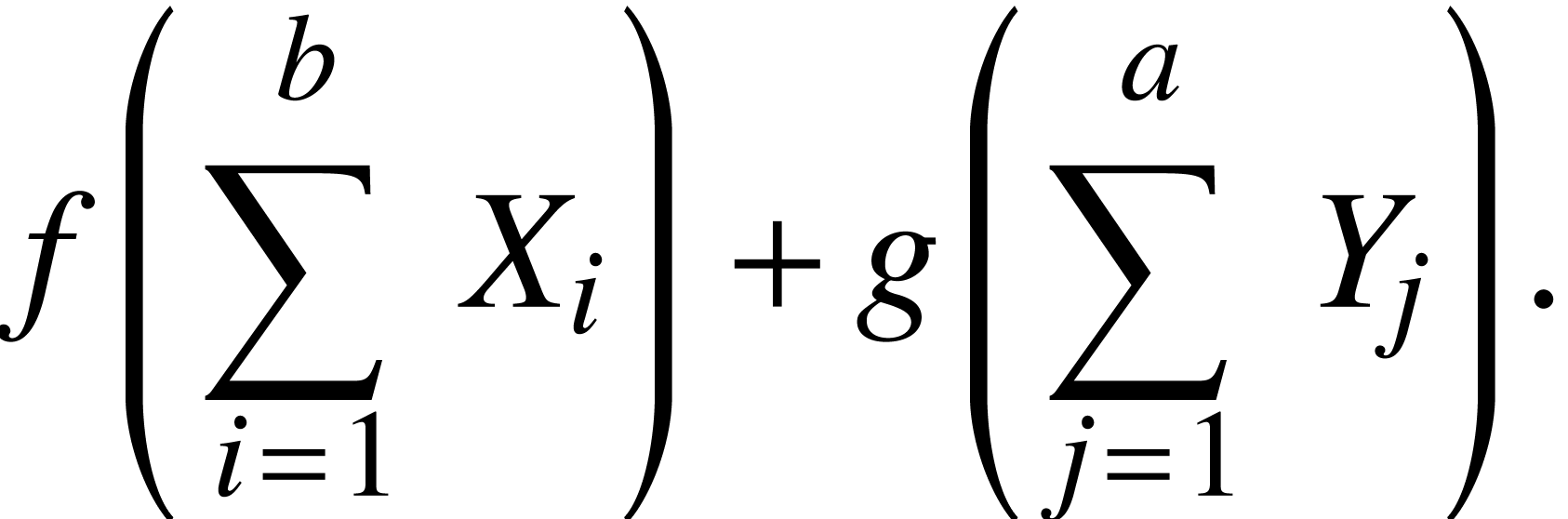
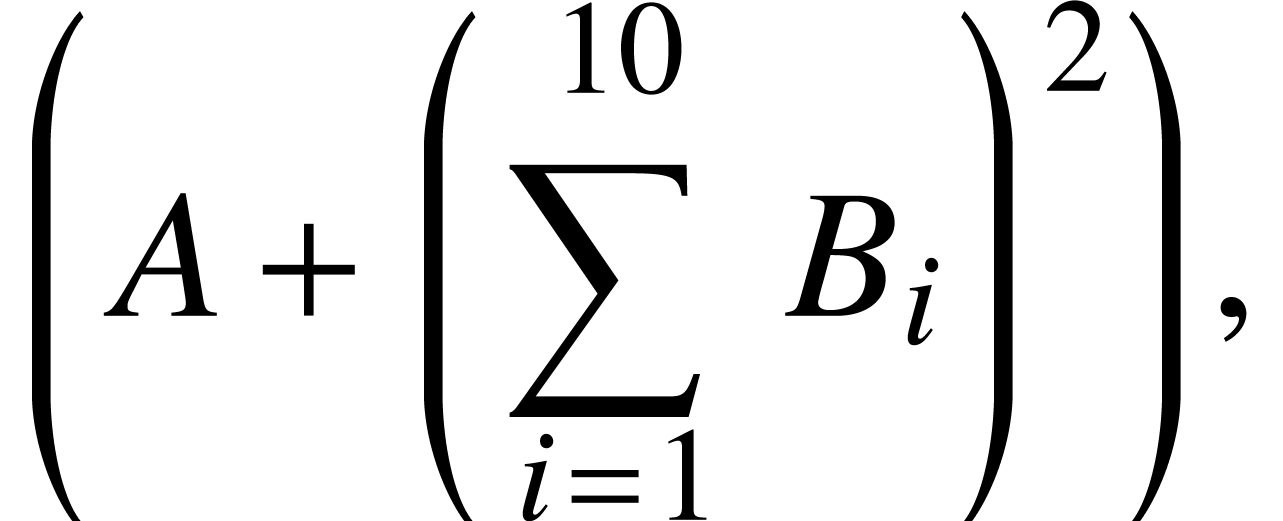
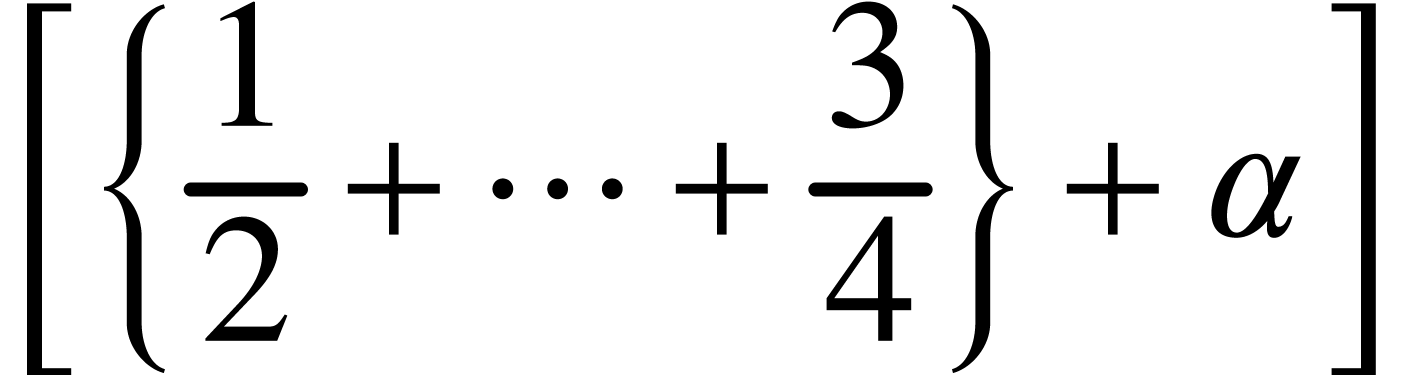
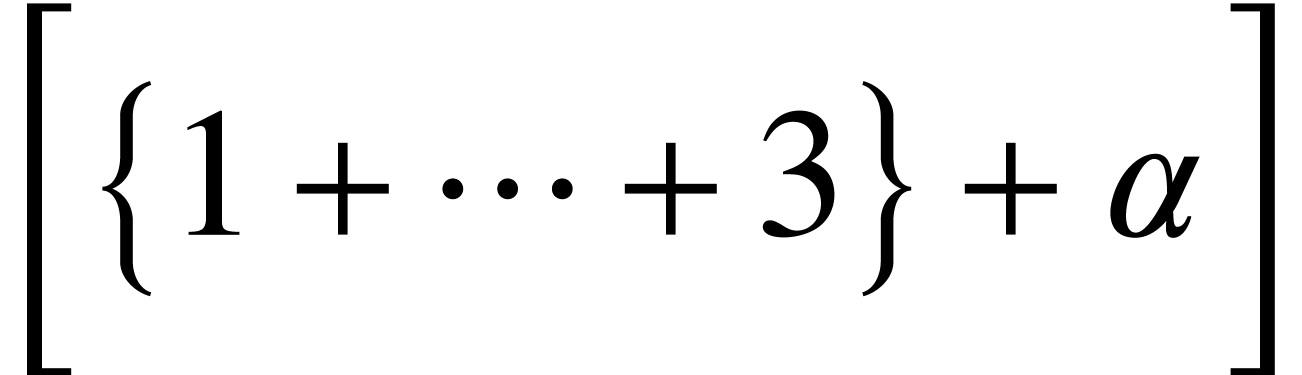
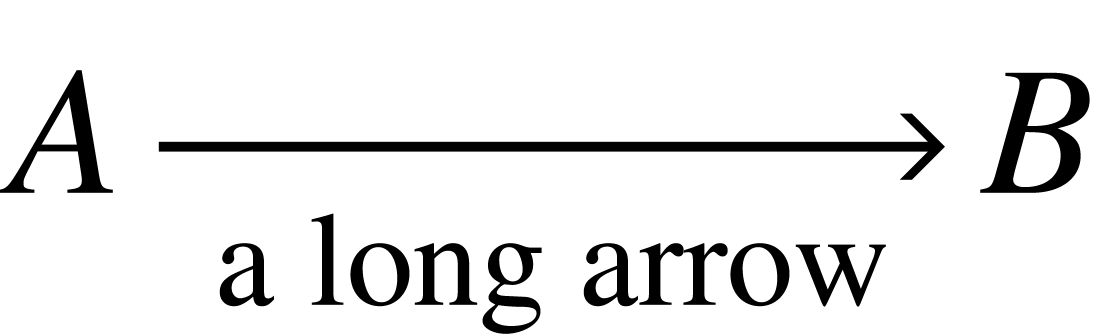

.png)



![How Much Lego Is Too Much? [video]](https://www.youtube.com/img/desktop/supported_browsers/firefox.png)

