Navigating Mars with Rust: Developing an Autonomous Pathfinding Rover

As AdaCore’s Product Manager for Rust, I wanted to build upon the innovative work my colleagues achieved with Ada and SPARK-based Mars rovers by exploring an idea: Let’s develop a pathfinding algorithm and navigational re-routing system in Rust for the rover.

In this post, we’ll demonstrate Rust's capability through the development of an autonomous navigational re-routing system. The goal is to calculate and adapt paths for a simulated autonomous rover, enabling it to effectively navigate around unexpected obstacles, leveraging a dynamic pathfinding algorithm. We’ll aim to show:

• The selected pathfinding algorithm.

• Its ability to navigate complex and changing environments in real time, and

• How details of the Rust language help us implement the algorithm safely and efficiently.

To find more information about previous Rover & Rust project implementations, please visit these blog posts:

1. Building a Virtual Mars Rover with SPARK and Rust

2. Let’s Write A Safety Monitor For A Mars Rover!

3. Adding Ada to Rust

Choosing A Best-Fit Pathfinding Algorithm

Choosing an appropriate pathfinding algorithm for our project was not easy: there are many pathfinding algorithms that have been designed over the past decades. Through my initial research, I was able to narrow numerous strategies down to three options:

• A*: Reliable and efficient, ideal for planning initial paths in known environments.

• D* Lite: Excellent for dynamically recalculating paths in response to new obstacles.

• Field D*: Offers sophisticated trajectory adjustments suitable for continuous obstacle avoidance scenarios - Used by NASA to path-find for the Mars Rovers.

For our first approach, we would need to think forward into what environment we would ultimately like to scale into.

All three algorithms show merit, however A* does not rise to the complexities of re-routing in changing environments. Although Field D* would be a fun algorithm to implement, it is significantly more complex and computationally hungry than what our project needs.

So, D* Lite is the pathfinding approach we’ll move forward with — this is ideal for our project due to its continuous cost recalculation in a grid-like environment.

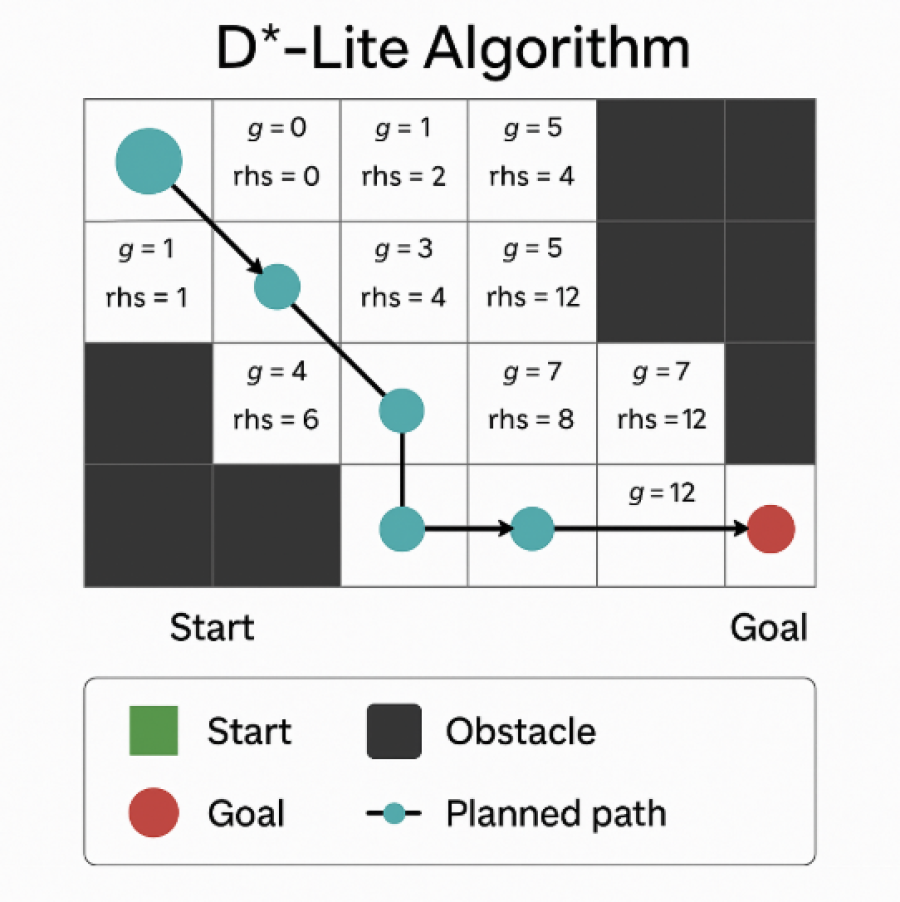
D*-Lite

The D*-Lite algorithm (short for Dynamic A*) uses LPA* (Lifelong Planning A*) to mimic D*; that is, D*-Lite uses LPA* to find the new best path for a unit as it moves along the initial best path, recalculating its path as the map or the immediately observable environment changes. D*-Lite is considered much simpler than D*, and since it always runs at least as fast as D*, it has completely replaced D* in practice.

D*-Lite works for us because it is constrained to a discrete graph where it incrementally breaks a continuous space into chunks (A* is notably non-incremental). D*-Lite uses a reverse search where it computes costs backward from a goal node. When following a path, D*-Lite re-calculates changing cost information close to the perimeter of the active search front (or “visited region”), which is continuously considered as the starting point of the search (much like an autonomous Rover using sensors to read the immediate landscape ahead and make adjustments to its route).

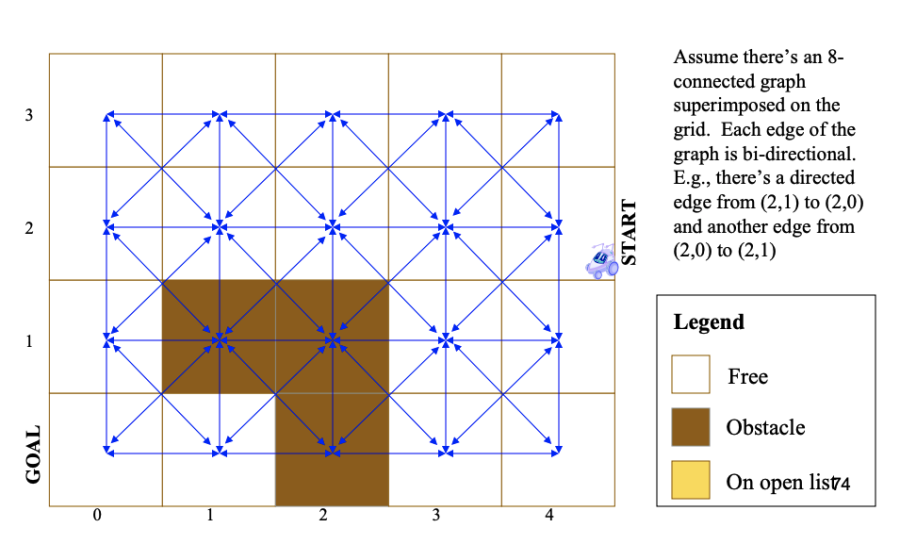
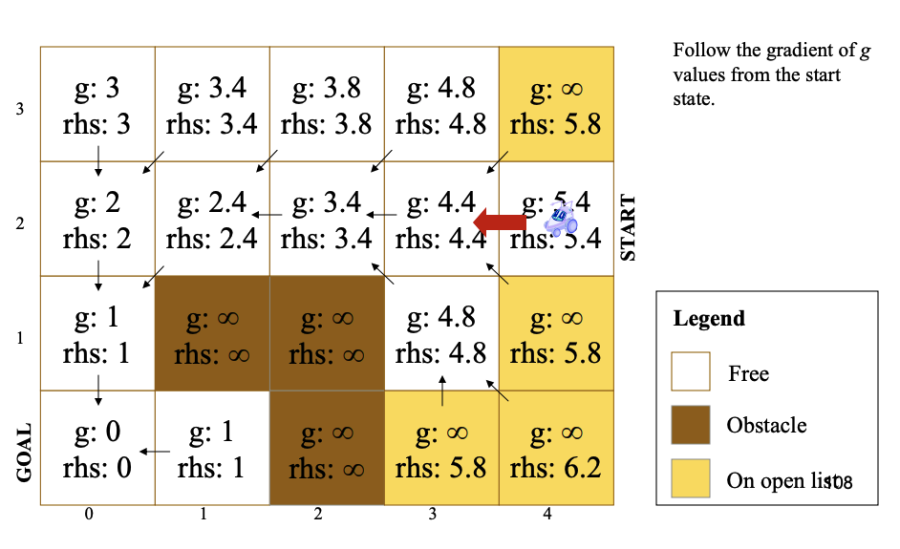
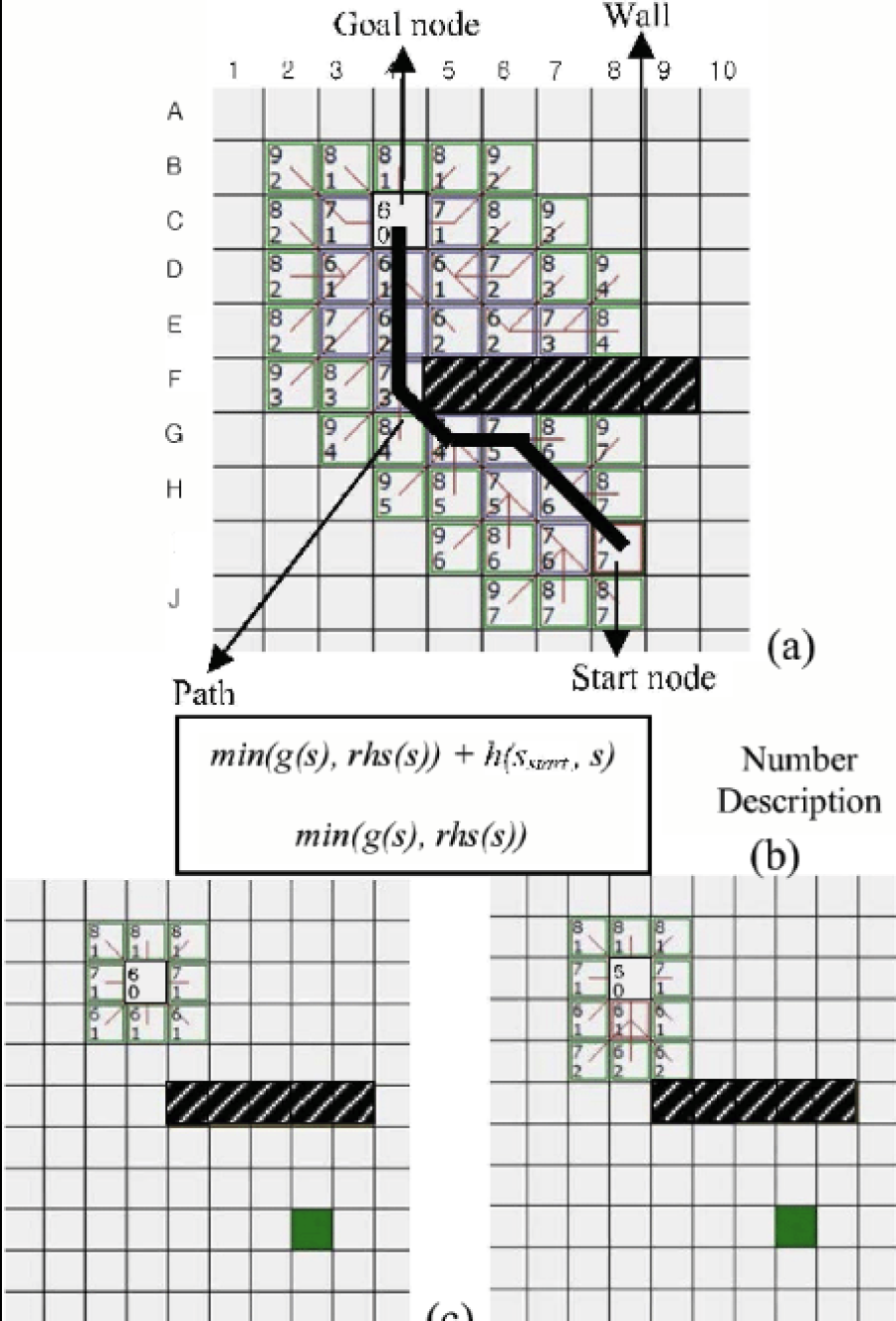
_{Diagram Source: Robotic Motion Planning: A* and D* Search}

The incremental updates of stored information help in recalculation, but due to a build-up of data, can lead to catastrophic slowdown. However, this informational bottleneck can potentially be overcome if we consider flushing stored information if the incremental update is estimated to take longer than a fresh start. Learn more about D*-Lite here.

Getting Started

First, I define a single Pathfinder trait with just two methods - compute_path(start, goal) and update_obstacle(coord, is_blocked).

— without caring whether the planner is A*, D*-Lite, or any other algorithm we might want to plug in at a later date.

At runtime, we simply swap in our DStarLite instance, call compute_path to get a Vec<Coord> route (wrapped in Option), and later invoke update_obstacle whenever the rover “sees” a new obstacle.

Under the hood, D* Lite maintains two maps of cost values (g and rhs) and an open priority queue of State objects keyed by a two‐element tuple. An incremental repair loop (compute_shortest_path) updates only the affected region of the graph. Our approach here emphasizes Rust’s zero-cost trait dispatch and strong type guarantees, while keeping the algorithm core clean, self-contained, and easy to swap out in the project.

A note on why we make the result optional

In any realistic map, there are situations where no valid route exists — it’s possible the goal cell itself is blocked, or obstacles completely surround the starting point. By making compute_path return an Option<Vec<Coord>>, we encode that possibility directly in the type system: Some(path) means we found a route, and None means “sorry a path to the goal does not exist.” This approach is safer and clearer than a null pointer. At the call site you can then write:

Here, if let Some(...) cleanly maps the path when present and gives you an else branch to recover when it isn’t available. Compared to C’s boolean-and-pointer-outpram, or C++’s exceptions: Rust’s Option keeps control flow local, avoids panics, and makes it impossible to forget handling the “no path” case at compile time.

Type Definitions: State and Neighbors

Rust’s expressive derive macros allow us to bundle hashing, comparison and cloning into a small struct. This is markedly different from languages like C++, where you’d hand-roll comparators and hash functors. By deriving Hash, Eq, and PartialEq, our State can live in both a BinaryHeap (for priority ordering) and a HashSet (for quick membership checks) without boilerplate. The two-tuple key implements a custom min-heap ordering, and Clone + Copy ensures cheap, stack-based duplication.

D*-Lite Structure

While it may seem odd to have nonnegative values for coordinates, the planner lives on a fixed-size, strictly positive grid (Vec<Vec<bool>> indexed by usize). This design uses strictly positive grid coordinates stored as usize values. While usize inherently prevents storing negative coordinates, arithmetic operations on usize can still underflow (wrap-around). To ensure safety, we explicitly convert coordinates to signed integers (i32) for calculations and perform explicit bounds checks (nx_i >= 0 && nx_i < width as i32) before indexing into the grid. This explicit checking prevents accidental underflow or negative indexing, thus maintaining correctness and safety at runtime.

A fixed-size world simplifies embedded deployments on microcontrollers or smaller Single Board Computers (SBC’s), though we’d trade off the ability to grow dynamically if the environment called for it. The inclusion of both g and rhs maps, plus an open_list heap and open_set for quick membership, encapsulates all the state D*-Lite requires.

If we were implementing the algorithm in an unbounded world, we would likely need a different structure. The Pathfinder trait we have implemented would support us switching to an unbounded or dynamically growing environment as it only specifies what a planner must do (plan and replan), not how to store its world — allowing us to exchange backing structures without touching the trait itself. We would, however, need to write a new implementation using a spatial index of our choosing instead of Vec<Vec<Bool>>.

The Core Loop: compute_shortest_path

D*-Lite’s compute_shortest_path loop incrementally repairs the search tree by refining just the affected parts of the cost-to-come (g) and one-step lookahead (rhs) values, instead of rebuilding the entire search from scratch after each obstacle. It does this by maintaining an open list of nodes whose priorities changed and processing only those. During each iteration, it handles “overconsistent” nodes (where g > rhs) by setting g = rhs and updating predecessors, or “underconsistent” nodes (where g < rhs) by resetting g to infinity and re-propagating lookahead values outward. This targeted approach lets the planner adapt to new obstacles with far less work than a full A* replan, preserving most of the previous search effort.

Guarded Loop - Rather than a plain while !open_list.is_empty(), Rust’s while let pulls both the condition check and the first element into one succinct pattern.

This effectively says “as long as there is a top element, bind it to top and run the body.” We use .peek().cloned() so that we inspect the current minimum-priority node without popping it immediately. This gives us a chance to compare its old priority (old_key) to a freshly computed one (new_key), where we only pop and process it if they match. This pattern ensures we don’t inadvertently drop elements and keeps the code clear about exactly when removals happen.

Graceful Defaults with unwrap_or(&INF) - In D*-Lite we maintain two per-node maps: g and rhs. Early in the search, many cells haven’t been touched yet, so they won’t appear in those maps. By using:

A High Level Wrapper with compute_path - The compute_path method serves as a single entry point that handles any changes to the start or goal node, runs the incremental repair loop, checks for reachability, and then reconstructs the final route. In one call, it reseeds the search if the start or goal have moved by bumping the heuristic modifier and reinitializing to goal’s lookahead, invokes compute_shortest_path to incrementally propagate cost updates, and returns None if the start remains unreachable. Otherwise, it walks through greedy successors (using g + edge_cost) to build and return the Vec<Coord> path.

This high-level wrapper cleanly separates the “bookkeeping” work of start/goal node management from the core repair logic below:

A Resulting Rust Advantage

1. Rust's Borrow Checker

Rust’s borrow checker ensures safe memory usage, making it easier to manage concurrent data updates and avoid data races. This feature is particularly beneficial when parallelizing incremental algorithms like D*-Lite, enabling safe and efficient recalculations in response to dynamic environmental updates.

• Memory Efficiency:
  By precisely controlling data access and ensuring references are clearly marked as either mutable or immutable, we prevent unexpected memory behaviors and reduce overhead. The borrow checker makes it straightforward to efficiently update or discard stored incremental cost information when recalculating paths, as demonstrated below.

• Incremental Update Management:
  Rust allows explicit control over when data is mutated or dropped. For our D*-Lite implementation, this enables us to quickly flush outdated cost information if recalculating incrementally becomes computationally heavier than starting afresh.

2. Trait System & Zero-Cost Abstractions

Rust’s trait system promotes code modularity, clarity and reusability—particularly advantageous for algorithmic efficiency. The trait system also helps us plug in additional algorithms in the future if we so choose.

• Abstraction and Flexibility:
  Traits enable us to define clear interfaces for different components, such as pathfinding logic, sensor input handling, and cost evaluation strategies. This modular approach simplifies swapping out or improving components independently, ensuring optimal performance as incremental updates occur.

• Algorithmic Optimization:
  By implementing D*-Lite through clearly defined traits (e.g. - GraphSearch, CostUpdater, ObstacleDetector), we can easily benchmark and optimize individual components, quickly identifying and mitigating potential performance bottlenecks in our incremental updates.

A note on Zero-Cost Abstractions

This topic is discussed frequently by the Rust community so, in the spirit of posterity, I believe it is worth providing some additional color as to how we benefit from it. Zero-Cost Abstractions simply means there is no runtime overhead from dynamic dispatch or virtual function tables.

• We use traits for modularity (e.g., GraphSearch, CostUpdater, ObstacleDetector), which allows us to swap or modify algorithms (or other functions) without rewriting large sections of code.
• When our Rust code utilizes traits, the compiler applies a process called monomorphization, which creates optimized, specialized versions of the code for each specific use case at compile time.

In contrast, C++ abstract functions often rely on virtual functions typically implemented through virtual tables (vtables) which incur small runtime penalties whenever a method is called. This specifically can accumulate in systems tight on compute (such as path recalc).

3. Strong Type Safety

Rust’s type safety ensures correctness at compile-time, significantly reducing runtime errors—a cornerstone for safety-critical autonomous systems.

• Error Reduction:
  Explicit types help prevent logical errors that might otherwise arise during complex incremental updates, maintaining system stability under continuous recalculation scenarios.

• Predictable Performance:
  Type annotations clearly define the computational expectations of different functions and data structures. This explicitness helps avoid unintended costly operations during incremental updates, making performance more predictable and stable.

Altogether, Rust’s ownership model, trait abstractions, and rich crate ecosystem (wasm-bindgen, web-sys, gloo::timers, serde, etc) let us build a rock-solid, high-performance, interactive pathfinding demo—and later drop that same core into an embedded PI Zero rover with confidence that we won’t encounter subtle memory or data-race bugs.

At this point, we have implemented the D*-Lite algorithm and uncovered why Rust is an excellent choice in complementing our pathfinding strategy.

Where can we take this?

• Implement a stand-alone simulation for testing and refining our implementation of D*-Lite

• Implement perception and state estimation for the Rover - the Rover can't plan a route around obstacles if it doesn't know where it or they are!

• Putting the Rover to the test - adding perception, state estimation, and pathfinding to the Rover

Follow the Project & Submit Questions

If you're interested in this project I encourage you to stay engaged and follow its progress on the ScoutNav GitHub Repository.

Please leave your questions in the comment section below and I’ll plan to address them in our upcoming live webinar "Navigating Mars with Rust: Putting Rust to the Test with the M.A.R.S. Rover," scheduled for July 8th.

See you all there!