Plasmonic metasurfaces with unclonable stochastic scattering for authentication

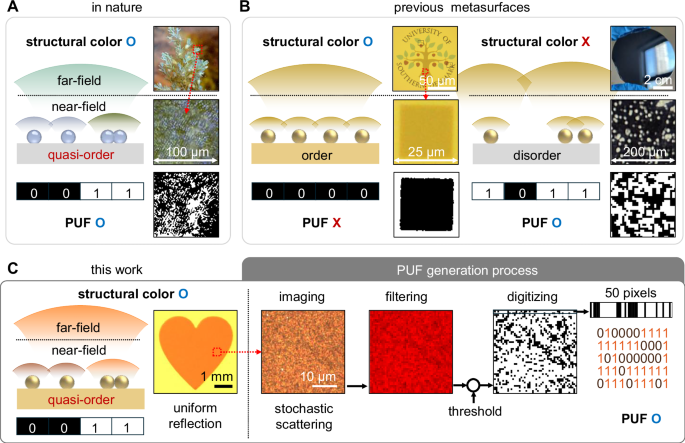
Since the pioneering observations of Isaac Newton¹ and Robert Hooke², structural coloration in nature has captivated attention for its ability to produce vivid, uniform colors that are both visually striking and functionally critical, serving roles in camouflage, signaling, and species recognition³. These remarkable optical effects arise from the precise arrangement of micro- and nanostructures, which modulate light-matter interactions to generate intense reflective colors⁴. However, embedded within this structural precision is an inherent randomness, caused by factors such as cell division^5,6 and irregular growth patterns^7,8, leading to a localized, imperfect order known as ‘quasi-order’^9,10. This intricate balance between order and randomness is a defining feature of diverse biological systems, including butterfly wings¹¹, algae leaves¹², insect exoskeletons^13,14, and fruit peels (Fig. S1)¹⁵. These naturally occurring quasi-ordered structures exhibit a dual optical function: (1) maintaining uniform far-field reflective colors, essential for visual signaling and environmental camouflage, while (2) generating unique, stochastic near-field optical responses, akin to human fingerprints (Fig. 1A).

Fig. 1: Concept of unclonable stochastic scattering in structural coloration.

A Far-field uniform structural color in nature with near-field stochastic colors driven by their intrinsic structural quasi-order. The right panel shows one example, brown algae’s stochastic coloration (middle) and associated optical PUF we generated (bottom)¹². Reprinted with permission from AAAS (Copyright 2018, AAAS). B Previous plasmonic metasurfaces for uniformly ordered structures for both far- and near-field uniform color (left) and disordered structures for both far- and near-field stochastic colors (right). The left and right insets are respectively reprinted with permission from American Chemical Society (Copyright ACS Publications)¹⁷ and from Springer Nature (Copyright Springer Nature)²⁷. C Our plasmonic metasurface with quasi-ordered structures for far-field uniform structural color (left) with near-field stochastic colors for PUF generation (right panels).

Despite the ubiquity of quasi-order in nature, replicating this balance in artificial systems has proven to be a significant challenge. Conventional photonic metasurfaces typically prioritize either ordered architectures for uniform coloration (left panel of Fig. 1B) or disordered configurations to achieve stochastic optical responses (right panel of Fig. 1B), but rarely achieve both simultaneously. For instance, plasmonic metasurfaces, composed of metallic nanostructures arranged in regular arrays, can produce vivid structural colors across the visible spectrum with high spatial resolution, often at sub-500 nm scales^{16,17,18,19,20}. These metasurfaces, fabricated using techniques such as laser printing¹⁷, electron beam lithography^21,22, and two-photon lithography²³, excel in applications requiring aesthetic uniformity, but lack the inherent randomness required for secure authentication (left panel of Fig. 1B). Conversely, disordered photonic metasurfaces, fabricated through direct physical^24,25,26 and chemical growth^27,28, or controlled coating methods²⁹, can generate stochastic optical responses beneficial for distinct identification and security applications (right panel of Fig. 1B)²⁷. These randomly formed nanostructures act as optical physically unclonable functions (PUFs), where their intrinsic physical randomness enables the generation of unique, tamper-resistant security keys—akin to biological fingerprints³⁰. Unlike electrical PUFs, which require direct contact-based readout and consume power³¹, optical PUFs enable contactless, visually intuitive authentication, making them particularly suited for high-security applications in textiles, pharmaceuticals, and luxury goods³². However, the uncontrolled randomness of disordered nanostructures often comes at the expense of far-field color uniformity, limiting their practical application in security labels that also require aesthetic or camouflage function^30,33,34,35.

Recent efforts to bridge this trade-off have focused on 3D photonic crystals with controlled defects^36,37,38, which, like their biological counterparts, use periodic nanostructures to generate uniform far-field structural colors while leveraging random lattice defects for stochastic near-field variations. However, photonic crystal-based PUFs face a fundamental constraint: the same periodic nanostructure determines both the far-field color and the near-field stochasticity, leading to inherent coupling between color tuning and randomness. For instance, in a typical SiO₂ sphere-based photonic crystal, shifting the far-field color from red to blue requires reducing the lattice spacing from 225 to 155 nm³⁹. This alteration affects not only the coloration but also the stochastic features, making it difficult to maintain consistent authentication properties (Fig. S2). As a result, the intrinsic dependence between periodic order and randomness constrains the flexibility of photonic crystal-based PUFs for applications requiring both precise color control and secure authentication.

To address this challenge, we here present quasi-ordered plasmonic metasurfaces that fully decouple the mechanisms governing far-field coloration and near-field stochasticity (Fig. 1C). Using electrostatic self-assembly, we swiftly and uniformly transfer plasmonic nanoparticles onto a metallic mirror patterned with dielectric structures, achieving quasi-order across the entire surface within a minute. In this system, the uniform far-field reflective color is independently tuned by the dielectric gap thickness, while the stochastic near-field scattering patterns emerge from the random oligomeric and monomeric nanoparticle distributions. This decoupling allows precise tuning of the far-field color across the entire visible spectrum without compromising the stochastic nature of the scattering PUF. The resulting metasurfaces demonstrate remarkable uniformity, uniqueness, and stability, making them highly suitable for secure authentication technologies. To illustrate their practical potential, we integrate these metasurfaces into everyday security applications, such as ID cards and QR codes, showcasing their scalability for anti-counterfeiting measures that combine aesthetics with hidden authentication.

Concept of unclonable stochastic scattering with plasmonic metasurfaces

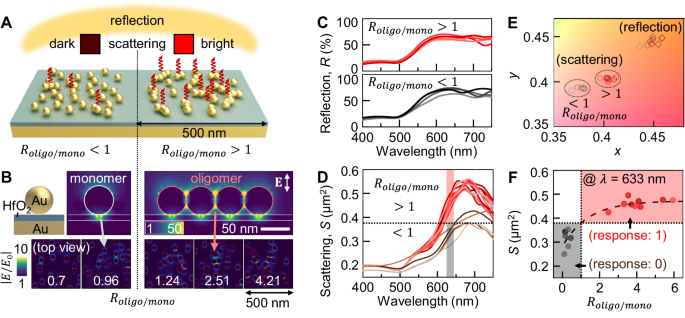
Our design draws inspiration from the naturally occurring quasi-order in micro/nanostructures observed in animal feathers and plant leaves, which create intrinsic stochastic near-field fingerprints while maintaining far-field uniform structural colors (Fig. S1)^{11,12,13,14,15}. To mimic this effect artificially, we begin with a numerical modeling of a plasmonic metasurface comprising gold nanoparticles (Au NPs) positioned just above a metallic mirror, separated by a dielectric gap (Fig. 2A). For instance, a 50 nm single Au NP placed on an Au mirror, referred to as a ‘monomer’, exhibits behavior akin to a dimer pair of two Au NPs, resulting in strong optical near-field coupling within the gap, often termed a ‘hotspot’ (top-left panel of Fig. 2B). This hotspot induces coupled resonant color, enabling the Au NP to function as a fundamental unit for structural coloration, such as a reflection peak at 621 nm when spaced by 20 nm HfO₂ layer (Fig. 2C)⁴⁰. Consequently, when Au NPs cover the entire mirror surface, the uniform far-field reflective color arises from the consistent surface coverage of the Au NPs across the mirror, effectively behaving like a metallic layer and thus acting as Fabry-Perot etalons⁴¹.

Fig. 2: Theoretical design of plasmonic metasurface.

A Schematic of differential scattering colors due to R_oligo/mono, the ratio between the forms of oligomers (aggregated Au NPs) and monomers (isolated Au NPs) at the given number density while exhibiting uniform reflective color regardless of the ratio. B Optical near-field enhancements of the monomer (top-left) and oligomer (top-right), and their random distributions as a function of R_oligo/mono at the given number density (NP number: 31, area: 500 × 500 nm, bottom panel). C Associated reflection spectra, D scattering spectra, E color gamut plots in CIE 1931 chromaticity, and F scattering intensity at \({\lambda }\) = 633 nm vs. R_oligo/mono.

Meanwhile, despite this consistent surface coverage, random local arrangements of Au NPs, termed ‘oligomers’, arise due to varying numbers and orientations of Au NPs, except for a few cases involving nanolithography or nanopatterning^42,43. These quasi-ordered oligomers generate additional optical near-field coupling within the gaps between Au NPs (top-right panel of Fig. 2B), resulting in scattering intensities that are 1.5 times stronger than those generated by monomers (Fig. 2D). Interestingly, when defining \({R}_{{oligo}/{mono}}\), the ratio of oligomers to monomers within a given surface area (500 × 500 nm for simulation) while maintaining an overall surface coverage of 24%, and sweeping this ratio from 0.7 to 4.2 (bottom panel of Fig. 2B), the scattering color at the wavelength of 633 nm (for red color) clearly bifurcates into two regimes, i.e., dark and bright scatterings when \({R}_{{oligo}/{mono}} < 1\) and \( > 1\) respectively, all while maintaining consistent reflective color irrespective of the ratio (Fig. 2E). These distinct scattering behaviors enable digitization of the signals into binary values, ‘0’ and ‘1’ based on whether the ratio is less than or greater than 1 (Fig. 2F). Moreover, this approach generates stochastic scattering patterns with high spatial resolution (e.g., Fig. 3), making it highly suitable for scattering-based physically unclonable function applications.

Fabrication of plasmonic metasurfaces

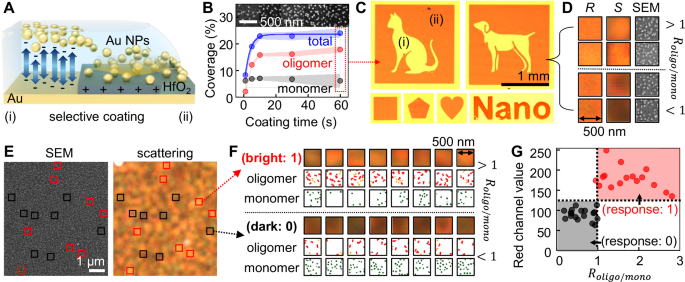
The key to enabling quasi-order in the plasmonic metasurface involves the self-assembly of colloidal Au NPs into the monolayer, essentially causing the various structural forms of Au NPs (Fig. 3A)⁴⁴. Our approach thus utilizes an electrostatic assembly method where chemically synthesized colloidal Au NPs (ca. 50 nm) are drop-cast onto an Au film patterned with HfO₂ (Fig. 3B, see “Methods” and Fig. S3 for details). Unlike traditional electrostatic assembly, we employ a recently developed technique⁴⁵, involving the use of protons to dissolve hydroxyl groups on the surface, thereby exposing the intrinsic surface charges, i.e., negative for Au film and positive for HfO₂ patterns. This approach enables the rapid and selective assembly of negatively charged Au NPs onto the positively charged HfO₂ patterns within seconds, while the Au film remains uncoated due to electrostatic repulsion⁴⁶, Fig. 3C. Since this assembly follows the adsorption kinetics of Langmuir isotherms, the surface coverage of Au NPs can be effectively controlled by the assembly time⁴⁷. For example, the surface coverage can be tuned from 8 to 24% by varying the assembly duration from 1 to 60 s (Fig. 3B, see “Methods” for image analysis)⁴⁸.

Fig. 3: Fabrication of plasmonic metasurfaces.

A Selective Au NPs transfer via electrostatic nanoparticle assembly. B Surface coverages of the total Au NPs at the given area of 2 × 2 μm (blue) and their forms of oligomer (red) and monomer (black) vs. coating time (inset: associated SEM images). C Plasmonic metasurfaces with various patterns and D their corresponding reflection, scattering, and SEM images at different R_oligo/mono. E SEM and scattering images of the plasmonic metasurface with randomly selected bright (red box) and dark areas (black box, each area: 500 × 500 nm). F Their corresponding scattering colors (top) and numbers of oligomer (middle) and monomer (bottom) analyzed and extracted from the SEM image. G Associated red channel value vs. R_oligo/mono.

We deliberately select the surface coverage of 24% for the Au NPs, as this not only achieves nearly half of the theoretical maximum surface coverage for quasi-ordered spheres (54%)⁴⁹, an optimal condition for binary operation, but also yields a vivid and uniform reflective color across the entire metasurface (Fig. 3C). Crucially, at this surface coverage, over 70% of Au NPs form oligomers, leading to bright scattering, which we assign as the response ‘1’ in the binary operation (Fig. 3D). To experimentally validate this, we randomly select 18 areas from a single plasmonic metasurface and compare the structural forms of Au NPs observed in SEM images with their corresponding scattering colors and intensities (Fig. 3E). Each bit in the scattering PUF key from the plasmonic metasurface corresponds to a 670 × 670 nm surface area, containing an average of 54 Au NPs and matching 10 × 10 pixels in the scattering image obtained through a ×100 objective lens. As expected, the 8 bright local areas mostly contain high proportions of oligomeric Au NPs when \({R}_{{oligo}/{mono}} > 1\) (Fig. 3F, total 18 in Fig. S4). In contrast, the dark local areas are predominantly occupied by the monomeric Au NPs when R_oligo/mono < 1 or with the surface coverage below 24%. Isolating the red channel in these scattering regions enhances the color contrast as a function of R_oligo/mono, making it more distinct (Fig. 3G). This allows us to digitize the image into binary responses (0 and 1) by applying a threshold value of 128 to the red channel, whereas the green and blue channels do not produce functional results (Fig. S5). These observed trends align closely with the numerical simulations presented in Fig. 2F, establishing a robust foundation for generating a binary PUF response from the original scattering image (Fig. 1C for the PUF key generation process). For the overall analysis, we utilize a 50 × 50-bit array of the PUF key by binning 500 × 500 pixels from the scattering image, which corresponds to a 33.5 × 33.5 μm area of the quasi-ordered plasmonic metasurface, ensuring efficient image processing.

Performance of scattering PUF keys

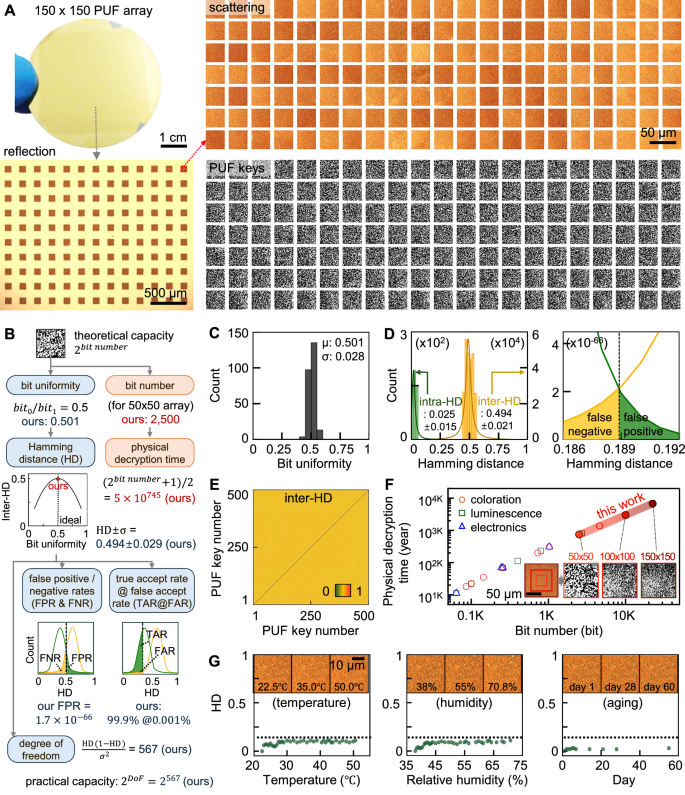
To systematically evaluate the performance of scattering PUF keys, we fabricate 22,500 PUF keys using Au NPs with a surface coverage of 25% on an array of square HfO₂ patterns (100 × 100 µm surface area, 25 nm thickness, Fig. 4A). The electrostatic coating process enables rapid, selective ‘pick-and-place’ assembly of Au NPs onto the HfO₂ regions, leaving the surrounding Au surfaces clean. To statistically evaluate the performance of an infinitely large set of PUF keys based on the small sample technique⁵⁰, we randomly select 500 quasi-ordered plasmonic metasurfaces, all of which exhibit nearly identical reflective hues to the human eye, with negligible perceptible variation (left panel of Fig. 4A). Meanwhile, each metasurface contains unique, unclonable stochastic scattering patterns (right panel of Fig. 4A), enabling the generation of individual PUF keys encoded as binary data (0 and 1) in 50 × 50-bit array (Fig. 4C). The recording and processing time is on the order of seconds, with the potential for further optimization via computational algorithms⁵¹. Crucially, the bit uniformity between the 0 and 1 responses across all 500 PUF keys closely approaches the ideal value of 0.5 (average: 0.501, standard deviation: 0.028, Fig. 4C). This uniformity is preserved across variations in light intensity, integration time, incident angle, and camera digital gain (Fig. S6), ensuring robustness in real-world scenarios. Although the scattering behavior in plasmonic metasurfaces is influenced by the mirror–nanoparticle coupling, which exhibits a resonance within the 45–90° range of incident light angles⁵², most ×100 objective lenses essential for high-resolution scattering imaging have a numerical aperture exceeding 0.7, inherently satisfying this angular requirement and eliminating any angular dependence. This consistency provides a robust foundation for reliable PUF performances (see Figs. 4B, S7, and Supplementary Note 1 for details).

Fig. 4: Performance of scattering PUF keys.

A Wafer-scale plasmonic metasurfaces (top), reflection (bottom). scattering images of fabricated plasmonic metasurfaces (each area: 100 × 100 μm), and their generated PUF keys (right). B A diagram illustrating the correlations between PUF performance metrics and C bit uniformity, D inter- and intra-Hamming distances (left), Gaussian fits (right), and E 2D pair inter-Hamming distances. F Average physical decryption times of the scattering PUF keys with different bit arrays (50 × 50, 100 × 100, and 150 × 150), compared with 36 literatures^{22,24,29,30,31,35,36,37,38,64,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96}. G Thermal, humid, and aging stabilities of the scattering PUF key.

We then firstly consider the Hamming distance, which quantifies the uniqueness of PUF keys and ideally approaches 0 when the same PUF key is measured multiple times (left panel of Fig. 4D)⁵³. This intra-Hamming distance reflects the stability of both the detecting device and method, and in our case, it is found to be 0.025 (standard deviation: 0.015), indicating high detection fidelity. In contrast, when calculating the inter-Hamming distances among all possible 500 PUF key pairs, we obtain an average of 0.494 (standard deviation: 0.021, Fig. 4E), confirming the high uniqueness of the scattering PUF keys. To establish a robust authentication threshold, we fit the intra- and inter-Hamming distance distributions to Gaussian profiles, identifying a crossover threshold of 0.189 (right panel of Fig. 4D). This threshold results in a false negative rate (\(3.8\times {10}^{-71}\)) and a false positive rate (\(1.7\times {10}^{-66}\)), comparable to or lower than those previously reported values (Table S2). The crossover profiles further define the true acceptance rate at false acceptance rate (TAR@FAR), a key metric for evaluating authentication security^32,54. For example, a system achieving TAR 90% @ FAR = 0.001% successfully blocks 99.999% of unauthorized access while allowing 90% of legitimate users to pass. Our scattering PUF system exceeds this standard, achieving TAR 99.9% @ FAR = 0.001% at a Hamming distance threshold of 0.40121, surpassing the TAR > 95% @ FAR = 0.01% benchmark set for biometric authentication systems such as fingerprint and iris recognition⁵⁵. Furthermore, binary bit streams extracted from the scattering PUF keys successfully pass all seven statistical tests, as officially approved by the National Institute of Standards and Technology (NIST SP 800-22, Table S3)⁵⁶, ensuring the randomness and reliability of the generated security keys. Then, the practical key capacity of a 50 × 50-bit PUF key is statistically estimated from the degree of freedom in inter-Hamming distance distributions. While the theoretical maximum for a 50 × 50-bit arrayed PUF key is 2²⁵⁰⁰, the practical key capacity of our system is estimated at \({2}^{567}\), sufficient to assign a unique PUF key to every item in the global population (~8 billion)⁵⁷. This scalability is attributed to the high degree of freedom in this PUF key system.

On the other hand, the physical decryption time required for physical decryption under random guessing attacks is primarily dependent on the bit number (Fig. S8)³⁰. Since fabrication details of PUF keys may be publicly available through research publications or patents, potential attackers could attempt to replicate PUF keys through iterative replacement until successful authentication is achieved. To estimate the physical decryption time under such conditions, we assume that attackers iteratively swap counterfeit PUFs until an identical key is found. Under this scenario, the estimated average physical decryption time is 5 × 10⁷⁴⁵ years for a scattering PUF key with a 50 × 50-bit arrays, increasing up to 10⁶⁷⁷³ years for a 150 × 150-bit arrays, longer than previous optical and electrical PUF keys (Fig. 4F). This renders the false authorization almost impossible within a human lifespan.

Beyond these security metrics, environmental stability is crucial for real-world implementation, as randomly structured nanomaterials often undergo restructuring, corrosion, or degradation under external stimuli (e.g., heat, moisture, mechanical stress, light source condition)^41,58. Such changes could alter the scattering properties of the PUF, compromising authentication integrity. To assess durability, we analyze the scattering PUF key under varying temperatures from 22.5 to 50.5 °C at 38% relative humidity (left panel of Figs. 4G, S9A), and under varying relative humidity from 38 to 70.8% at a constant temperature of 24 °C (middle panel of Figs. 4G, S9B). Note that the scattering images remain unchanged across all conditions, with the Hamming distance consistently below the 0.189 threshold, confirming the PUF key’s resilience. Furthermore, over a two-month observation period, only negligible changes are noted with a maximum Hamming distance of 0.03, still below the threshold, stemming from the use of chemically inert inorganic materials in the scattering PUF key (right panel of Fig. 4G, S10). These results confirm that our PUF keys maintain signal integrity despite external environmental changes, ensuring their feasibility for practical security applications in textiles, pharmaceuticals, and high-value consumer goods^30,59.

Colorful plasmonic metasurfaces with scattering PUF keys

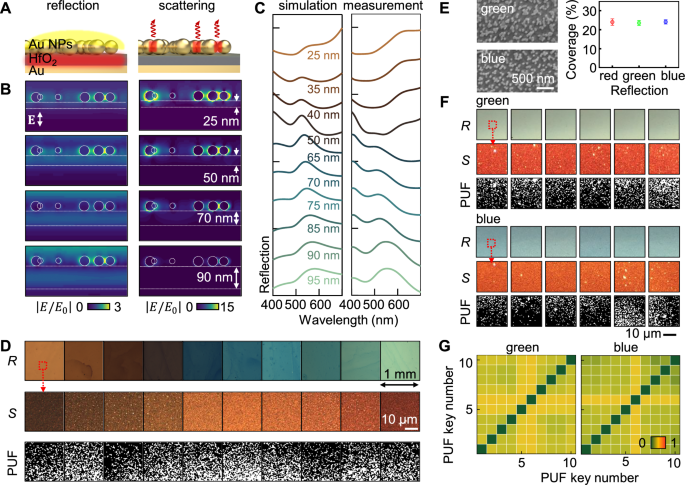
The beauty of Fabry-Perot etalon resonators lies in their ability to produce vivid reflective colors, which can be finely tuned across the visible spectrum by simply adjusting the thickness of the dielectric gap⁴¹. This straightforward yet powerful mechanism is also crucial in engineering the far-field reflective colors of the quasi-ordered plasmonic metasurface (Fig. 5A). As the gap thickness varies from 25 to 95 nm, the wavelength of light trapped within the gap between the Au NPs and the mirror redshifts (left panel of Fig. 5B), allowing the far-field reflective color to cover the entire visible spectrum (see “Methods” and Fig. S11 for simulation details), Fig. 5C. This trend shows a strong qualitative agreement between simulation and experiment. The average reflectance of the fabricated quasi-ordered plasmonic metasurface exceeds 55%, making it clearly observable to the naked eye (top panel of Fig. 5D).

Fig. 5: Plasmonic metasurfaces with various dielectric gap.

A Plasmonic metasurface with gap-driven uniform reflection (left) and plasmonic oligomer-driven stochastic scattering (right). B Optical near-field enhancements of the plasmonic metasurfaces with different HfO₂ dielectric gaps (left: enhancements within gaps for reflection, right: enhancements between nanoparticles for scattering). C Associated reflection spectra (left: simulation, right: measurement), D reflection (top) and scattering images (middle), and their generated PUF keys (bottom). E Surface coverages of the total Au NPs at the given area of 2 × 2 μm for quasi-ordered plasmonic metasurfaces exhibiting red, green, and blue reflective colors. F Associated reflective colors from various devices and their scattering and generated PUF keys with G 2D pair inter-Hamming distances (left: green, right: blue).

Conversely, despite variations in the gap thickness, the scattering from these color-varying plasmonic metasurfaces retains stochastic features with a reddish hue and an intensity of ~5%, along with high spatial resolution (middle panel of Fig. 5D). This is attributed to the optical near-field coupling of oligomeric Au NPs on the mirror (right panel of Figs. 5B, S12) and remains independent of the gap-driven reflective colors, enabling all plasmonic colors to generate unique scattering PUF keys (bottom panel of Fig. 5D), unattainable with existing plasmonic metasurfaces as demonstrated in Fig. 1B²⁷. We further verify the uniqueness of PUF keys for green and blue, fabricated at gap thicknesses of 90 nm and 65 nm, respectively, while maintaining a constant surface coverage of Au NPs (~24%) (Fig. 5E). This consistent surface coverage ensures the uniqueness of PUF keys while displaying uniform reflective colors (Fig. 5F), with mean inter- and intra-Hamming distances of 0.48 and 0.015, confirming weak correlation between different PUF keys (Figs. 5G, S13). Thus, regardless of the reflective color seen by the human eye, these quasi-ordered plasmonic metasurfaces inherently produce unclonable stochastic scattering patterns, making them ideal for colorful camouflage with hidden authentication codes.

Application of plasmonic camouflages with scattering PUF keys

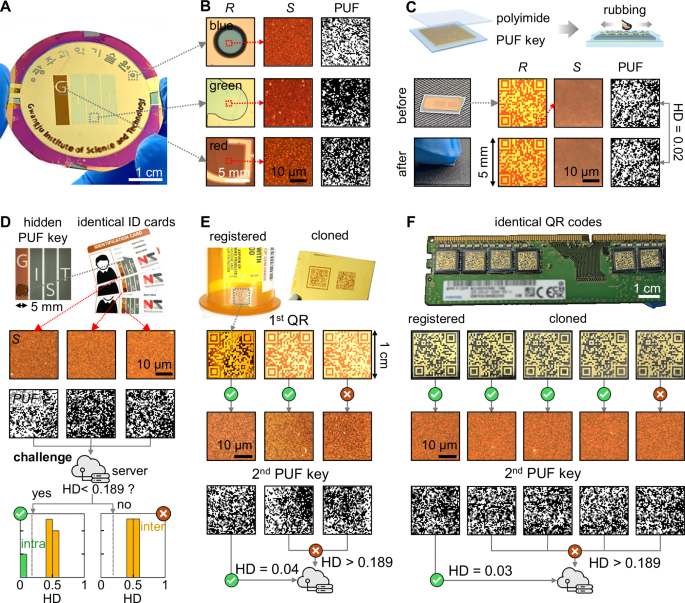
The quasi-ordered plasmonic metasurface uniquely integrates stochastic scattering PUF keys with tunable far-field reflective colors, enabling camouflage or selective highlighting of authentication information. This dual functionality makes it an ideal platform for covert security applications (Fig. 6). Utilizing the color palette obtained by varying the thickness of the dielectric gap, we fabricate a university logo with primary RGB colors, each corresponding to a specific thickness of the HfO₂ gap thickness (red: 35 nm, green: 90 nm, blue: 65 nm, Fig. 6A). A three-step shadow mask patterning process permits to deposit various sections of HfO₂ patterns with varying thicknesses on a 2-inch Au mirror (Fig. S3B), followed by uniform electrostatic self-assembly of Au NPs at 25% surface coverage (see Supplementary Video 1). Despite differences in dielectric thickness, each patterned region maintains high reflectance (>50%), making the colors clearly visible (left panel of Fig. 6B). More importantly, while these regions exhibit uniform far-field reflection, they simultaneously generate distinct stochastic near-field scattering, allowing each area to encode a unique PUF key (middle and right panels of Fig. 6B). To enhance mechanical durability for real-world applications, we encapsulate the metasurface with a transparent, scattering-free polyimide layer (50 μm thickness, Fig. 6C). This protective layer effectively protects against mechanical damage while maintaining authentication accuracy. Even after repeated abrasion tests (Supplementary Video 2), the metasurface retains its optical properties, with a Hamming distance of 0.02, confirming minimal alteration.

Fig. 6: Plasmonic camouflages with scattering PUF keys.

A Plasmonic RGB colorations with different HfO₂ thicknesses (red: 35 nm, green: 90 nm, blue: 65 nm), and B their RGB uniform reflection images (left), stochastic scattering images (middle), and generated PUF keys (right). C Scheme of the plasmonic metasurface fabricated on a flexible device and the attachment of a protective film (left), along with the verification of PUF robustness against physical stress (right). D Three different ID cards with hidden scattering PUF keys (left) and their use for authentication (right). E A lithographically patterned QR code-shaped metasurface on a flexible substrate and its cloned counterfeit QR code (top). The authentication process of a dual-layer authentication system using the QR code and hidden PUF key (bottom). F The QR codes on black semiconductor chips (top) and the authentication process using the camouflaged PUF keys within the QR codes (bottom).

Then, for secure identity verification, the quasi-ordered plasmonic metasurface is integrated into a red-brown section of the university logo on an authentic identification (ID) card, completely concealing the scattering PUF key by matching its reflective color (with 20 nm HfO₂ gap, CIE code: 61.1, 56.9) to the surrounding color (CIE code: 70.5, 61.4), Fig. 6D. This integration ensures that the PUF key remains invisible to the naked eye, preventing tampering or counterfeiting. To evaluate authentication performance, we pre-register the PUF key in a secure data server and fabricate two cloned ID cards from the same batch of metasurfaces. The authentication process involves (Fig. S14), (1) capturing the scattering pattern using a dark-field optical microscope, (2) extracting the unique PUF key using a custom Python algorithm (middle panel of Fig. 6D), and (3) comparing the extracted key with the database, using Hamming distance thresholding at 0.189 (right panel of Fig. 6D). The authentic ID card produces a Hamming distance below 0.189, confirming its legitimacy, while both cloned ID cards exceed this threshold and fail authentication. This verification process takes only 2.2 s, with potential for further acceleration through optimization of the sorting algorithm⁶⁰. Thanks to the low false positive/negative rates of quasi-ordered plasmonic metasurfaces, cloning is nearly impossible, significantly enhancing security for identity verification systems.

Beyond concealment, this selective visual integration also enables targeted exposure, offering a promising anti-counterfeiting solution for various products. Building on this concept, we extend our approach to enhance QR code security by embedding hidden PUF keys within matching color regions (Fig. 6E). Quick-response (QR) codes are widely used for product tracking, payments, and authentication, yet remain vulnerable to unauthorized duplication⁶¹. To mitigate this risk, we fabricate quasi-ordered plasmonic metasurfaces on a flexible polyimide film, integrating them directly into QR code regions patterned through photolithography. Since QR codes must remain clearly visible regardless of background color while simultaneously concealing embedded PUF keys, selective visualization of the reflective color against the background is crucial. To demonstrate this, we apply orange- and light green-reflective metasurfaces to two different surfaces: a transparent plastic case and the black semiconductor chips of a random access memory (RAM) module (top panels of Fig. 6E, F). In particular, on the black chip, the green-reflective metasurface contrasts sharply against the dark background, making the PUF key visually distinguishable for authentication. While the QR code itself enables rapid identification (middle panels of Fig. 6E, F), counterfeit risks persist if multiple items share the same QR code. To prevent this, the embedded hidden PUF key is cross-verified with the server’s record, ensuring authenticity (bottom panels of Fig. 6E, F). This dual-layer security approach guarantees that even if a QR code is cloned, the underlying PUF key remains unclonable, providing an additional safeguard against counterfeit goods.

The flexible nature of the polyimide-based metasurfaces potentially allows for attachment to a wide range of products, making them ideal for securing pharmaceuticals (e.g., drug packaging with invisible authentication layers to prevent medication fraud)³⁵, luxury goods (e.g., handbags, watches, and jewelry with hidden PUFs for counterfeit protection), high-value electronics, and cosmetics with tamper-proof security labels⁶². Considering economic feasibility, while the use of gold increases unit costs (Table S1), it remains adaptable for mass production, particularly in luxury and high-value markets. Although high-magnification microscopes are used here, portable dark-field microscopes integrated with smartphone cameras are emerging as low-cost, user-friendly authentication tools⁶³. These advancements suggest that real-time, consumer-accessible authentication systems could soon be implemented without requiring laboratory-grade microscopes. Overall, the scalability, flexibility, and industrial feasibility of these metasurfaces position them as a next-generation security solution for covert authentication and anti-counterfeiting applications.

We successfully demonstrate quasi-ordered plasmonic metasurfaces, exhibiting tunable structural coloration without compromising either far-field uniformity or near-field stochasticity—an ability rarely observed in artificial systems. Through the electrostatic self-assembly of gold nanoparticles on a patterned metallic mirror, we achieve precise control over reflective colors across the visible spectrum by engineering the dielectric gap thickness, while simultaneously generating stochastic scattering patterns that function as robust physically unclonable functions. This approach unlocks a new paradigm in security authentication, where optical visualization and covert identification coexist. These PUF keys, rigorously validated through NIST SP 800-22 statistical testing, exhibit exceptional uniformity, uniqueness, and stability across all colors, ensuring unprecedented reliability against duplication. Notably, the PUF performance can be further enhanced through increased imaging resolution or expanded fabrication areas, both enabling extended bit number (thus increasing physical decryption time). Moreover, we demonstrate real-world applications by integrating these metasurfaces into concealed security elements, such as camouflaged PUF keys in ID cards and embedded authentication in QR codes, showcasing their viability for next-generation anti-counterfeiting technologies^30,64. The scalable manufacturing process and intrinsic authentication capability further offer promising integration with plasmonic sensing⁶⁵, imaging⁶⁶, and display technologies⁶⁷, paving the way for cost-effective, industrial-scale adoption while maintaining high security and uniqueness.

Numerical simulation

Optical properties of plasmonic metasurfaces are calculated using a commercial FDTD simulation program (Ansys Lumerical). 50 nm Au NPs are randomly distributed with 24% surface coverage (30 particles in 0.25 μm² square) on a Au film, spaced with a dielectric HfO₂ gap. In order to match experimental conditions, a white light (ranging from 400 nm to 700 nm) is illuminated onto the film with a normal incidence for reflectance. Meanwhile, for scattering, a linearly polarized scattered-field source propagates along the film surface. The optical properties of Au and HfO₂ are extracted from the literature^68,69.

Synthesis of colloidal Au NPs

The colloidal solution of Au NPs is synthesized using the Turkevich method⁷⁰. 100 mL of 0.25 mM sodium tetrachloroaurate (III) dihydrate (NaAuCl₄, Sigma-Aldrich) is stirred at a temperature of 95 °C for 20 min, and 0.45 mL of 0.485 mM trisodium citrate (Na₃C₆H₅O₇, Sigma-Aldrich) is added to this solution. After 20 min, the solution color turns red, indicating the synthesis of 50 nm Au NPs.

Growth of thin films

A 150 nm thick Au film is deposited on a 2-inch silicon wafer using an electron evaporation method at a growth rate of 0.1 nm/s. For a flexible PUF, a 50 nm thick Au film is deposited on a polyimide film (Sungho Sigma). During deposition, the substrate is cooled to −35 °C and azimuthally rotated with 300 rpm of the rotation speed. Subsequently, an HfO₂ film is deposited with various thicknesses, ranging from 25 nm to 95 nm, onto the Au film using the same method at a growth rate of 0.05 nm/s with the substrate cooling. For patterning HfO₂ film and QR codes (e.g., Figs. 3C, 6E), a photoresist (AZ-5214, Sigma-Aldrich) is spin-coated onto the Au substrate at 4000 rpm for 35 s and soft-baked at 110 °C for 90 s. The photoresist is then exposed under 20 mW/cm² UV light (400 nm wavelength) using a mask aligner (M100, Prowin) for 7 s and developed in 300 MIF (Sigma-Aldrich) for 30 s.

Electrostatic nanoparticle coating

The Au NPs dispersed in solution are electrostatically transferred onto the HfO₂/Au films and patterns⁴⁵. The concentration of colloidal Au NPs is adjusted to 0.1 vol.% and dispersed in the mixture of 2.5 mM HCl and 0.25 mM trisodium citrate. This colloidal solution is then drop-cast onto the HfO₂/Au film, enabling the electrostatic attraction between the negatively charged Au NPs and the positively charged HfO₂ film. The change in the coating time from 1 to 60 s effectively tunes the surface coverage of the nanoparticles, ranging from 8 to max. 24%. Furthermore, the nature of the electrostatic force enables selective Au NPs coating only on the reversely charged HfO₂ pattern while remaining clean on the bare Au surface (due to the repulsion).

SEM analysis

The structures of plasmonic metasurfaces are imaged using SEM (SU5000, Hitachi) under an accelerating voltage of 15 kV. Three positions with 2.13 × 1.4 µm area for each sample are randomly selected to analyze the surface coverages of the Au NPs within them. The forms of monomer and oligomer are separated by thresholding the effective surface area of 750 nm² (i.e., theoretical area of 50 nm monomer). Also, the cross-sectional views of SEM images are used to measure the thickness of the plasmonic metasurfaces.

Optical imaging and spectroscopy

Bright- and dark-field optical images and spectra of the plasmonic metasurface are obtained using a CCD camera (STC-MCS500U3V, Sentech) and spectrometer (Ocean Optics QEpro) through ×5 objective (Olympus LMPLFLN-BD, numerical aperture 0.15) and ×100 objective (Olympus MPLFLN-BD, numerical aperture 0.9, Olympus LMPLFLN-BD, numerical aperture 0.8) in a customized microscope (Olympus BX51). The white light source is a halogen lamp (PHILIPS 7724, 4.33 mW).

Generation of scattering PUF keys

Scattering images of the plasmonic metasurfaces are split into 3 RGB color channels. Each R channel is selectively used to generate PUF keys such that they are cropped into 500 × 500 pixels and binned to an image size of 50 × 50 pixels. To digitize the data, threshold is applied at the level of 128 and interpreted to binary bit stream by decoding dark pixel (<128) as a response ‘0’ and bright pixel (>128) as a response ‘1’.

References

Authors and Affiliations

1. Department of Electrical Engineering and Computer Science, Gwangju Institute of Science and Technology, Gwangju, Republic of Korea

   Gyurin Kim, Doeun Kim, JuHyeong Lee, Juhwan Kim, Se-Yeon Heo, Young Min Song & Hyeon-Ho Jeong

2. Department of Semiconductor Engineering, Gwangju Institute of Science and Technology, Gwangju, Republic of Korea

   Young Min Song & Hyeon-Ho Jeong

3. Artificial Intelligence (AI) Graduate School, Gwangju Institute of Science and Technology, Gwangju, Republic of Korea

   Young Min Song

4. School of Electrical Engineering, Korea Advanced Institute of Science and Technology, Daejeon, Republic of Korea

   Young Min Song

Contributions

G.K., Y.M.S. and H.-H.J. designed experiments. G.K., J.L. performed the simulation. G.K. and D.K. performed the sample fabrication. G.K. performed optical measurement and SEM analysis with support from J.K. S.-Y.H. and G.K. performed Python coding for PUF generation and analysis. G.K., Y.M.S. and H.-H.J. wrote the paper, and all authors contributed to editing.

Corresponding authors

Correspondence to Young Min Song or Hyeon-Ho Jeong.

Competing interests

The authors filed one patent application related to the principle and fabrication method. There are no other competing interests.

Peer review information

Nature Communications thanks Thomas Just Sørensen and Diederik Wiersma for their contribution to the peer review of this work. A peer review file is available.

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions