Preparation of a neutral nitrogen allotrope hexanitrogen C2h-N6 – Nature

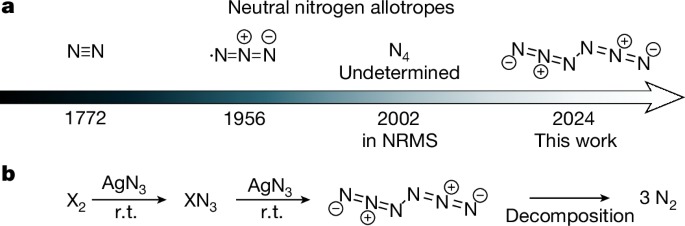
Molecular nitrogen allotropes beyond N₂ are promising for the development of high-energy-density materials⁴ because they release enormous energy on dissociation into gaseous N₂. As the main component of air, N₂ is inert, non-toxic and not a greenhouse contributor^5,6,7. Unlike carbon, N₂ is the only nitrogen allotrope found in nature and strategies for synthesizing higher neutral molecular nitrogen allotropes are highly sought after^{8,9,10,11,12,13,14}. However, they are deemed extremely unstable, especially when uncharged and with an even electron count¹⁵. Consequently, only two examples have been reported. The azide radical (•N₃) (Fig. 1a) was identified in the gas phase through rotational spectroscopy in 1956 (refs. ^16,17). In 2002, N₄ was detected by gas-phase neutralization-reionization mass spectrometry (NRMS); its structure has not been revealed¹⁸. The intermediacy of an N₆ species was tentatively suggested in 1970 in the decay of azide radicals in aqueous solution but no definitive spectroscopic evidence was provided¹⁹.

Fig. 1: All known neutral molecular nitrogen allotropes and preparation of N₆.

a, Discovery timeline (year given), composition and structure (the structure of N₄ has not been determined). b, Reaction sequence used in this study. r.t., room temperature.

There are many computations proposing molecular allotropes spanning from N₄ to N₁₂₀, including chains, rings and cages^7,20, most of which have low dissociation barriers into N₂. For example, hexazine (cyc-N₆, the nitrogen analogue of benzene) exhibits a computed barrier of only 4.2 kcal mol⁻¹ for decomposition into three N₂ (ref. ²¹). Quantum mechanical tunnelling (QMT) effects could further reduce the lifetime of higher nitrogen allotropes, adding to their difficulty of preparation²².

Although the pursuit of higher neutral molecular nitrogen allotropes is extremely challenging, several homonuclear polynitrogen ions have been isolated. The synthesis and characterization of [N₅]⁺[PnF₆]⁻ (Pn = As, Sb) salts with a bent pentanitrogen cation represents a milestone^23,24. Christe et al. initially identified the \(cyclo{{\rm{-N}}}_{5}^{-}\) anion using mass spectrometry in 2002 and 2003 (refs. ^25,26) and Zheng et al. reported in 2017 the synthesis of a salt featuring the \(cyclo{{\rm{-N}}}_{5}^{-}\) anion²⁷. The synthesis of various metal pentazolates was achieved through the reaction of [Na(H₂O)(N₅)]•2H₂O with metal salts^28,29.

In the realm of solid-state (non-molecular) structures, a breakthrough was the high-temperature (2,000 K), high-pressure (110 GPa) diamond-like solid-state cubic gauche nitrogen phase in which all atoms are connected by single bonds^30,31. An aromatic cyclic hexazine \({{\rm{N}}}_{6}^{4-}\) was identified through solid-state X-ray diffraction of K₉N₅₆ under pressures above 40 GPa and temperatures above 2,000 K (ref. ³²). Greschner et al. predicted a new nitrogen molecular crystal comprising N₆ units with an open-chain structure stabilized by electrostatic interactions³³, in line with assessments for the molecular species⁹.

In our analysis of the proposed molecular nitrogen allotropes, acyclic neutral N₆ (hexaaza-1,2,4,5-tetraene, hexanitrogen, diazide) stands out because N₂ moieties are not discernible (Fig. 1). The central N–N bond would lead to unproductive endothermic dissociation (ΔG_298K theor. +26.1 kcal mol⁻¹, vide infra) into two •N₃. Furthermore, the computed dissociation barrier into three N₂ molecules of ΔG^‡_298K = 14.8 kcal mol⁻¹ makes N₆ a promising candidate for synthesis. Here we show that N₆ indeed can be prepared at room temperature through the reaction of Cl₂ or Br₂ with AgN₃ under reduced pressure, followed by cryogenic trapping³⁴. The characterization was accomplished by infrared (including ¹⁵N-isotope labelling) as well as UV-Vis spectroscopy and ab initio computations. We also demonstrate the preparation and stability of C_2h-symmetric N₆ (hereinafter referred to as N₆) in neat form as a film at the temperature of liquid nitrogen (77 K).

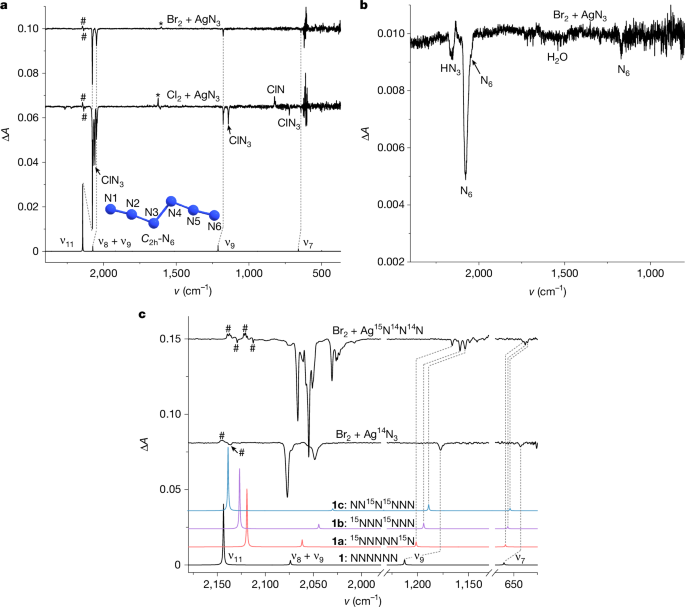
As AgN₃ is an excellent reagent for the synthesis of polyazides³⁵ and halogen azides both in the gas phase³⁶ and in solution^37,38, we suggest that the reaction of AgN₃ with XN₃ (X = halogen) is a viable route to N₆ (Fig. 1b). The reactions were conducted in either a quartz tube or a U-trap by flowing gaseous Cl₂ through solid AgN₃ under reduced pressure at room temperature (see the ‘Synthesis details’ section in Methods and Supplementary Fig. 1). Apart from the known bands of ClN₃ (ref. ³⁹) and HN₃ (ref. ⁴⁰), a distinct group of bands at 2,076.6, 2,049.0, 1,177.6 and 642.1 cm⁻¹ was recorded (Supplementary Fig. 2). After irradiating the matrices with 436 nm light (Fig. 2a middle trace and Supplementary Fig. 3), all bands vanish. However, the rates of decomposition of the newly observed infrared bands differ from those attributed to ClN₃ (Supplementary Figs. 4 and 5). There were no discernible products other than chloronitrene (ClN) detected in the difference spectrum after irradiation. Furthermore, identical bands were detected when Br₂ was used instead of Cl₂, indicating that the unidentified species does not contain halogens (Fig. 2a upper trace and Supplementary Fig. 6). Also, BrN₃ does not decompose on 436 nm irradiation, providing clean decomposition spectra of the yet unidentified species.

Fig. 2: Infrared spectra of N₆ isotopomers and side products.

a, Lower trace: computed anharmonic infrared spectrum of N₆ at B3LYP/def2-TZVP, including the ν₈ + ν₉ combination. Middle trace: difference spectrum showing the changes after 8 min of 436 nm irradiation of the products of the reaction of Cl₂ with AgN₃. Upper trace: difference spectrum showing the changes after 6 min of 436 nm irradiation of the reaction products of Br₂ with AgN₃. b, Difference spectrum of a neat N₆ film at 77 K showing the changes after 8 min of 436 nm irradiation. c, Bottom to top traces: computed anharmonic infrared spectrum of N₆, ¹⁵NNNNN¹⁵N (1a), ¹⁵NNN¹⁵NNN (1b) and NN¹⁵N¹⁵NNN (1c) at B3LYP/def2-TZVP, including the ν₈ + ν₉ combination; difference spectrum showing the changes after 8 min of 436 nm irradiation of the reaction products of Br₂ with AgN₃; difference spectrum showing changes after 8 min of 436 nm irradiation of the reaction products of Br₂ with Ag¹⁵N¹⁴N¹⁴N. Matrix sites from natural abundance and isotope-labelled HN₃ (#) and H₂O (*) are marked.

The intensive vibrational band at 2,076.6 cm⁻¹ compares favourably with the asymmetric stretching band of the azide moiety in isoelectronic N₃–NCO (2,099.1 cm⁻¹, Ar matrix)⁴¹. Compared with the computed harmonic vibrations at CCSD(T)/cc-pVTZ, the four bands noted above could be attributed to N₆, except the band at 2,049.0 cm⁻¹ of moderate intensity, although it disappeared together with the other bands following photolysis (Supplementary Figs. 4 and 7). To determine the origin of the band at 2,049.0 cm⁻¹, anharmonic vibrational frequencies were computed at B3LYP/def2-TZVP (Supplementary Table 1). This analysis indicates that this band derives from a combination of fundamentals ν₈ (a_g symmetric N³N⁴ stretching mode) and ν₉ (b_u asymmetric N³N²N¹ stretching mode). The substantial anharmonic intensity contribution (219 km mol⁻¹; Supplementary Table 2) of the fundamental ν₁₁ at 2,143.5 cm⁻¹ and the ν₈ + ν₉ combination is notably stronger than its fundamentals, suggesting that the combination ν₈ + ν₉ gains energy through Fermi resonance from the adjacent strong fundamental ν₁₁ (ref. ⁴¹).

To confirm our assignments, isotope-labelling experiments were conducted using Ag¹⁵N¹⁴N¹⁴N. Three groups of distinct peaks can be discerned in the infrared spectra (Fig. 2c and Supplementary Fig. 8), indicating the presence of two N₃ moieties in the molecule, which can be attributed to three types of isotopomer (1a: ¹⁵NNNNN¹⁵N, 1b: ¹⁵NNN¹⁵NNN, 1c: NN¹⁵N¹⁵NNN), respectively. In particular, the unsymmetric isotopic substitutions in 1b lower its point group from C_2h to C_s. Computations delineate that the terminal (N¹ or N⁶) and internal (N³ or N⁴) ¹⁵N substitutions mainly influence the terminal (ν₁₁) and internal asymmetric stretching vibration (ν₉) of the N₃ moieties, respectively. This leads to a redshift of the ν₈ + ν₉ combination and a blueshift of the ν₁₁ fundamental in going from 1a to 1c, resulting in their gradual separation. The intensity ratio of the ν₈ + ν₉ combination and the ν₁₁ fundamental in 1a is nearly 1:1, which is much higher than that in 1c (about 1:17). These findings align well with the anharmonic infrared intensities computed by density functional theory (Supplementary Table 3), which are attributed to the closer proximity of the ν₈ + ν₉ combination to the strong ν₁₁ fundamental in 1a, resulting in an increase of the Fermi resonance and vice versa in 1c. Statistically, the anticipated ratio of the three isotopomers should be 1a:1b:1c = 1:2:1, which is reflected in the observed fundamental ν₇ in the experimental spectrum (Fig. 3). Furthermore, the computed intensity of ν₉ in 1c (107 km mol⁻¹; Supplementary Table 3) is higher than that in 1a (92 km mol⁻¹) and 1b (98 km mol⁻¹), which matches the intensity ratios of ν₉ observed in 1a and 1b (approximately 1:2). The experimentally observed intensities agree with these findings and show a slightly higher intensity of ν₉ in 1c than in 1a.

Fig. 3: Measured and computed UV-Vis spectrum of N₆ and molecular orbitals involved in the electronic transitions.

Experimental difference UV-Vis spectrum reflecting changes following 4 min of 436 nm irradiation of the reaction products of Br₂ with AgN₃ in argon at 10 K. Inset, computed [TD-B3LYP/def2-TZVP] electronic transitions for N₆ and molecular orbitals involved.

To explore the intrinsic stability of N₆, we also prepared neat N₆ at room temperature and condensed it at liquid nitrogen temperature (77 K) as a film on the surface of the matrix window without using argon as a host gas. Irradiation of such N₆ films resulted in very similar spectral changes as those observed in argon matrices at 10 K (Fig. 2b and Supplementary Fig. 9). That is, neat N₆ is sufficiently stable at the temperature of liquid nitrogen to allow its direct identification.

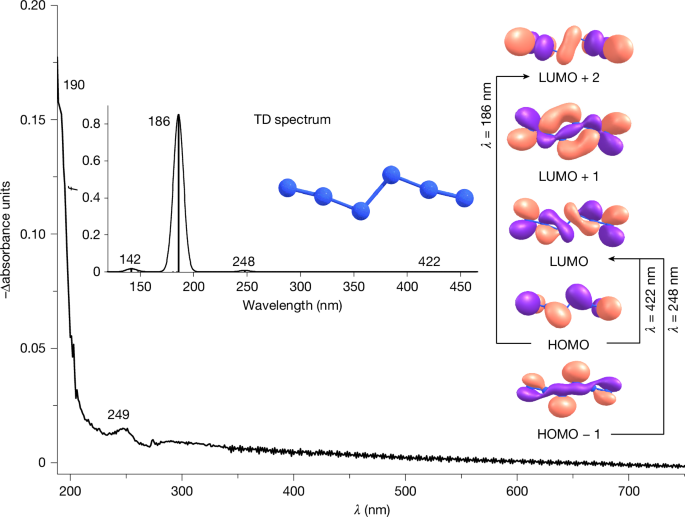
Further evidence is provided by the UV-Vis spectrum of N₆. After 6 min of 436 nm irradiation of the reaction products of Br₂ with AgN₃, we observed the disappearance of the transitions at 190 and 249 nm and, consistent with the infrared experiments, no new transitions appeared (Fig. 3). All transitions correlate well with the values for the electronic excitations of N₆ at 186 nm (f = 0.8512) and 248 nm (f = 0.0078) computed at [TD-B3LYP/def2-TZVP]. Furthermore, the computations reveal a weak electronic excitation at 422 nm (f = 0.0004), corresponding to a π → π* transition, which aligns well with the observed photochemistry.

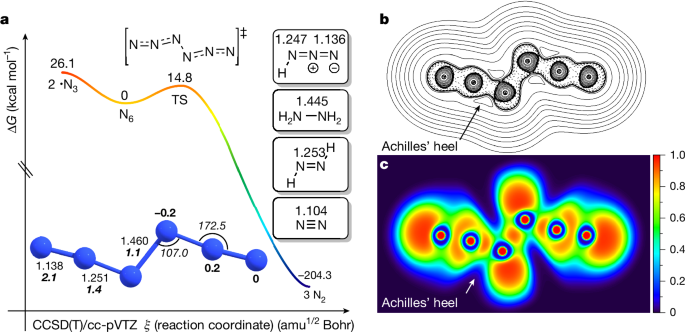
To better understand the structure and the potential energy landscape of N₆, we computed its energy profile at CCSD(T)/cc-pVTZ (Fig. 4a (ΔG_298K) and Supplementary Fig. 10 (ΔH₀); see the ‘Computational details’ section in Methods). Only the C_2h-N₆ trans-conformer is a local minimum; the C_2v-N₆ cis-conformer is a higher-order stationary point and chemically not relevant^42,43. The formal double bond lengths in the N₃ moieties are much longer than the triple bond in N₂ (theor. 1.104 Å; expt. 1.098 Å)⁴⁴, indicating double-bond character. Indeed, the computed N² = N³/N⁴ = N⁵ bond length (1.251 Å) is close to that of trans-diazene (HN = NH, theor. 1.253 Å; expt. 1.252 Å)⁴⁵. The structure of N₆ is different from the azide radical (•N = N = N, theor. 1.183 Å; expt. 1.181 Å)⁴⁶ but comparable with the N₃ moiety in hydrazoic acid (HN₃, theor. 1.247 and 1.136 Å; expt. 1.237 and 1.133 Å for the N¹ = N² and N² = N³ bonds, respectively). The N³–N⁴ bond in N₆ (1.460 Å) compares favourably with that in hydrazine (H₂N–NH₂, theor. 1.445 Å; expt. 1.446 Å). This geometric analysis is well captured by the Lewis structure of N₆ (Fig. 1). These conclusions are supported by natural bond orbital computations, which indicate that the terminal nitrogen atoms are electronically neutral, whereas small positive and negative charges are located at N² and N⁵ (+0.2e) as well as on N³ and N⁴ (−0.2e), respectively (Fig. 4a). Equally, N¹–N²/N⁵-N⁶ have the highest bond order (2.1), followed by N²–N³/N⁴–N⁵ (1.4) and N³–N⁴ (1.1).

Fig. 4: Computational analyses for N₆.

a, Potential energy profile (ΔG_298K, kcal mol⁻¹) for N₆ at CCSD(T)/cc-pVTZ. The optimized parameters of N₆ are given in Ångstrom (normal font), degrees (italics), natural charges in bold and natural bond orders in bold italics. Insets, computed NN bond lengths for N₂, trans-HNNH, hydrazine and HN₃ at CCSD(T)/cc-pVTZ. b, Contour line map of the Laplacian of the electron density of N₆; solid and dashed lines represent positive and negative regions, respectively. c, ELF map.

We visualized the Laplacian of the electron density to gauge where the bonds in N₆ are likely to break (Fig. 4b) and why the computed barrier for decomposition into three moles of N₂ is, compared with other systems, rather high (ΔG^‡_298K = 14.8 kcal mol⁻¹). This barrier implies appreciable kinetic stability that is mirrored by our observations. For comparison, the computed barrier of hypothetical D_2h-N₄ dissociating into two N₂ is 6.5 kcal mol⁻¹ at MR-AQCC/VTZ⁴⁷. With the electron density analysis, the ‘Achilles’ heel’ was discerned at the N²–N³/N⁴–N⁵ bonds, as evident from the vertex of positive Laplacian of the in-plane electron density. This is confirmed by the electron localization function (ELF) analysis⁴⁸ (Fig. 4c). Both the Laplacian of the electron density and the ELF analysis indicate the electron density minimum around the N²–N³/N⁴–N⁵ bonds. Hence, even though the Lewis structure would indicate N₆ breaking into two •N₃ radicals, that is, breaking of the central N³–N⁴ single bond, the computed barrier for this process amounts to sizeable ΔG_298K = 26.1 kcal mol⁻¹ and is unproductive.

On the other hand, ΔG^‡_298K for the elementary decomposition into three N₂ is 14.8 kcal mol⁻¹, implying a finite lifetime of N₆ at room temperature. As N₆ decomposition may be accelerated by QMT^21,22,49, we used canonical variational theory and small-curvature tunnelling computations at B3LYP/def2-TZVP that reveal that N₆, unlike hexazine (cyc-N₆)²¹, is unlikely to decompose through QMT, with an estimated half-life of N₆ of more than 132 years at 77 K (Supplementary Table 4). At 298 K, the computed half-life still amounts to 35.7 ms. This supports our finding that N₆ exists long enough in the gas phase at ambient temperature to be trapped subsequently in cryogenic matrices.

According to CCSD(T)/cc-pVTZ (ΔH₀) computations, the decomposition of N₆ into three N₂ is exothermic (ΔH₀) by 185.2 kcal mol⁻¹, which is 2.2 and 1.9 times higher than the decomposition enthalpies of TNT (2,4,6-trinitrotoluene) and HMX (1,3,5,7-tetranitro-1,3,5,7-tetrazocane, octogen) by weight⁵⁰ (see the ‘Computational details’ section in Methods).

We report here the facile synthesis and spectroscopic identification of experimentally unreported hexanitrogen N₆. This represents the first, to our knowledge, experimentally realized neutral molecular nitrogen allotrope beyond N₂ that exhibits unexpected stability. This discovery challenges the long-held belief of the elusiveness of neutral molecular nitrogen allotropes.

Matrix apparatus design

For the matrix isolation studies, we used an APD Cryogenics HC-2 cryostat with a closed-cycle refrigerator system, equipped with an inner CsI window for infrared measurements. Spectra were recorded at the temperature of the matrix (10 K) with a Bruker VERTEX 70 FT-IR spectrometer with a spectral range of 4,000–400 cm⁻¹ and a resolution of 0.7 cm⁻¹ and UV-Vis spectra were recorded with a Jasco V-670 spectrophotometer equipped with an inner sapphire window. A high-pressure mercury lamp (HBO 200, Osram) with a monochromator (Bausch & Lomb) was used for irradiation. Cl₂ or Br₂ was evaporated (Cl₂-CCl₄: −140 °C, Br₂: −85 °C) from a storage bulb into the quartz tube or U-trap. Although not directly measured, all reaction products were co-condensed with a large excess of argon (typically 60–120 mbar from a 2,000-ml storage bulb) onto the surface of the matrix window at 10 K in several milliseconds.

Synthesis details

Warning! Silver azide and halogen azides are extremely hazardous and explosive. Such compounds should be handled with utmost care and only in very small quantities (<5 mmol). Appropriate safety precautions (blast screens, face shields, Kevlar gloves, soundproof earmuffs and protective leather clothing) are necessary. Make sure to eliminate static electricity before handling. It is also crucial to avoid friction and light exposure and prevent any contact with metals during sample handling to ensure safety.

Silver azide was synthesized by adding a stoichiometric amount of a silver nitrate–water solution to a sodium azide–water solution in the dark. The precipitate was washed three times with anhydrous ethanol. The resulting slurry was loosely dispersed on one side of the inner surface of a straight quartz tube (ø 10 × 1) or the inner surface of a U-trap (inside diameter 10 mm) and then brought to reduced pressure to remove the solvent. Typically, 0.6 mmol and 2.5 mmol of AgN₃ are required for the straight quartz tube and U-trap, respectively. Na¹⁵N¹⁴N¹⁴N (>99% ¹⁵N, Sigma-Aldridge) was used for isotope labelling experiments. Chlorine gas was bubbled into CCl₄ at 0 °C and degassed before use. Bromine was purified by vacuum distillation before use. Typically, 3 mmol of halogen were stored in the storage bulb for the reaction.

Computational details

Geometry optimizations and energy computations were carried out at the CCSD(T)/cc-pVTZ^51,52,53 levels of theory using ORCA 5.0 (with keywords verytightscf and verytightopt)⁵⁴. B3LYP^55,56 computations (geometry optimizations, energy computations (all free energies were computed at 298 K), harmonic vibrational analysis and DVPT2 anharmonic vibrational analysis) were performed using Gaussian 16 (ref. ⁵⁷) with a def2-TZVP basis set⁵⁸. Local minima were confirmed by vibrational frequencies analyses and transition states were further confirmed by intrinsic reaction coordinate computations. Harmonic vibrational analysis at CCSD(T)/cc-pVTZ was performed using CFOUR v2.1 (ref. ⁵⁹). Wavefunction analysis (Laplacian of electron density and electron localization function) results were obtained from Multiwfn 3.8 (ref. ⁶⁰) at CCSD(T)/cc-pVTZ. Natural bond order analysis and resonance structures were computed with NBO 7.0 (refs. ^61,62). CVT/SCT (canonical variational transition state theory with small-curvature tunnelling) and CVT/ZCT (canonical variational transition state theory with zero-curvature tunnelling) computations were carried out with Gaussrate 17 (refs. ^{27,63,64,65,66,67}) as an interface between Gaussian 16 and Polyrate⁶⁸. Furthermore, local stretching force constants were obtained by LModeA-nano⁶⁹ as a plugin of the open-source version of the visualization program PyMOL.

Detonation calculation details

First, the density (ρ, in cm³ per molecule) of the N₆ crystal was determined using electrostatic interaction correction as suggested by Politzer et al.⁷⁰ (equation (2)). M_m (84.04/(6.02 × 10²³) g per molecule) is the molecular mass. V_m (610.52/(1.89 × 10⁸)³ cm³ per molecule) is the volume of the isolated gas-phase molecule, which was determined by the 0.001 a.u. density envelope using the marching tetrahedron method^60,71. ν is the parameter of balance between positive and negative surface potentials⁷² (equation (2)). \({\sigma }_{{\rm{tot}}}^{2}\) (48.40 kcal² mol⁻²) is the strengths and variabilities of the overall surface potentials, which could be derived from variance of positive (\({\sigma }_{+}^{2}\), 31.06 kcal² mol⁻²) and negative charges (\({\sigma }_{-}^{2}\), 17.34 kcal² mol⁻²) with equation (3). α (0.9183), β (0.0028) and γ (0.0443) are coefficients.

The detonation velocity (D) and detonation pressure (P) were calculated using the Kamlet–Jacobs equation⁷³ (equations (4) and (5)). N is the number of moles of the gas generated per gram (equation (6)), \(\bar{M}\) is the average molecular weight of the gaseous product (equation (7)), Q is the heat of detonation (equation (8)), M is the molecular weight (84.04 g mol⁻¹), ΔH_f is the standard heat of formation (774.88 kJ mol⁻¹, which was derived from the energy difference of the computed enthalpy at 298 K between C_2h-N₆ and 3 moles of N₂) and a (0), b (0), c (0) and d (6) represent the number of C, H, O, and N atoms in the molecule, respectively.

Assessing the energetic performance using the Kamlet–Jacobs equation⁷³, the CCSD(T)/cc-pVTZ level of theory predicts a lower density (ρ: 1.51 g cm⁻³) than that of TNT (1.65 g cm⁻³) and an excellent detonation performance (detonation velocity D: 8,930 m s⁻¹; detonation pressure P: 31.7 GPa). This compares favourably with several well-known explosives, for example, TNT (D: 6,900 m s⁻¹; P: 21.0 GPa), RDX (1,3,5-trinitro-1,3,5-triazinane; D: 8,750 m s⁻¹; P: 34.5 GPa) and FOX-7 (1,1-diamino-2,2-dinitroethylene; D: 8,870 m s⁻¹; P: 34.5 GPa)⁷⁴.

Energy-releasing equivalent calculation details

A kiloton of N₆ is 1.19 × 10⁷ mol, which can release an energy of 2.20 × 10⁹ kcal (9.21 terajoules) based on the enthalpy (ΔH₀). Considering that the standard kiloton TNT equivalent is 4.184 terajoules, N₆ can release 2.2 times the energy of TNT of the same weight. On the basis of the documented TNT equivalent based on weight for HMX (1.15) and RDX (1.15)⁵⁰, N₆ can release 1.9 times the energy of HMX or RDX with the same weight.

References

Authors and Affiliations

1. Institute of Organic Chemistry, Justus Liebig University Giessen, Giessen, Germany

   Weiyu Qian  (钱伟煜), Artur Mardyukov & Peter R. Schreiner

Contributions

W.Q., A.M. and P.R.S. conceived the project. W.Q. and A.M. designed and conducted the experiments, performed computations and collected all data. W.Q. wrote the original manuscript. W.Q., A.M. and P.R.S. revised the manuscript. A.M. and P.R.S. supervised the project.

Corresponding authors

Correspondence to Artur Mardyukov or Peter R. Schreiner.

Competing interests

W.Q., A.M., and P.R.S. are inventors on European patent application EP24194869 (16 August 2024), submitted by the Justus Liebig University Giessen, which covers a method for producing molecular polynitrogens.

Peer review information

Nature thanks Chunlin He, Thomas Klapötke and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions