Scientists Unveil Game-Changing Satellite Mega-Constellation Design

A new satellite constellation design method achieves global Earth observation within 35 minutes using optimized configurations of basic and accompanying satellites in LEO mega constellations.

A novel LEO constellation design uses grouped satellites and swarm optimization to achieve precise Earth observation, validated by simulation with 891 satellites.

Satellite constellations have long supported everything from GPS navigation to global internet and space-based reconnaissance. Well-known systems like GPS, Glonass, Beidou, and Starlink rely on fleets of satellites working together to provide seamless coverage. Now, the next generation of Low Earth Orbit (LEO) mega constellations is set to revolutionize how we observe Earth and develop cutting-edge satellite technology.

But designing these massive constellations isn’t easy. It’s a highly complex, nonlinear problem that traditional analytical methods struggle to solve. In the early days, the goal was simple: ensure satellites offered uniform coverage around the planet. Today, however, constellation design must meet the demands of specialized applications like high-resolution Earth imaging and rapid data transmission.

A recent study published in Space: Science & Technology offers a promising new solution. Researchers from Harbin Engineering University, the China Academy of Space Technology, and Stevens Institute of Technology have introduced an innovative method for designing LEO mega constellations. Their approach focuses on coordinating the orbits of both core and supporting satellites, allowing for smarter, more flexible configurations.

The team’s method takes into account key factors like imaging swath width, synchronized formation flying among satellite subgroups, and balanced global coverage using onboard instruments.

Defining satellite groups for optimized global coverage

The researchers began by dividing the fleet into two types: basic satellites and accompanying satellites. Each basic satellite is surrounded by a small group of accompanying satellites, and these satellite groups are evenly spaced around the Earth. All basic satellites follow the same ground path, known as a subsatellite trajectory, ensuring consistent global coverage.

Each of these clusters, made up of a basic satellite and its companions, forms what the researchers call a satellite group. The entire constellation is then built by repeating this group structure many times around the planet.

To calculate the optimal orbits for these basic satellites, the researchers used a model based on what’s known as a regression orbit. This involves finding the precise altitude (called the semimajor axis) where a satellite completes exactly R orbits around Earth in D days. They also accounted for natural gravitational effects, like Earth’s slightly uneven shape, to keep the satellites’ orbits stable over time.

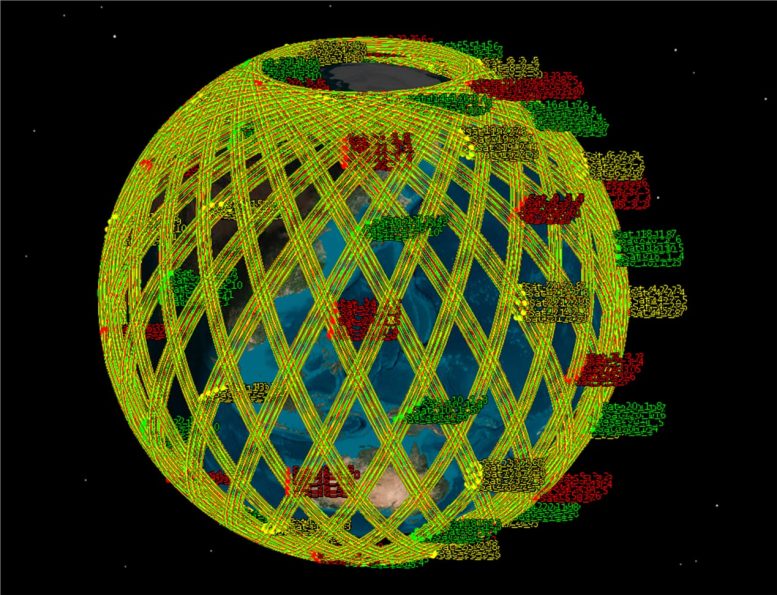Final LEO mega constellation configuration. Credit: Space: Science & Technology

Next, the team looked at how wide each satellite group can scan the Earth’s surface, which determines how many orbital paths are needed to cover the entire globe. They calculated this using Earth’s radius and the scanning width, ensuring no region is left out.

Finally, they considered how quickly satellites need to respond to observation requests. If users require images or data within a certain time, the satellites must be arranged so that at least one is always nearby. This helped them determine how many basic satellites are needed in each orbital path.

By combining all these factors — orbital height, timing, satellite spacing, and coverage — the researchers created a detailed method for designing high-performance mega constellations.

Designing elliptical trajectories for accompanying satellites

As for accompanying satellites, they have the semimajor axis with basic satellites. According to the Clohessy-Wiltshire equation, the relative motion trajectory between the basic satellites and the accompanying satellites is an ellipse. Then, considering that the position vectors at the initial time and T/2 relative to the basic satellite is oppositive, the orbital elements of the first accompanying satellites can be solved.

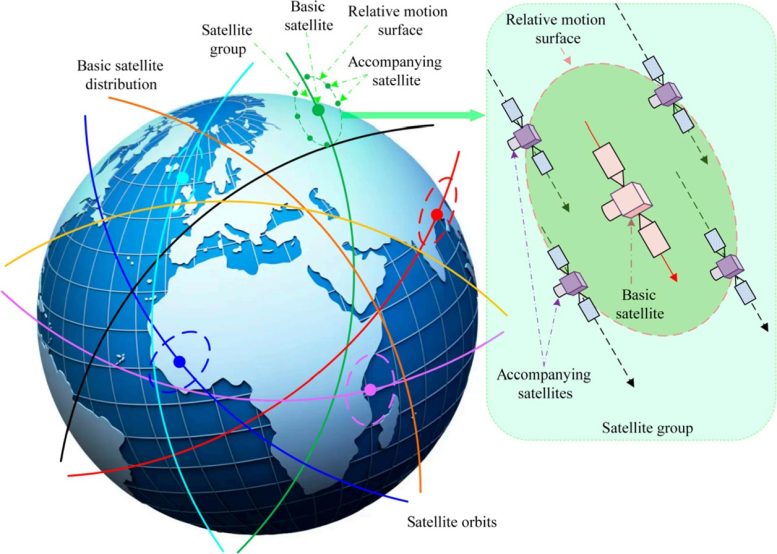Orbital distribution of LEO mega constellation. Credit: Space: Science & Technology

Assuming that the imaging width of a single satellite is sd, the number of accompanying satellites in a satellite group is N_a = ceiling(d/sd – 1). Divide the trajectory of the first accompanying satellite relative to basic satellite orbital coordinate system in chronological order, extract the position vectors of all equal points under the orbital system, and use these as the position vectors of other accompanying satellites under the basic satellite orbital system at initial time.

Combining the basic and accompanying satellites’ orbits, the configuration of mega constellation is obtained.

Applying optimization algorithms to refine configurations

Then, the orbit parameters of satellite and its companions are set as initial values, and the precise orbits under the High Precision Orbit Propagator model are solved in the neighborhood by using the Nondominated Sort Particle Swarm Optimization algorithm. Transform the orbital elements of any basic satellite into position and velocity information, which is recorded as {px_pq, py_pq, pz_pq, vx_pq, vy_pq, vz_pq}. Add an increment to build their neighborhood, which can be expressed to {Δpx_pq, Δpy_pq, Δpz_pq, Δvx_pq, Δvy_pq, Δvz_pq}.

The optimization variable of accompanying satellite orbit is the position and velocity increment of all basic satellites. The optimization objective f₁ for the basic satellite configuration is to minimize the absolute difference between the ascending and descending nodes of any basic satellite bs_pq in cycle i, and the ascending and descending nodes of bs_1q as much as possible. The optimization objective f₂ of the accompanying satellite is to keep the relative position as close as possible under the basic satellite orbit system at multiple subsequent motion periods. Optimization iteration process involves continuously approaching the Pareto front. In practice, find all nondominant solutions of the initial individual as the optimal solution set.

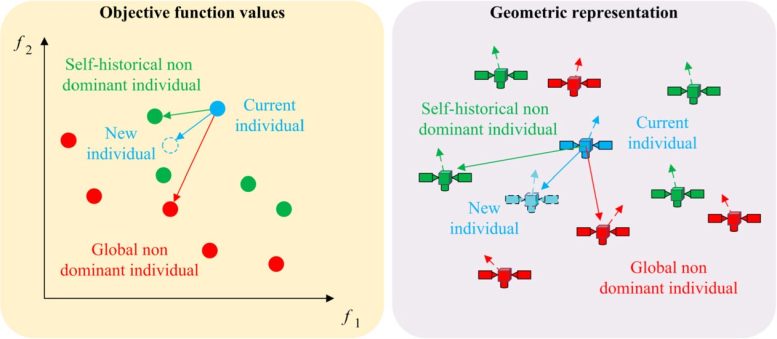Individual update process. Credit: Space: Science & Technology

Calculate 2 optimization objectives of everyone in sequence, and use the nearest global nondominated individual and own historical nondominated individual as learning objects. Update individual optimization variables and variable increments based on population information, individual experience, and self-inertia, as shown in Fig. 10. Then calculate the f₁ and f₂ of newly generated individuals again, and regenerate the global Pareto front and individual historical Pareto front.

After a fixed number of cycles or objective function is less than the threshold, the iteration ends and the global Pareto front can be obtained. At this point, the final constellation configuration can be selected based on user preferences or linear superposition of f₁ and f₂.

Finally, the correctness of the configuration design method is verified by numerical simulation. In the simulation, set the constellation orbital inclination as 66°, eccentricity as 0, argument of perigee as 0, simulation time as 1 d, set regression coefficient Q = 15, initial ascending node as 0, initial MA as 0, imaging width of a satellite group as 1500 km, imaging width of single satellite as 140 km, and maximum working time of single satellite to orbit single circle as 35 min. During the optimization, it can be observed that the approximation speed of the Pareto front in the first 100 generations is extremely fast.

As the number of iteration increases, the variation of the Pareto front gradually decreases and eventually becomes stable. In the final generation of nondominated solutions, we select the individual of f1 = 1.981 and f2 = 9516.482 as the final solution, and the constellation configuration is shown in Fig. 15. The constellation has a total of 891 satellites, of which 81 basic satellites are evenly distributed, with 10 accompanying satellites evenly distributed around each basic satellite. A total of 810 accompanying satellites can achieve collaborative observation of any position outside the polar region within 35 min.

Reference: “Configuration Design Method of Mega Constellation for Low Earth Orbit Observation” by Yuheng Yang, Xiande Wu, Jiamin Li, Jie Zang, Jianchun Lu and Ralf Zgeib, 18 June 2024, Space: Science & Technology.
DOI: 10.34133/space.0175

Never miss a breakthrough: Join the SciTechDaily newsletter.