Background
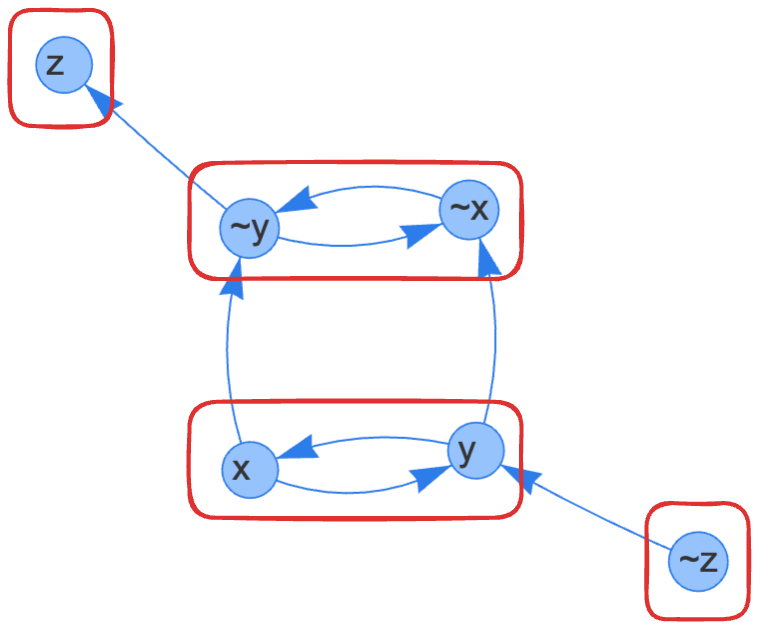
\[(x \lor \neg y) \land (\neg x \lor y) \land (\neg x \lor \neg y) \land (y \lor z)\]
While (SAT) is generally NP-complete, meaning no efficient algorithm is known to solve it for all cases, 2-SAT, a special case of SAT where each clause contains exactly two literals, can be solved efficiently in linear time!
Specifically, 2-SAT can be solved in O(n + m) time, where n is the number of variables and m is the number of clauses. involves
Algorithm
Implication Graph
Note that the expression \(a \lor b\) is equivalent to \((\neg a \Rightarrow b) \lor (\neg b \Rightarrow a)\), so the expression above is equivalent to: \[\begin{equation} \begin{aligned} (\neg x \Rightarrow \neg y \lor y \Rightarrow x) \lor (x \Rightarrow y \lor \neg y \Rightarrow \neg x) \lor (x \Rightarrow \neg y \lor y \Rightarrow \neg x) \lor (\neg y \Rightarrow z \lor \neg z \Rightarrow y) \end{aligned} \end{equation}\]
Now, we construct a graph, known as the Implication Graph, representing these implications.
http://jsfiddle.net/nim_a101/o5fj6snb/99/
Observations
- For every edge \(a \Rightarrow b\) , there is a corresponding edge \(\neg b \Rightarrow \neg a\).
- If \(a\) is reachable from \(\neg a\) and \(\neg a\) is also reachable from \(a\), the problem has no solution.
You can prove that the second observation is not just necessary but also sufficient for the expression to have a valid assignment.
Strongly Connected Components (SCCs)
Given the second observation from the previous section, we need to ensure no variable and its negative can reach each other (note that one reaching the other is not enough). In other words, for every variable we need to make sure \(a\) and \(\neg a\) are not in the same strongly connected component of the graph.
In order to find all SCCs of a graph we can utilize Kosaraju’s Algorithm. In short, the algorithm is as follows:
- find topological sort of nodes (using dfs)
- reverse all edges
- dfs from every unvisited node in reverse topological order to discover each SCC
Implementation
The algorithm is basically:
- Apply Kosaraju’s algorithm to find SCCs
- For each variable, ensure \(a\) and \(\neg a\) are not in the same SCC
Finding the Assignment
To find the actual assignment, if there’s a path between a variable and its negative:
- if \(a \leadsto \neg a\), we set \(a\) to true
- if \(\neg a \leadsto a\), we set \(a\) to false.
Note that the way Kosaraju’s algorithm works, if there is a path from node a to b, comp[a] >= comp[b] and since they are not in the same component, we would have comp[a] > comp[b].
Note: The implementation below leverages the fact that in python you can have negative indices in an array, where index -N means the N-th cell from the end. So we can store the first variable (say \(x\)) as 1 and the negative of it as -1 (and we won’t use the index 0).
Proof
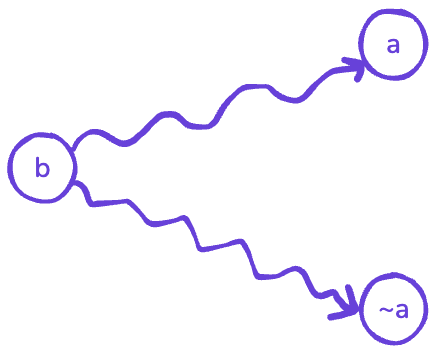
We mentioned that it’s necessary and sufficient to ensure \(a\) and \(\neg a\) are not in the same SCC. However, what if both \(a\) and \(\neg a\) can be reached from another variable \(b\)? Let’s prove by contradiction and suppose such situation exists.
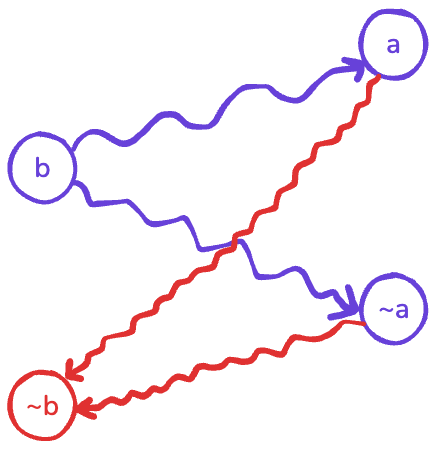
Note that given the first observation above, if this situation happens, we also know that \(\neg b\) is reachable from both \(a\) and \(\neg a\).
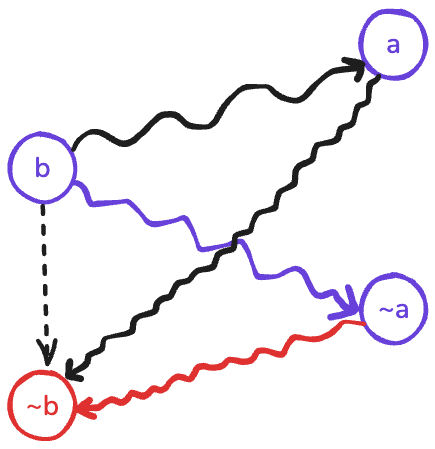
Now, using transitivity, \(\neg b\) should be reachable from \(b\) (and vice versa) which causes a contradiction.
.png)




