Solving LinkedIn Queens with APL

14 Jun 2025 on Peter Vernigorov’s blog

A couple months ago I noticed that LinkedIn now has a few simple games. They aren’t much to write home about, but I really enjoyed playing the Queens.

This week I saw two posts about solving the Queens game programmatically. They both are quite interesting reads for me, and I thought that this would be a good opportunity to also solve the game in my favourite language - APL - and share my experience. Having been using APL for Advent of Code, I wanted to share my passion for it with others.

Rules

The game is pretty straight forward: each colour region must have exactly one queen, and two queens cannot be on the same row, column, or next to each other. Multiple queens on the same diagonals are allowed, as long as they are separated by at least one space.

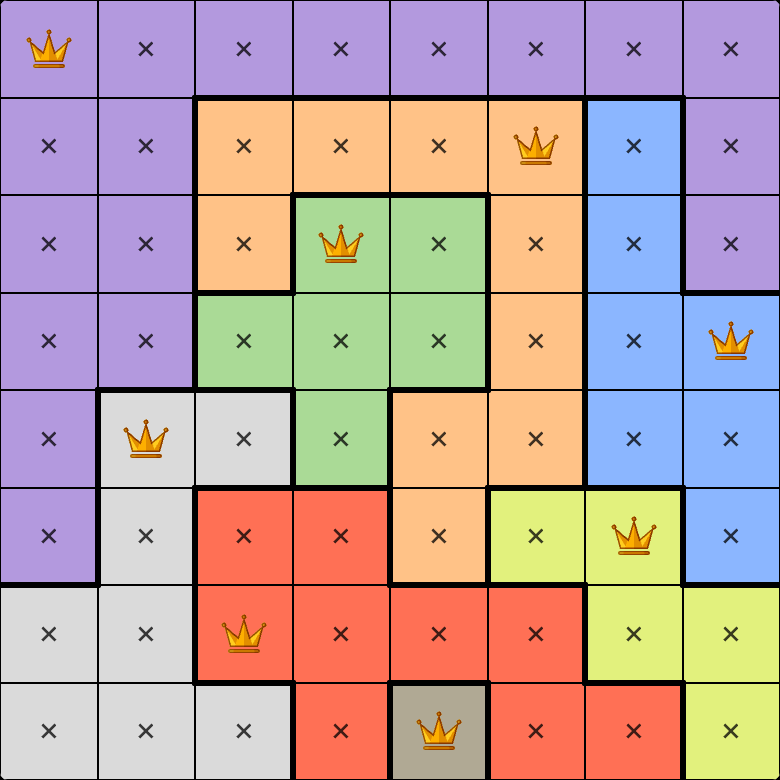
Board

First, let’s figure out the data structure. LinkedIn sends the initial state to the client as a list of rows, assigning each colour a number starting from 0. Well, that works just fine for APL, let’s create a 2 dimensional board representing above picture:

b←⍉⍪0 0 0 0 0 0 0 0 b⍪← 0 0 1 1 1 1 2 0 b⍪← 0 0 1 3 3 1 2 0 b⍪← 0 0 3 3 3 1 2 2 b⍪← 0 4 4 3 1 1 2 2 b⍪← 0 4 5 5 1 6 6 2 b⍪← 4 4 5 5 5 5 6 6 b⍪← 4 4 4 5 7 5 5 6

and print it (by assigning it to the screen represented by a box)

⎕ ← b 0 0 0 0 0 0 0 0 0 0 1 1 1 1 2 0 0 0 1 3 3 1 2 0 0 0 3 3 3 1 2 2 0 4 4 3 1 1 2 2 0 4 5 5 1 6 6 2 4 4 5 5 5 5 6 6 4 4 4 5 7 5 5 6

When actually solving the puzzle, I will use zero as a special value - location of queens - so in the solution I will increment all numbers by 1 using a simple b + 1 expression. But we are not there yet.

Breadth-first Search

Next, let’s decide on the algorithm. There are two usual options here, depth-first search and breadth-first search. While depth-first option is a somewhat obvious choice, and the demonstration of solving the classic N-queens problem was beautifully done in this video, in LinkedIn Queens I decided to go with breadth-first search. My solution is inspired by a sudoku solution video, it is one of my favourite approaches.

In our case, the depth of the search tree will be equal to the number of colours. At each step we will take the current solution space, and expand it by enumerating queen positions for a new colour. Here is a mock output that should help explain the algorithm using a simpler board (colour order is chosen strategically):

Let’s imagine we created an infix operator fills that takes a colour and current solution space, and produces a new solution space. We start with the board as an initial solution space, and fill colour 4 with 4 fills b. Since APL is executed right-to-left, we can then fill colour 3 with 3 fills 4 fills b. And so forth… the whole solution would be the result of 2 fills 1 fills 0 fills 3 fills 4 fills b.

For those familiar with functional programming, this will look like a use case for a fold, specifically foldr (right fold). In APL this is such a common operation that it is shortened to a single symbol - /. The above becomes fills / 2 1 0 3 4 b.

So far, we’ve been designing the solution using mock output and pseudo code. However, the top-level function for our actual solution will look very similar to the code we used, by first building that list and then folding it. In fact, here it is:

solve ← {0=⊃fills/(∪,1+⍵),⊂⊂1+⍵}

Let’s see how it works when built up slowly. Comments start with ⍝ symbol (a light bulb).

⍝ an anonymous function that just returns the argument ⍝ ⍵ is a symbol for right argument ⎕ ← {⍵} b 0 1 1 1 1 2 3 2 1 2 2 3 2 2 2 2 2 2 4 4 2 2 2 2 2 ⍝ increment by 1, remember that 0 will be a special value ⎕ ← {1+⍵} b 1 2 2 2 2 3 4 3 2 3 3 4 3 3 3 3 3 3 5 5 3 3 3 3 3 ⍝ flatten the board ⎕ ← {,1+⍵} b 1 2 2 2 2 3 4 3 2 3 3 4 3 3 3 3 3 3 5 5 3 3 3 3 3 ⍝ unique list of colours ⎕ ← {∪,1+⍵} b 1 2 3 4 5 ⍝ board again, incremented by 1 ⎕ ← {1+⍵} b 1 2 2 2 2 3 4 3 2 3 3 4 3 3 3 3 3 3 5 5 3 3 3 3 3 ⍝ enclosed twice, making a solution space with one boxed element ⎕ ← {⊂⊂1+⍵} b 1 2 2 2 2 3 4 3 2 3 3 4 3 3 3 3 3 3 5 5 3 3 3 3 3 ⍝ create a list that we will fold over as explained earlier ⎕ ← {(∪,1+⍵),⊂⊂1+⍵} b 1 2 3 4 5 1 2 2 2 2 3 4 3 2 3 3 4 3 3 3 3 3 3 5 5 3 3 3 3 3 ⍝ actually fold using our fills operator ⎕ ← {fills / (∪,1+⍵),⊂⊂1+⍵} b 0 2 2 2 2 3 4 3 0 3 3 0 3 3 3 3 3 3 5 0 3 3 0 3 3 ⍝ disclose twice ⎕ ← {⊃⊃fills/(∪,1+⍵),⊂⊂1+⍵} b 0 2 2 2 2 3 4 3 0 3 3 0 3 3 3 3 3 3 5 0 3 3 0 3 3 ⍝ pretty print the result ⎕ ← {'♕0123456789'[⍵]} {0=⊃⊃fills/(∪,1+⍵),⊂⊂1+⍵} b ♕ 1 1 1 1 2 3 2 ♕ 2 2 ♕ 2 2 2 2 2 2 4 ♕ 2 2 ♕ 2 2

Fleshing out details

Now we are ready to actually implement the fills function. But first let’s define some helpers.

The first helper is a place function that places a 0 (queen) on the board. It’s called like this: 1 2 place b. We will use an At operator, represented by symbol @:

⍝ ⍺ is the left argument place ← {0@(⊂⍺)⊢⍵} ⎕ ← 5 5⍴1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ⎕ ← 1 2 place 5 5⍴1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

Easy enough!

Note: APL allows overriding index origin. The default is 1-based; however, the place function doesn’t work there for surprisingly complicated reasons - it involved the behaviour of Each with empty lists, prototypes, and @ primitive failing when asked to update index (0,0) in 1-based origin system. So this function assumed that the origin is setup with ⎕IO ← 0. The rest of the code doesn’t care about index origin.

Now, let’s build the function - we will call it avl - that returns actually available queen positions for a specific colour. It will exclude positions that are invalid. We will call it with colour and board as such - 4 avl b

avl ← { ⍝ find positions of all existing queens q ← ⍸0=⍵ ⍝ find positions of a particular colour p ← ⍸⍺=⍵ ⍝ boolean mask over p that have row or column conflict with any existing queen rc ← ∨⌿1∊¨q∘.=p ⍝ boolean mask over p that are next to any existing queen nx ← ∨⌿∧/¨1≥|q∘.-p ⍝ select colour positions that are covered by neither mask using a nor ⍝ here slash symbol is a select, not fold (rc⍱nx)/p }

Last line in this function implicitly returns the result - list of legal positions for a queen in the colour region. I leave deeper understanding of this function as an exercise to the reader. For those unfamiliar with APL primitives, APL Wiki has great pages for each, such as ⍸ - indices function.

And now we are ready to implement the fills function. We will split it into two functions - fills that works on a solution space and fill that works on a single instance of a board. Left argument for both is always the colour.

⍝ places a queen on each available position of a board fill ← {(⍺ avl ⍵) place¨ ⊂⍵} ⍝ calls fill for each board, then merged the results fills ← {⊃,/⍺ fill¨ ⍵}

And that’s it!

The code

The whole solution is this:

place ← {0@(⊂⍺)⊢⍵} avl ← { q ← ⍸0=⍵ p ← ⍸⍺=⍵ rc ← ∨⌿1∊¨q∘.=p nx ← ∨⌿∧/¨1≥|q∘.-p (rc⍱nx)/p } fill ← {(⍺ avl ⍵) place¨ ⊂⍵} fills ← {⊃,/⍺ fill¨ ⍵} solve ← {⊃⊃fills/(∪,1+⍵),⊂⊂1+⍵}

11 lines of code that have zero external dependencies, not even APL’s built-in libraries. Just the primitives. avl can be minified to much fewer lines, but I see no reason to do that.

There are heuristics that could be used, such as ordering colours by number of positions (fill smaller regions first). However, the current solution runs in a few milliseconds already. Still, there might be edge case boards where this solution doesn’t perform well, but I do not have many data points.

Let’s solve the large example:

⎕ ← board 0 0 0 0 0 0 0 0 0 0 1 1 1 1 2 0 0 0 1 3 3 1 2 0 0 0 3 3 3 1 2 2 0 4 4 3 1 1 2 2 0 4 5 5 1 6 6 2 4 4 5 5 5 5 6 6 4 4 4 5 7 5 5 6 ⎕ ← solve board ♕....... .....♕.. ...♕.... .......♕ .♕...... ......♕. ..♕..... ....♕...

The End

My hope is that this has piqued your interest in APL, at least from the perspective of expanding your programming toolbox. APL is a very powerful language that allows you to express complex algorithms in a very concise way. If you want to learn more, I recommend checking out APL Wiki and TryAPL.

---

Discussion: https://lobste.rs/s/9gjyi0