Techniques to beat Arrays.hashCode(byte[]) using Java's own means

Java’s Arrays class provides a utility function to compute a 32-bit hash value for a given byte[] array. The function was introduced in Java 1.5, and therefore, one could assume that its implementation has been highly optimized in the meantime. So, it is astonishing that we still found faster pure Java implementations beating the default and the intrinsic implementations of OpenJDK 24.

Definition of Arrays.hashCode(byte[])

Arrays.hashCode(byte[]) is a very simple method that computes the hash code for a given byte[] array with elements b[0], b[1], …, b[n−1] using the recursion

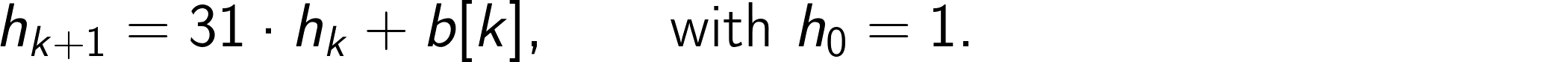
The method was implemented up to OpenJDK 20 as

static int hashCode(byte[] b) {    if (b == null) return 0;    int h = 1;    for (byte q : b) {      h = 31 * h + q;    }    return h;  }

The iterative processing of individual bytes does not allow for many compiler optimizations. However, following Professor Daniel Lemire’s idea described in his blog “Faster hashing without effort,” some speedup can be achieved by unrolling the loop and reducing the data dependency. For example, unrolling eight steps gives:

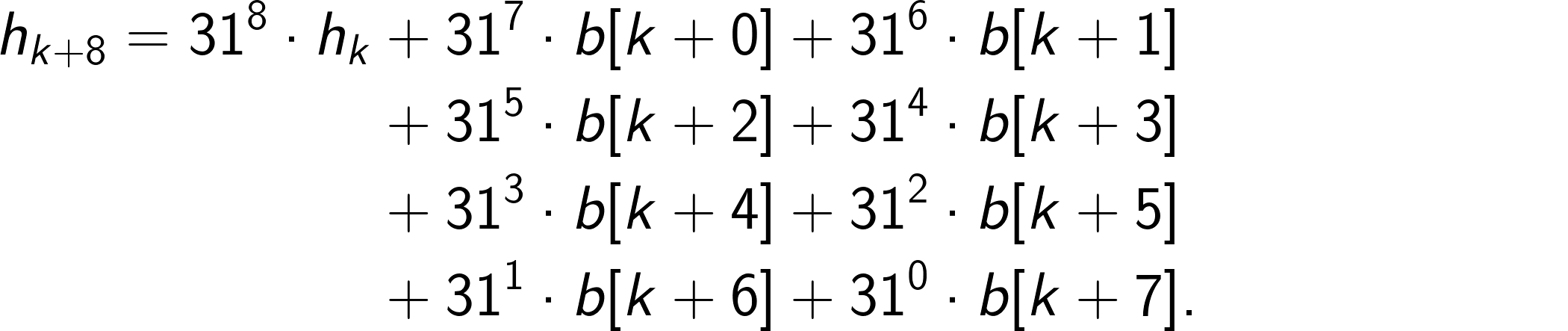
The powers of 31 would be precomputed and replaced by corresponding constants. However, for further acceleration, we have to process multiple bytes in parallel, also known as vectorization.

Modern CPUs can apply a single instruction simultaneously to multiple data (SIMD). Moreover, with some tricks, it is sometimes even possible to realize SIMD within a single CPU register, also known as SIMD within a register (SWAR). We leveraged both techniques to develop two new alternative implementations of Arrays.hashCode(byte[]). Before we describe them in more detail, let’s first look at the benchmark results.

Benchmark results

The different implementations, including the source code for the JMH benchmark, can be found on GitHub. The benchmark was executed on an AWS c5.metal instance running Ubuntu 24.04 with disabled Turbo Boost (P-state set to 1) and using OpenJDK 24.0.1. We measured the average runtime for computing the hash code for different sets of byte arrays. Each set consists of 10,000 random byte arrays. To make the execution path unpredictable and to prohibit unwanted compiler optimizations, the lengths are randomly chosen from the range [0, L]. The maximum byte array length L is a benchmark parameter, which we varied from 1 up to 10⁵.

Our main baselines are the two OpenJDK implementations, the default Java implementation, and the intrinsic implementation. The latter was introduced with OpenJDK 21 and utilizes SIMD CPU instructions. The default implementation was tested by disabling the intrinsic implementation by adding the following JVM arguments:

-XX:+UnlockDiagnosticVMOptions -XX:DisableIntrinsic=_vectorizedHashCode

Additionally, we considered manual loop unrolling as described above, which is already faster than the default implementation. The results are summarized in the following figure, showing the average runtime over the maximum byte array length L.

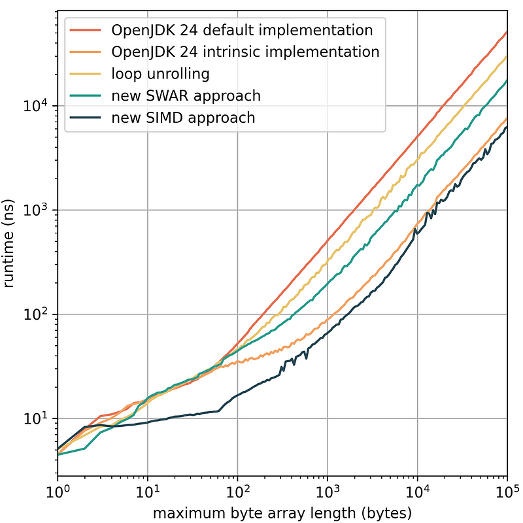
Our new SWAR-based implementation is up to 2.9x faster than the default implementation and also significantly better than loop unrolling. Even though the intrinsic implementation already reduces the runtime by almost an order of magnitude compared to the default implementation, it is less performant than our SIMD-based Java implementation using the Vector API. In the following, we describe in detail how we achieved these performance gains with pure Java code only. Let’s start with the SWAR-based solution.

The SWAR approach

Since 8 bytes perfectly fit into a 64-bit long integer, we aim at processing 8 bytes at once. Since Java 9, there has been a fast and convenient way to load multiple bytes from the byte[] array into a long variable using a VarHandle, as shown by the following code snippet.

static final VarHandle VAR_HANDLE =      MethodHandles.byteArrayViewVarHandle(long[].class, ByteOrder.LITTLE_ENDIAN);    static long getLong(byte[] b, int k) {    return (long) VAR_HANDLE.get(b, k);  }

This code transforms 8 bytes into a long, assuming little-endian, which means the first byte of the array defines the least significant 8 bits of the long value. Enforcing little-endian byte order might not be the fastest approach on big-endian architectures. However, all the tricks described below can be adapted for big-endian.

Rewriting the recursion

The above unrolled recursion can be equivalently written as follows:

At first glance, this expression looks much more complicated. However, it has a couple of benefits:

1. There are 4 multiplications with a factor of 31, and 2 multiplications with the same factor of 31², which are candidates to be performed in a vectorized fashion.
2. Bytes in Java are signed and, therefore, always in the range [−128, 127]. Adding 128 maps them to the range [0, 255], which makes the multiplications unsigned. To compensate for that, we need to deduct the last term, which is constant and can be precomputed. Adding 128 to every byte is also a candidate for vectorization.

Computing a single recursion step

When introducing the following constants

static final int P2 = 31 * 31; // P2 = 31^2  static final int P4 = P2 * P2; // P4 = 31^4  static final int P8 = P4 * P4; // P8 = 31^8    // U = -128 * (31^7 + 31^6 + 31^5 + 31^4 + 31^3 + 31^2 + 31 + 1)  //   = -128 * (1 + 31) * (1 + 31^2) * (1 + 31^4)  static final int U = -128 * (1 + 31) * (1 + P2) * (1 + P4);

the recursion formula above can be implemented in Java using the following lines of code, which are explained in the following:

long x = getLong(b, k) ^ 0x8080808080808080L;  x = 31 * (x & 0x00FF00FF00FF00FFL) + ((x >>> 8) & 0x00FF00FF00FF00FFL);  x = P2 * (x & 0x0000FFFF0000FFFFL) + ((x >>> 16) & 0x0000FFFF0000FFFFL);  h = P8 * h + P4 * (int) x + (int) (x >>> 32) + U;

Line 1

The first line loads 8 bytes into a long variable and applies an XOR operation with 8080808080808080₁₆, which flips the most significant bits of each of the 8 bytes, equivalent to adding 128. For example, a byte with binary value 10100111₂ interpreted as a signed value would correspond to −89. If we flip the first bit, we would get 00100111₂. Interpreted as an unsigned value, this corresponds to −89 + 128 = 39. After processing the first line, the individual bytes of variable x are equal to
(b[k+7] + 128, b[k+6] + 128, …, b[k+0] + 128).
The XOR operation is the first SWAR operation, performing eight additions with a single CPU instruction.

Line 2

The second line masks every second byte using 00FF00FF00FF00FF₁₆, which gives

(0, b[k+6] + 128, 0, b[k+4] + 128, 0, b[k+2] + 128, 0 , b[k+0] + 128).

The multiplication of this long value with 31 actually carries out the four multiplications of 31 with

(b[k+6] + 128), (b[k+4] + 128), (b[k+2] + 128), (b[k+0] + 128)

with a single CPU instruction. Since the products are limited by 31 · 255 = 7905 <2¹⁶  and therefore fit into 2 bytes, the individual multiplications will not interfere with each other. After this step, we have the values

(b[k+6] + 128) · 31, (b[k+4] + 128) · 31,
(b[k+2] + 128) · 31, (b[k+0] + 128) · 31

in 2 bytes of the resulting long value each. Right shifting by 8 bits and again masking with 00FF00FF00FF00FF₁₆ yields the values

(b[k+7] + 128), (b[k+5] + 128), (b[k+3] + 128), (b[k+1] + 128),

also represented by two bytes of a long each. Summation with the result of the multiplication results in having the values

((b[k+7] + 128) + (b[k+6] + 128) · 31),
((b[k+5] + 128) + (b[k+4] + 128) · 31),
((b[k+3] + 128) + (b[k+2] + 128) · 31),
((b[k+1] + 128) + (b[k+0] + 128) · 31)

in 2 bytes of x each. As these values can still be represented by 2 bytes, the four parallel summations are carry-free and don’t interfere.

Line 3

The third line applies the same trick as line 2 to perform the two multiplications with P2 = 31² in parallel. After this step, x will contain the value of

((b[k+7] + 128) + (b[k+6] + 128) · 31) + ((b[k+5] + 128) + (b[k+4] + 128) · 31) · 31²

in the most significant 4 bytes and that of

((b[k+3] + 128) + (b[k+2] + 128) · 31) + ((b[k+1] + 128) + (b[k+0] + 128) · 31) · 31² 

in the least significant bytes of x.

Line 4

The fourth line completes the recursion by multiplying the previous value of h by 31⁸, adding the product of the least significant 4 bytes of x with 31⁴, adding the most significant 4 bytes of x (obtained via right shifting by 32 bits and casting to an int), and adding the precomputed constant U.

The final SWAR implementation

The recursion always processes 8 bytes at once. If the length of the byte array is not divisible by 8, we have to treat the remaining bytes differently. The following code summarizes the new SWAR-based hash code computation

static int hashCodeSWAR(byte[] b) {    if (b == null) return 0;    if (b.length == 0) return 1;    if (b.length == 1) return 31 + b[0];    int h = 1;    int k = 0;    for (; k <= b.length - 8; k += 8) {      long x = getLong(b, k) ^ 0x8080808080808080L;      x = 31 * (x & 0x00FF00FF00FF00FFL) + ((x >>> 8) & 0x00FF00FF00FF00FFL);      x = P2 * (x & 0x0000FFFF0000FFFFL) + ((x >>> 16) & 0x0000FFFF0000FFFFL);      h = P8 * h + P4 * (int) x + (int) (x >>> 32) + U;    }    return finalize(h, b, k);  }

where the finalize function handles the remaining bytes (up to 7). In our experiments, this unrolled version was faster than any loop.

static int finalize(int h, byte[] b, int k) {    if (k < b.length) {      h = 31 * h + b[k++];      if (k < b.length) {        h = 31 * h + b[k++];        if (k < b.length) {          h = 31 * h + b[k++];          if (k < b.length) {            h = 31 * h + b[k++];            if (k < b.length) {              h = 31 * h + b[k++];              if (k < b.length) {                h = 31 * h + b[k++];                if (k < b.length) h = 31 * h + b[k];              }            }          }        }      }    }    return h;  }

The SIMD approach

SIMD instructions can be directly accessed via Java’s Vector API, which has been available as an incubator module since Java 16. Löff et al. recently showed in their work “Vectorized Intrinsics Can Be Replaced with Pure Java Code without Impairing Steady-State Performance” that the Vector API allows achieving similar performance as intrinsic native implementations. Our SIMD-based solution additionally uses some tweaks to actually undercut the performance of the intrinsic implementation, in particular for mid-sized byte arrays.

Rewriting the recursion

The original recursion formula starts with h₀ = 1. Since SIMD registers are easier to initialize with zero, we introduce

to transform the recursion into

As for the SWAR approach, problems with negative values can be avoided by writing the recursion as

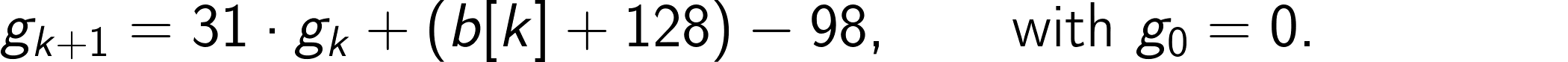
Now we unroll L steps of this recursion, where L is the SIMD register width in bytes:

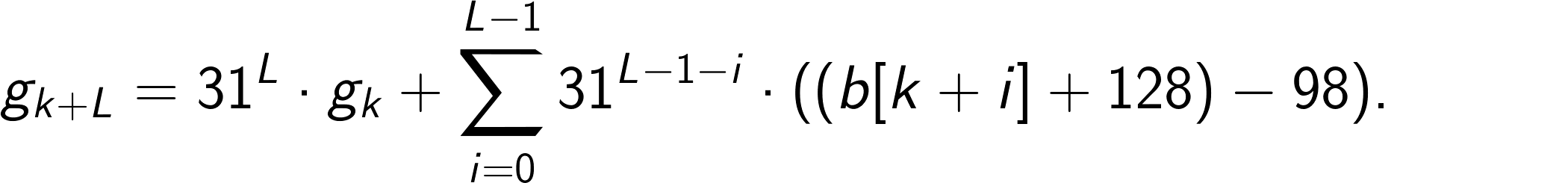
For 512-bit registers, for example, we would have L = 64.

Vectorized computation

If k is a multiple of L, which again is a multiple of 4, we can also write gₖ as the linear combination

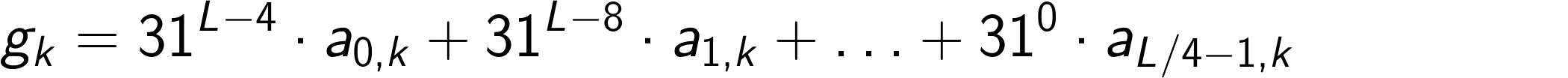
where the sequences a_r,k are given by

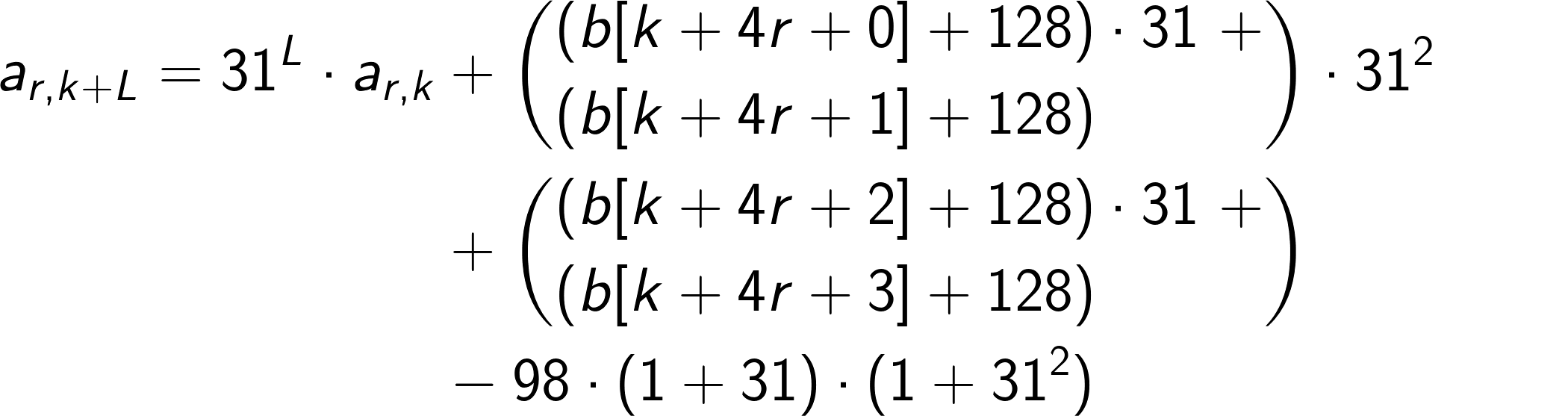
with

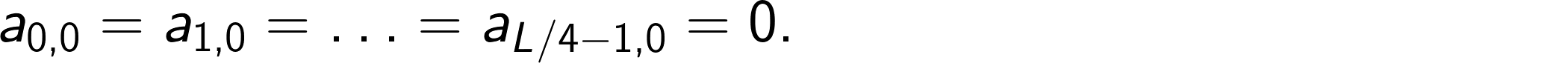
If a is a variable of type IntVector able to represent L/4 32-bit integers, a single iteration step can be computed simultaneously for L/4 subsequent elements of this sequence by the following Java code using the Vector API:

a = a.mul(PL); // PL = 31^L  var s = ByteVector.fromArray(ByteVector.SPECIES_PREFERRED, b, k)          .lanewise(XOR, (byte) 0x80) // add 128          .reinterpretAsShorts();  var i = s.and((short) 0xFF)          .mul((short) 31)          .add(s.lanewise(LSHR, 8))          .reinterpretAsInts();  a = a.add(i.and(0xFFFF).mul(P2).add(i.lanewise(LSHR, 16))); // P2 = 31^2  a = a.add(V); // V = -98 * (1 + 31) * (1 + 31^2)

The first line performs the multiplication with 31ᴸ. Then, similar to the SWAR approach, all bytes are XORed with 80₁₆, which corresponds to adding 128. Next, the L bytes are reinterpreted as L/2 short values. The least significant bytes are multiplied by 31, and the corresponding most significant bytes are added. This is repeated analogously after reinterpreting the L/2 short values as L/4 integer values. The least significant 2 bytes multiplied by 31² are added to the most significant 2 bytes. Finally, the constant V is added.

Computing the hash value

If the byte array length is a multiple of L, the final hash value h can be simply obtained by evaluating the linear combination and adding 1 according to

// W = {31^(L-4), 31^(L-8), ..., 31^4, 31^0}  int h = 1 + a.mul(W).reduceLanes(ADD);

where W is a vector containing the precomputed coefficients of the linear combination.

If the array length is not a multiple of L, we pad the byte array with zeros such that the effective length is again a multiple of L. Of course, this will lead to a different hash code. According to the recursive definition, every extra zero byte multiplies the hash code by 31. For example, if we had to pad the byte array with five zeros, the hash code would be wrong by a factor of 31⁵. Since 31 is odd, we can use its modular multiplicative inverse with respect to 32-bit integer arithmetic, which is

static final int I = 0xbdef7bdf;

The multiplication by I inverts the multiplication by 31 because I multiplied by 31 results in 1. Hence, in our example, if the hash code is wrong by a factor of 31⁵, we just have to multiply it by I⁵. Since L limits the maximum number of padded zeros, all necessary powers of I can be precomputed and stored in an array. Therefore, we only need an array lookup and an integer multiplication to fix the hash code computation after padding with zeros.

The final SIMD implementation

Putting everything together gives the final algorithm based on the following Java Vector API:

static int hashCodeSIMD(byte[] b) {    if (b == null) return 0;    if (b.length == 0) return 1;    if (b.length == 1) return 31 + b[0];    var a = IntVector.zero(IntVector.SPECIES_PREFERRED);    int remaining = b.length;    int k = 0;    while (remaining > L) {      var s =          ByteVector.fromArray(ByteVector.SPECIES_PREFERRED, b, k)              .lanewise(XOR, (byte) 0x80)              .reinterpretAsShorts();      var i = s.and((short) 0xFF)              .mul((short) 31)              .add(s.lanewise(LSHR, 8))              .reinterpretAsInts();      a = a.add(i.and(0xFFFF).mul(P2).add(i.lanewise(LSHR, 16)));      a = a.add(V);      a = a.mul(PL);      k += L;      remaining -= L;    }    return finalizeSIMD(a, b, k, remaining);  }

and finalizeSIMD is defined as

static int finalizeSIMD(IntVector a, byte[] b, int k, int remaining) {    var s =        ByteVector.fromArray(                ByteVector.SPECIES_PREFERRED,                b,                k,                ByteVector.SPECIES_PREFERRED.indexInRange(0, remaining))            .lanewise(XOR, (byte) 0x80)            .reinterpretAsShorts();    var i = s.and((short) 0xFF)            .mul((short) 31)            .add(s.lanewise(LSHR, 8))            .reinterpretAsInts();    a = a.add(i.and(0xFFFF).mul(P2).add(i.lanewise(LSHR, 16)));    a = a.add(V);    return (1 + a.mul(W).reduceLanes(ADD))               * F[remaining]; // F[remaining] = I^(L - remaining)  }

and F is the array that stores the precomputed powers of I that are needed to compensate for the padded zeros.

Conclusion: Faster implementations of Arrays.hashCode(byte[])

We have presented two alternative pure Java implementations for Arrays.hashCode(byte[]) based on SWAR and SIMD techniques, respectively. The SWAR approach is superior to the default Java implementation of OpenJDK 24.0.1, and our SIMD-based implementation utilizing Java’s Vector API beats OpenJDK’s intrinsic implementation. Based on these findings, we can conclude that the current OpenJDK implementations are not optimal and could be improved in the future by adopting some of the presented techniques.

Links

• Dynatrace Research GitHub repository
• Blog: Faster hashing without effort by Daniel Lemire
• Research article: Vectorized Intrinsics Can Be Replaced with Pure Java Code without Impairing Steady-State Performance by Löff, Schiavio, Rosà, Basso, and Binder