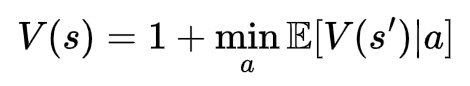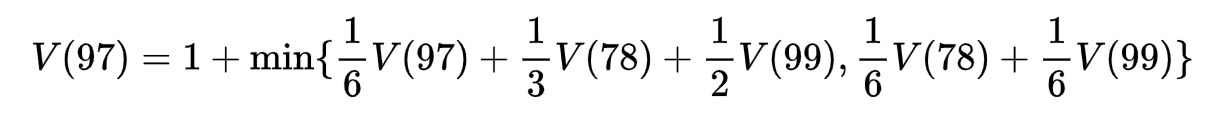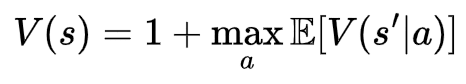If you go up into your parents’ attic and dust off some boxes, you might find, hidden amongst the memorabilia of a simpler time, a game called Snakes and Ladders (or sometimes Chutes and Ladders). The game originated in ancient India and was called Moksha Patam with a simple goal: to get from the bottom of the board to the top, moving through the squares sequentially using a die. But when you land on a square at the bottom of a ladder, you get to instantly climb it and move to the connecting square on the other end. And similarly, landing at the top of a snake means you slide down the snake from its mouth to its tail.

In the 1890’s the game was brought to Britain, where it was transformed into a moralistic exercise about virtue and the temptations of sin (the British unable to resist the obvious serpent allusion staring them in the face). Gameplay wise, it’s pretty simple, and it’s mainly used to pass the time and teach children about how to roll dice and move small tokens around, while dealing with success and failure gracefully. In my experience it’s fun to play a couple of times until quickly realizing there’s absolutely no skill or decision-making involved. Perhaps it’s a clever metaphor for life or the determinism of our environment. It evokes questions of meaning especially when analyzed from a traditionally Christian viewpoint; what does it mean for us to make “good” decisions in life in the context of an omniscient God? Are we puppets of circumstances or do we have true free will? Elements of being that are even hidden from an all knowing creator? Wouldn’t that violate the principle of omniscience, much less omnipotence?
Anyhow, let’s ruin your childhood and maybe your spirituality a bit today.
Snakes and Ladders seems pretty random at first glance, but there are some interesting patterns we can observe. The game can be modeled easily as a Markov Chain, which is just a fancy way of saying there are states that we can be in and transition to other states probabilistically. In this case a state is simply the square we’re on (let’s call this s) and if we roll a six sided dice it means we have a likelihood ⅙ of landing on the next square, (s+1), a likelihood ⅙ of landing at s+2, and so on until s+6. The one complication are the snakes and the ladders, which you can think of as collapsing states. In other words, looking at the image from the board above, There is no state 4, because it’s the bottom of a ladder that ends at space 14. So when you roll the die in the very beginning, your next six states are (1, 2, 3, 14, 5, 6) each with equal probability. Similarly, if you started from space 50, you have five possible next states with roll of the die (67, 52, 53, 54, 55), with 53 having a ⅓ likelihood instead of ⅙. This is because of the snake starting from 56 and going down to 53.
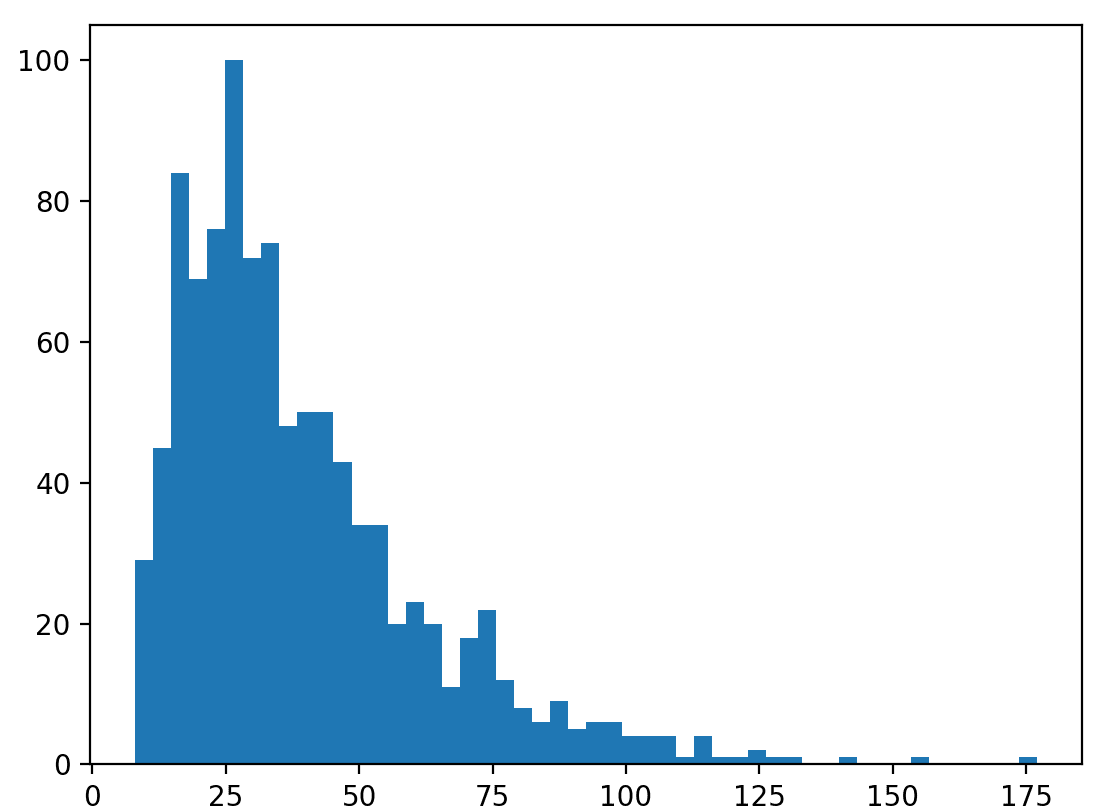
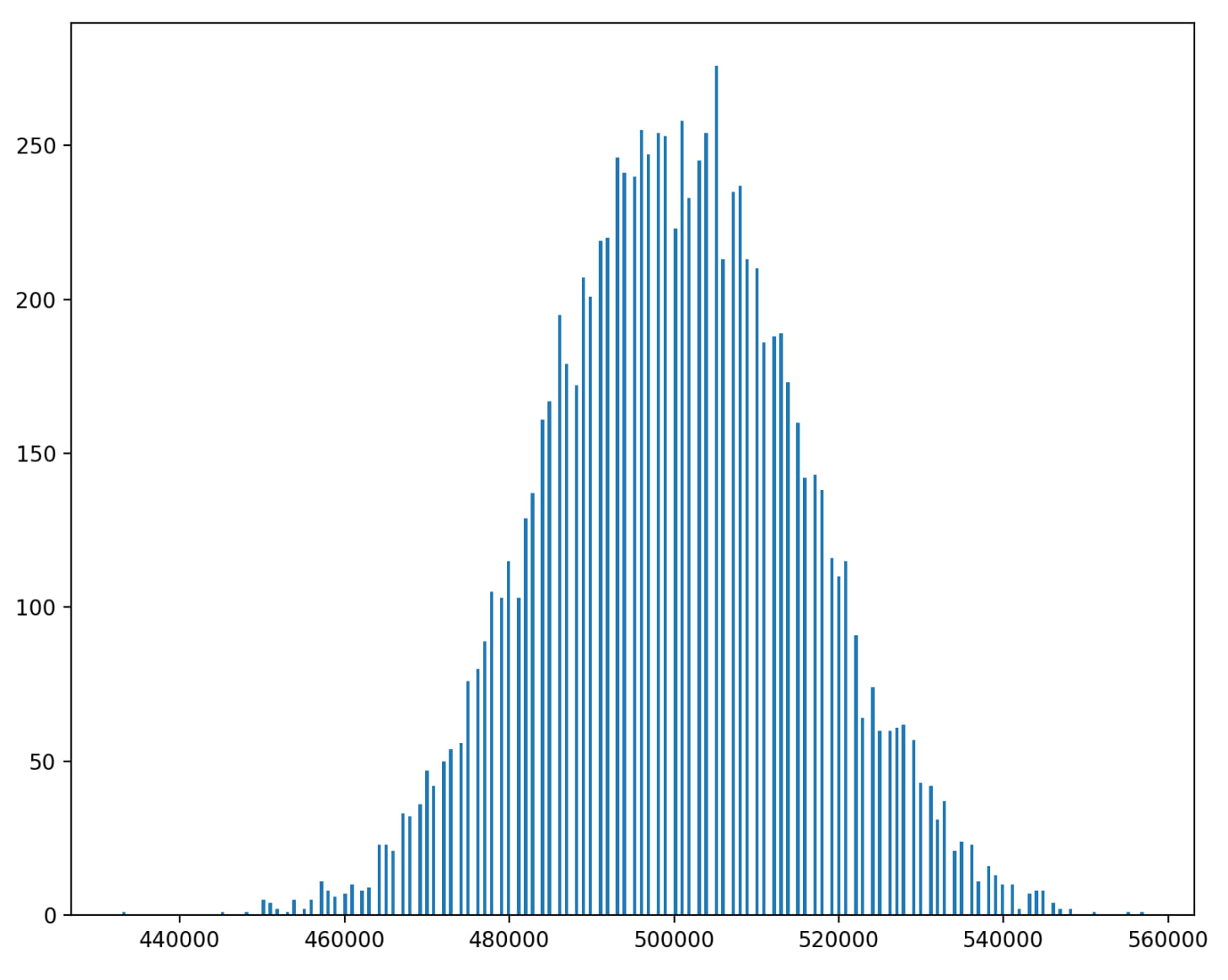
Now that we have a mathematical definition of the game, we can run a simulation of gameplay and see how long it takes for games to end. Below is a histogram of the length of games played for 1000 runs.
Although there are situations where a game can take a very long time (e.g. there’s a few games that took ~175 turns), most games end after about 30-40 turns. Technically a game could last forever (you might keep landing on that snake at space 98), but the likelihood of this is exceedingly low and the statistics of the game are relatively static.
This is somewhat interesting, but not particularly noteworthy. It reinforces the blind chance of the game and shows that a probabilistic process has an expected end time. Kind of like saying if you flip a coin enough times, eventually you’ll get 5 heads in a row. On average it might take 50 flips or so, but it could be an indefinitely long process with vanishing likelihood.
How can we make this game a little more interesting? How can we introduce some decision-making to the process?
Let’s add a new element to the game by introducing two new dice: a fast die, and a slow die. The fast die has 6 sides like a normal die, but its numbers are 4, 4, 4, 5, 5, and 6. This means rolling it will give you a ½ likelihood of getting a 4, a ⅓ likelihood of a 5, and a ⅙ likelihood of a 6. Think of it like a speedy die. The symmetric slow die has the numbers 0, 1, 1, 2, 2, 2, giving a ½ probability of a 2, ⅓ probability of a 1, and ⅙ probability of 0. Now the twist is that for each turn the player gets to pick which one out of the three dice (slow, normal, or fast) they use. What’s the best way to play this game?
The first question to make sure we have clarity on is: does it really matter which die you use? If we think about some situations in the game, we can see that this is most certainly the case. For example, if you’re at space 86, you certainly shouldn’t use the slow die. The slow die has a likelihood of getting a 1 with ⅓ which would result in a drop all the way down to space 24.
So between the options, would it be better to use the normal die or the fast die at space 86? Note that though the likelihood of a 1 is ⅓ for the normal die, it’s 0 for the fast die (because we don’t have a 1!). So all other things held equal, we should prefer to use the fast die at space 86. Now you might be wondering, is there a way we can mathematically capture this idea? And the answer of course is yes.
The idea we want to use here is expected value, a term avid poker players might already be familiar with. To illustrate it I’ll present you with a little game. Imagine you’re on a game show stage with a host displaying two boxes, one glass, and the other covered in cloth. The glass box displays $100 in plain sight, but before the show started, the host flipped a coin. If the coin came up heads, the host put $1,000,000 in the cloth-covered box. The game host offers you the options of picking the money in the glass box, or picking whatever is in the cloth covered box (either a million dollars, or absolutely nothing). What do you do? What should you do?
There might be some of you who pick the $100, maybe for a bit of a guarantee on some tangible prize, but I bet most of you would pick the cloth-covered box. After all, if the odds are actually 50-50, why not?
The host says: “Let’s take this a bit further” and removes the glass box from the stage. They now ask: “How much would you be willing to pay for opening the cloth covered box and taking what’s inside?”
Assuming there’s no chicanery and that you can trust the host flipped the coin and that the odds are truly even, how much would you pay? $1,000? $10,000? $500,000? In a one-off scenario like this it’s very hard to come up with a good answer. It depends a lot on your own personal finances and ability to handle risk more than just what the value of the box is. So the host offers you one more variant:
“I’m going to take out one thousand cloth-covered boxes. For each one I’ll flip a coin and put in $1,000 or nothing at all. I then take all of the money in all of the boxes and put it all in one very large cloth-covered box. How much would you pay for the very large box? You can certainly use any winnings from the box to pay for the original cost.”
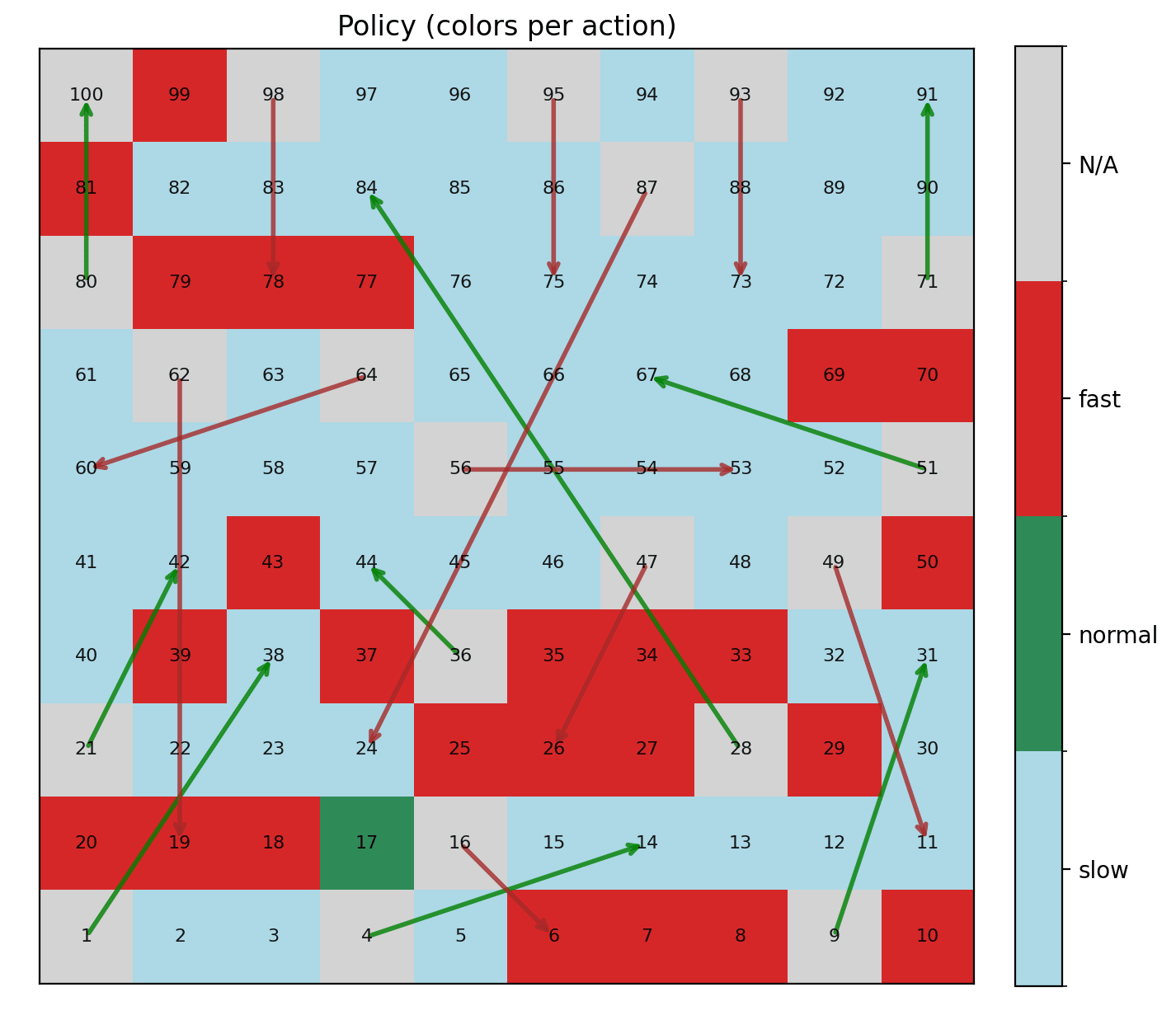
At the end of the day, the host still puts up to $1,000,000 of money into the box, but the situation feels very different. Instead of the money amount being either $0 or $1,000,000 with equal likelihood, it follows a distribution that peaks at $500,000. The likelihood of the amount of money in the box being exactly $500,000 is still quite low, but the likelihood of it being less than $400,000 is exceedingly low (i.e. less than 1 in a billion). Here is the game simulated for 10,000 runs:
Now how much would you pay? From a mathematical perspective, if we pay $400,000, our expected profit is $500,000 - $400,000 = $100,000. Seems like a no brainer.
Even though this is a purely probabilistic process, we can reason about good decision making and the fun piece is that there’s a natural way to map this idea of decision making in Snakes and Ladders with multiple dice.
In the same way that we could reason about the value of a box from the game show host problem above, we can also reason about the value of being at a square/space in the game of Snakes and Ladders. But instead of representing the expected amount of dollars, the value at a given square will represent something else: the expected number of rolls left in the game. We’ll use a value function V, which will provide the value for any given square. For example, the value at the very final square would be exactly 0 (because we’d be done with the game at this square and we don’t need to roll anymore). Therefore, V(100)=0.
But how do we calculate the other values? I propose we can represent the value function like so:
There’s a lot going on here so let’s break it down: The first piece to notice is the big E in the equation. This is an expectation operator, and all it’s really saying is to take the average of many new states we could end up in if we take an action a. In our case, an action “a” represents one of three options: the slow, normal, or fast die. We add 1 to this because it takes up one roll (and that’s what the value function is measuring).
It helps to work through an example: let’s calculate the value of space 97 using this formulation, but to keep it simple let’s just select between the normal and slow die. The fast die rolls 4 and above, and since we need to land on space 100 exactly to win it doesn’t actually help.
This equation makes a few simplifying assumptions:
The min operator is over using the slow die (the left part) or the normal die (the right part).
We don’t technically have a space 98 (the top of the snake), so we just encode this as state 78 directly.
We don’t include the V(100) term because it’s 0.
Take a guess: is it better to use the slow die or the normal die at space 97? You can check your answer in a little bit.
As it turns out, you can find the values of all of the squares using a technique called Value Iteration. The idea is to continually calculate the value function until it stops changing too much (i.e. reaches convergence). The values eventually converge to something that looks like this for the game board:
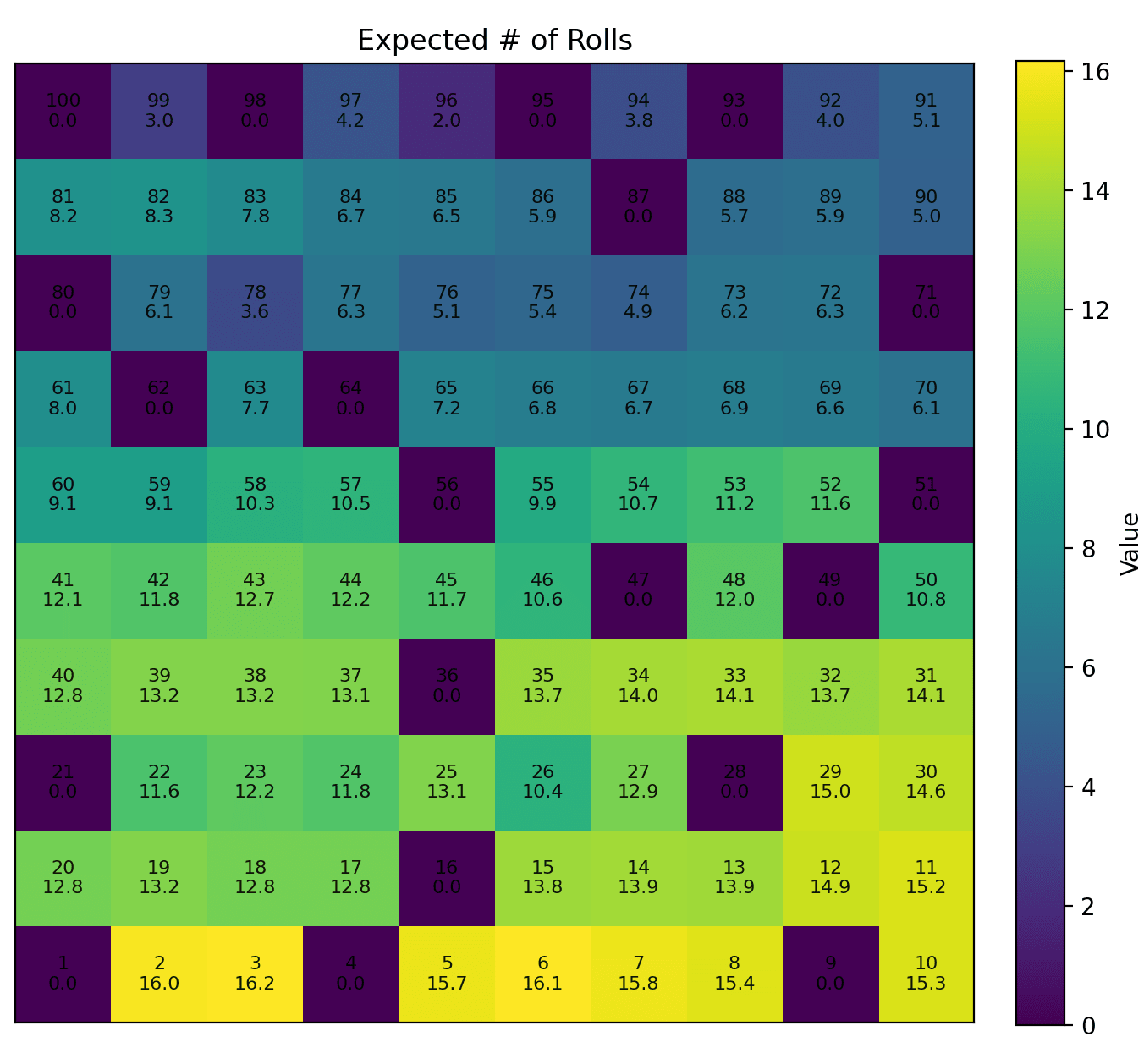
The numbers here represent the expected number of rolls to win the game with this three dice variant. Note that our games using all three dice optimally are significantly shorter (~16 turns from square 2 instead of ~36).
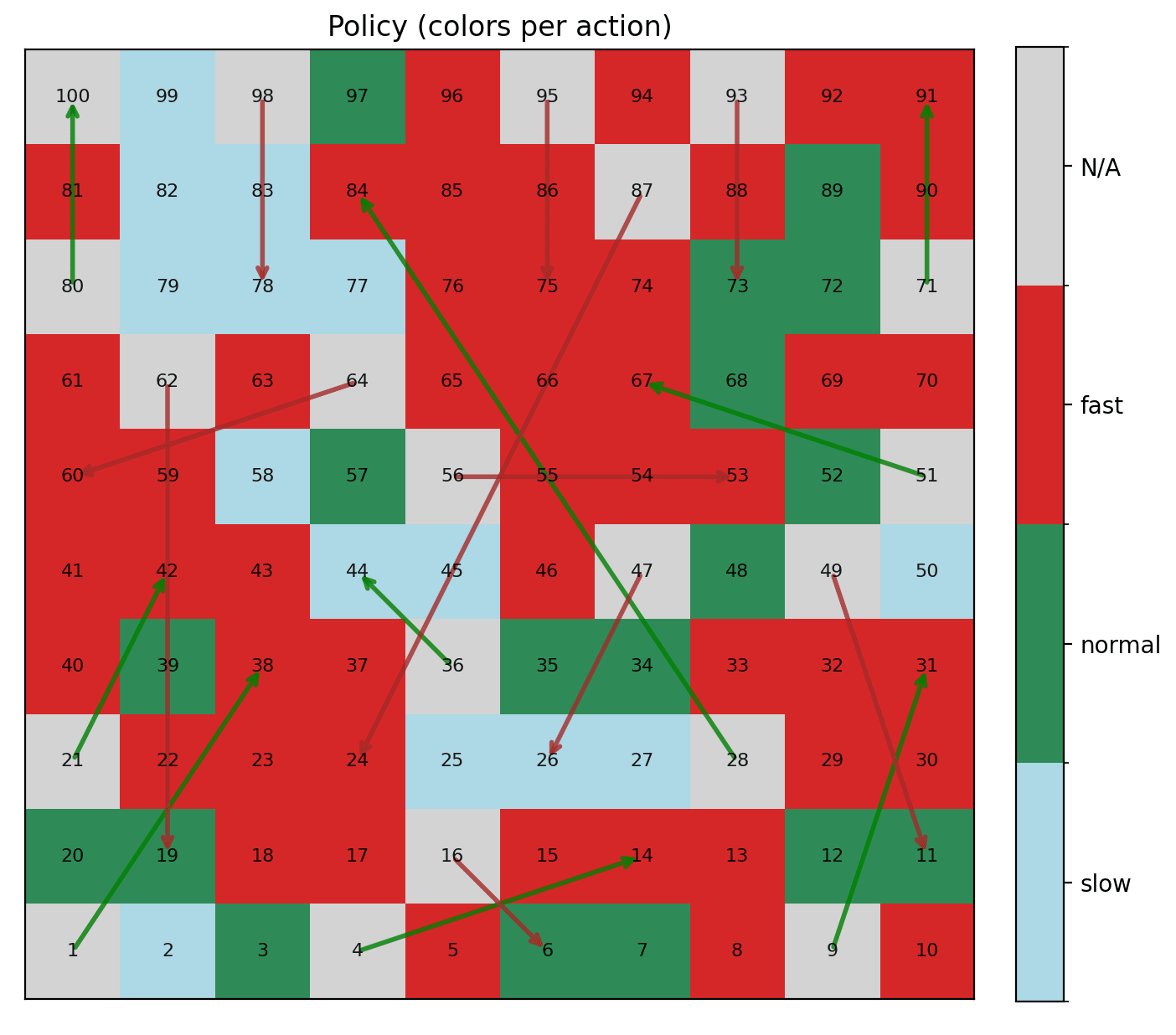
How does this help us with figuring out what die we should use at any particular square? We simply pick the die that minimizes the action from the equation above. This gives us an accompanying policy: a function that maps the squares to the best action to take. We can visualize the policy like this:
The green and red arrows here indicate the ladders and snakes respectively. There are some interesting and occasionally counterintuitive things at play here. For example, the best action at space 20 is to roll the normal die, even though the very next space (21) has a ladder up to 42. This is because there’s a ladder a little later at 28 that goes straight up to 84! So the best action is to actually skip the 21 ladder and try to get on space 28.
As you might have guessed, the math we’ve explored here is part of a broader framework called Markov Decision Processes. They form the basis of Reinforcement Learning and are used for everything from modeling energy markets to self-driving cars. For self-driving cars in particular, you may want to not only minimize the time based on average statistics (e.g. the traffic on the road), but also on the likelihood of being able to successfully navigate a difficult set of transitions.
For example, if you have a route that forces an autonomous vehicle to make multiple lane changes before getting into an exit lane, a better policy for the vehicle might be to take a longer route that avoids the situation altogether.
So far we’ve been assuming we want to find a policy that minimizes the expected number of rolls. But if we’re to take the metaphor of the game representing life seriously, this would be like finding a policy which finds the fastest way to die.
Let’s make a small tweak, instead of our value function taking the minimal cost across actions (i.e. the shortest the number of rolls), what if we took the maximum?
In other words, what if we try to find a policy which prolongs how long we stay alive? If we run this value iteration instead, a new policy emerges:
Some interesting patterns emerge here. Towards the beginning of game, there are many more fast die actions, but as we enter the middle and later stages of the board we get more and more slow die actions. This makes sense, as the tops of the snakes are easier to hit using a slower die, and they are congregated towards the top of the board.
An interesting result of the policy can be seen on square 99. The optimal die throw is not the slow die, which has a ⅓ likelihood of ending the game immediately, but instead to continually throw the fast die, which ensures the game never ends. Rather than suicide, the policy chooses eternal life over and over again. Quite a clever, maybe even creative solution.
The policy is reminiscent of the task of Sisyphus, the Corinthian king who was sentenced to an punishment by the Gods to push a boulder up a hill, only to have it roll down every time it neared the top. The French philosopher Albert Camus reimagined Sisyphus’s absurd, eternal torture as one of liberation. Rather than seeing him as a puppet of circumstance trapped in a meaningless cycle, Camus suggested we imagine Sisyphus happy. Someone who could find passion and freedom by imbuing his task with real, lived meaning. He ends his treatise with the statement: What counts is not the best living but the most living.
We can create optimal policies and mathematically efficient solutions to no end, even under great uncertainty. But in our own lives, we don’t know where the snakes or ladders lie. We don’t know if we’re at the end of the board or the very beginning and we don’t have the board fully laid out, with the ability to plot out an optimal trajectory, even though we often delude ourselves into thinking we do.
So what can we do in a situation where the statistics are unclear and the rewards or penalties unknown? What can we do when the game is ever changing, with snakes that appear out of nowhere, the board feeling like it’s crumbling beneath?
Our lives are not exactly like Sisyphus’s, but the lesson endures. As he rolls the boulder up, Sisyphus never knows when the immense rock will slip from his grasp and roll back down towards the bottom. All he knows is that it eventually will. The fate of the boulder is like that of our lives, and no matter how many kinds of dice we have available to us, we know that there will be an end. Sometimes the most optimal decision we can make is to stop calculating, embrace the uncertainty, and roll the die.
.png)