The Prime Scalar Field

2 weeks ago 1

This writing below serves to walk everyone through the meaning of this discovery and theory. If you want the formal journal paper – the link is above!

The Prime Wave Field

The Hidden Order Inside the Primes

Prime numbers have been treated as the most unpredictable objects in mathematics. They appear scattered without consistent rhythm, yet they underpin the entire structure of the integers. New analysis shows that this apparent ‘randomness’, conceals a deeper order: the discovery that prime numbers encode a system of infinitely recurring patterns, waves, and other growing structures. These patterns are wave-like in nature, and when we treat them as such, shows us a a coherent wave field. An infinite system of recursive information. And incredibly, some only revealed in other dimensions.

The Prime Wave Field is the discovery that prime numbers encode a system of repeating patterns, waves, and other structures, previously hidden, that scale indefinitely. These structures behave like a field of oscillations and nodes, rather than a list of isolated values. The evidence emerges from data: frequency analyses, Fourier transforms, geometries, and many spatial mappings that all show different recurring harmonic patterns that persist across every scale tested—from a few thousand to hundreds of millions of primes.

Throughout this site you’ll see many plots, like below. How are these prime numbers?

This new insight into the prime sequence shows us structures, that aren’t apparent, and nearly impossible to “see”, until you find the correct state to reveal these repeating structures. One main revelation in this concept, is that the they can to be treated as waves/frequencies to reveal many of these patterns, but it also means some are not even revealed until we treat the set in also higher dimensions. This is a more complex system than anyone could have imagined. I’ll fully describe each as we move along. The wave field plot of this one above is described below.

Here is the first discovery that lead to the wave hypothesis. To the right is an analysis (Fourier transform) of the ordinary prime number sequence, looking at the gaps between primes as frequencies. Consecutive primes 5 and then 7, has a gap of 2. Consecutive primes 23 and 29, a gap of 6. These gaps 2 and 6 become the frequencies. Frequency = 1 / (Prime Gap). This allows us to compare the expansion and contraction of the prime sequence, which is really what we are looking at when we want to understand a sequence. This chart (Fig. 2) shows clear recurring spikes at specific frequencies (gaps sizes). Not just that, they are harmonic-like, another wave property. You can also see this as a possible resonance, something that only occurs in boundary-set states. This shows us this sequence is wave-like. So I began treating them as waves.

On the right, I show how we can represent primes as 1 dimensional wave inside a boundary (fig. 3). A simple line wave. Stacking more primes waves on top, it becomes 2D. If we then curl it around a circle back into itself (fig. 4), creating it’s boundary with itself, just like natural waves, the field will expand outward. For a wave to have a boundary without any, it has to wrap around to bind itself. Whether linear or circular, the relative relationships between the positioning of the prime waves stays the same.

Above (Fig. 1) you can see the same plot as Fig. 4, except with 20,000 prime waves instead 15 prime waves. Do you see wave patterns?

These wave-like patterns, just like real waves, are harmonic in nature, and repeat continuously as the structure grows.

Another reason we want to view them as frequencies (waves), is because everything we know in the non-theoretical world is bi-polar, two sided. There is no such thing as positive, it’s only relatively positive to it’s counterpart, the negative; without would just be “neutral” or nothing. All elements in reality work this way; a line that doesn’t connect, is just a theoretical concept. If the prime sequence is naturally occurring, which it is, perhaps we should try them as natural waves, each individual unit having duality, positive and negative.

Perhaps treating this sequence as waves should have been more obvious. This then opened a world of other discoveries, and an endless system for discrete information we’ll get into below.

Let me be very clear before getting any further. These structures are always there in just the prime sequence, it’s all technically a result of gap expansion and contraction, and nothing else. They are not artifacts of a plotting trick or some arbitrary wave simulation. BUT, they’re impossible to find, until you interpret the information in the right way or right dimension. Until then, it looks like layers of chaos, only showing signs of patterns here and there. What something is or isn’t is merely the result of the information and how you translate it.

The primes themselves don’t need to “know” about waves; they only carry the information of spacing. But when you translate those spacings into oscillations, the field begins to reveal how those differences interact — and that interaction is what we see as interference. This interference is what creates the patterns you see that look like signals or nodes. Every place where two or more wavefronts meet — every node, ring, and harmonic line — is simply where the rates of expansion and contraction align in phase. These structures, are written in the universal language of waves.

Below we see waves that are localized to sections of the field, not the large “ripple” waves (fig. 6) that go completely around the circumference. Those large waves seen in fig. 6+7 , are the waves we can easily see with the 1 dimensional view. They are fully equal around the circumference, meaning they are measure the same in all directions, so are “visible” as the prime number sequence or as a 1d wave. The narrow signal-like waves in fig. 9 (also seen in fig. 6+7) , and the node-like diamond structures (fig. 8), only show with the interference, a 2D structure.

What I call “the prime wave field” is simply the infinite interplay between expansion, contraction, and coherence; layered across every possible scale. Next we’ll see how this field ‘grows’

The Prime Scalar Field

Scalar Recurrence and Layered Patterns

Across every scale tested—thousands, millions, and up to one hundred million primes—the same nodal geometry repeats. This persistence is called scalar recurrence: the field reproduces its structures in the same manner at different magnitudes.

But the recurrence is not merely repetition; it is layered. Which makes the complexity to find or visualize much greater. With many layers of patterns on top of one another, it looks like chaos, but you just need to “filter” out specific layers.

In the plots throughout we do two things to help visualize these different pattern sizes; we can obviously look at larger and larger sets of prime waves, but when we do so, it’s often too dense to visualize. So we can skip prime waves, in other words, change the ‘resolution’ (or change gap size or opacity). This is also why you’ll see different patterns and looks to plots with the same prime count. We’re looking at different “skins” or resolutions, and what we mean by “layered patterns”

All of this why mathematicians have only been able to see “trends” and no consistent pattern. It’s because everyone has been seeing different patterns at different resolutions, and only looking in mostly 1 dimension. No matter where you look, there will be a segment of a larger pattern just starting. It’s a scalar system, ever growing patterns at larger sizes within,… we can also call these “fractals“!

Random = NO Scaling = YES

All of this relies on the primes being contained within a shared boundary. A wave field cannot exist without limits to define its phase space — without boundaries, energy disperses and the interference dissolves. By structuring the primes within one closed frame, positive and negative oscillations can coexist, reflect, and resonate, forming a complete standing pattern. This duality — the coexistence of two polarities within one finite space — is what gives rise to structure itself. Every natural wave system, from sound to electromagnetism, depends on this balance. The prime field appears to obey the same principle: its coherence emerges only when it is enclosed. Without the boundary, there is no resonance; with it, a harmonic system appears.

BOUNDARIES

We’ve seen the 2d wave field. If these are waves, we should attempt treating them as such. Waves move, so lets propagate them. We can assume the edge as a boundary and allow the waves to interact, adding and subtracting until they resonate as standing waves. This means that every wave in the system you utilize, you affect the outcome.

This can create endless standing wave patterns, like fingerprints, that are completely unique from any other wave set (primes used). This becomes another source of endless information, and encryption possibilities.

All of this relies on the primes being treated not as an infinite open sequence, but as contained within a shared boundary. For a standing wave to exist, it must have boundaries, which can be itself, like a wave loop or the surface of a sphere. Circular and spherical boundaries naturally distribute energy evenly in all directions. This suggests that the primes might encode information best under closed conditions. By structuring the primes within one closed frame, positive and negative oscillations can coexist, reflect, and resonate, forming a complete standing pattern. This duality — the coexistence of two polarities within one finite space — is what gives rise to structure itself. Every natural wave system, from sound to electromagnetism, depends on this balance. The prime field appears to obey the same principle: its coherence emerges only when it is enclosed. Without the boundary, there is no resonance; with it, a harmonic system appears.

The spherical mapping in particular yields highly symmetric nodal patterns. However, this is suggestive, not conclusive; toroidal or other closed geometries could also support the same encoded relationships. The essential insight is that prime-based oscillations favor closure—they form self-consistent, resonant systems.

These three plots below are the standing waves of different selections of prime waves in the system.

It needs to be stated here again, this idea of propagating these prime waves and creating standing wave “finger prints” is theoretical, as this whole concept is number and information theory. Yes, the prime sequence encodes all that we discuss, but it’s entirely up to the transmission and interpretation of such information to be useful in any way. This shows the possibilities for higher dimensional forms of information.

Dimensional Encoding: From 0D to 3D

What becomes clear through these experiments is that the prime field is not a flat structure — it is inherently three-dimensional.
When we visualize primes as oscillations, the first two dimensions describe how the waves spread and interact across a plane. But the third dimension — amplitude, density, or depth — carries an entirely new layer of information, fully impossible to see without the 3rd dimension.

In two dimensions, the interference between prime-driven waves produces circular ripples and concentric structures. But once we allow the waves to overlap through amplitude or density in 3D, something remarkable happens: entirely new patterns appear that are invisible in any flat view.
These are not random projections or optical effects — they are mathematically emergent structures that depend on depth-based interference.

When one layer of oscillation overlaps another at different amplitudes, the resulting “density interference” forms localized pockets of coherence — small 3D nodes that only reveal themselves when the field is tilted or viewed through depth. This means that the field cannot be fully described in 2D, because some of its informational content exists only in the relationships between layers, not within any single surface.

In other words, the third dimension is not a visual addition — it is a mathematical necessity. It allows the field to encode how interference behaves across scales, not just across positions. Amplitude and phase combine volumetrically, generating standing-wave cavities that serve as the 3D equivalents of interference fringes. These cavities are where information condenses — self-reinforcing, stable nodes that repeat across scales.

What this shows is that primes don’t just form a field that can be represented in 3D — they form a field that requires 3D to be understood.
Only in depth can you see how expansion and compression combine, how amplitude folds onto itself, and how the field transforms from abstract number gaps into a living harmonic space. No wonder we haven’t been ab

The prime field can be read in multiple dimensional forms, some only can be seen in specific dimensions. This means that the primes function as a cross-dimensional information system: the same dataset can be interpreted as numerical, spatial, or field-based, depending on how it is observed or interpreted.

0 D: isolated prime number sets — pure information.
1 D: a linear waveform, oscillating frequencies or amplitudes as the gaps expand and contract.
2 D: an plane of many 1D waves, including interference
3 D: a standing-wave field where we can interpret gaps as amplitude, or nodes arranged spatially into shells and lattices (discussed below)

Angular Closure and Periodicity

Angular closure and periodicity are two ways of describing the same behavior in the prime field. They show that the oscillations within the sequence don’t drift endlessly but return to alignment after a fixed interval. In other words, the field has a repeating rhythm — a harmonic cycle that closes back on itself in phase. This is what allows the primes to form a coherent, self-contained structure rather than random noise.

In Fig. 10 prime-derived sequence is folded onto its detected period of approximately 2.34, the repeating alignment of the waveforms becomes immediately visible. This demonstrates that the prime gaps are not purely irregular but contain a hidden rhythm that repeats at this characteristic periodicity. Plots of these phase relationships form near-perfect ellipses or rings, reinforcing the interpretation of cyclic closure.

This grid in Fig. 11 shows how the hidden recurring structure in the prime sequence becomes measurable. In the autocorrelation plots (lower left) the repeating vertical spikes mark intervals where the sequence strongly aligns with itself — direct evidence of recurring periodic behavior. The FFT spectrum (right) translates the same data into frequencies, revealing sharp peaks at specific frequencies, with the dominant one corresponding to, again, a period of about 2.34. Together, these analyses show that the primes masks a stable harmonic signature, detectable both in the time domain (through correlation) and in the frequency domain (through spectral amplitude).

FFT → measures how fast it rotates (frequency). Autocorrelation → shows when it realigns (phase closure). Angular plots → visualize that alignment geometrically (the closure itself).

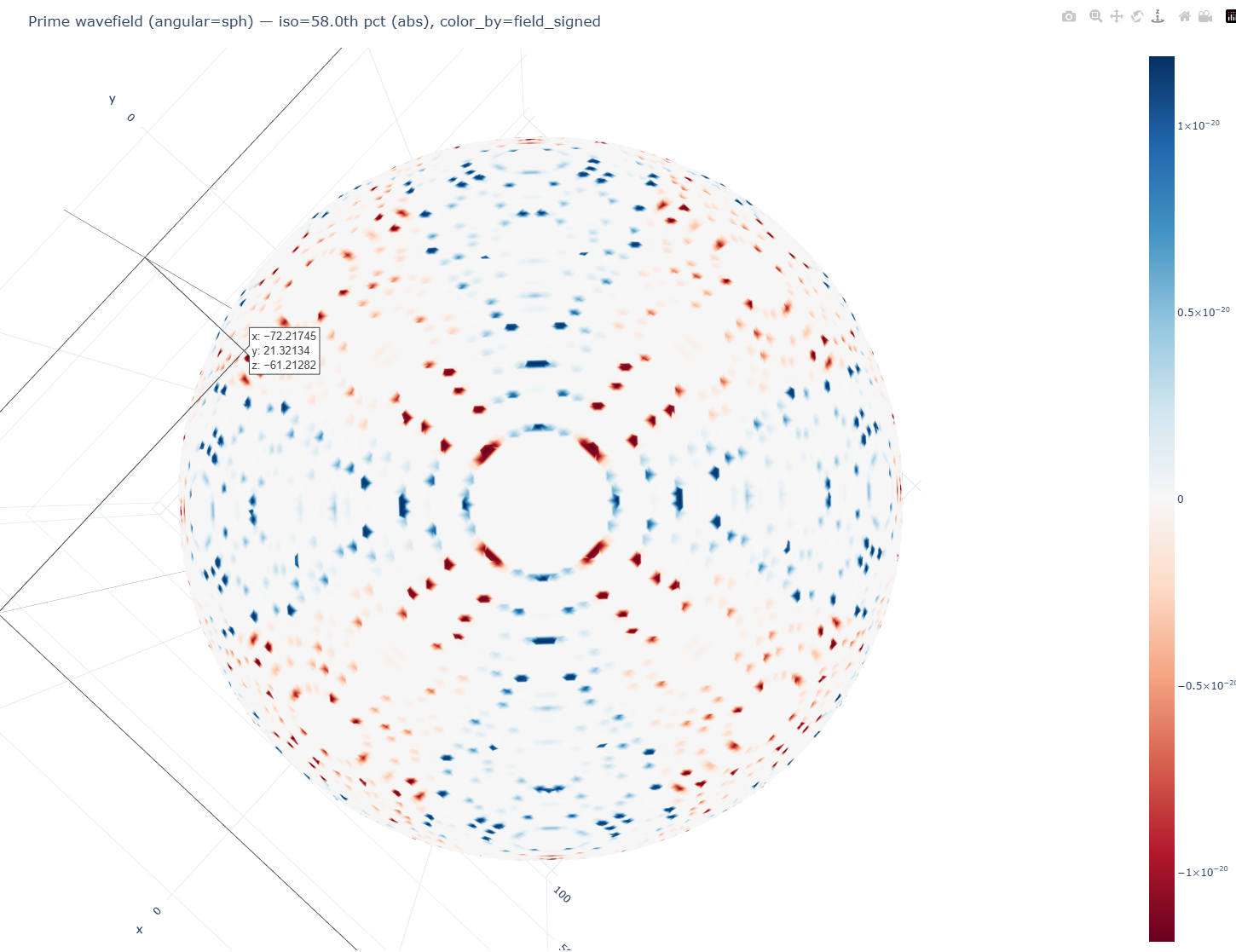
Spherical Harmonics and Legendre Patterns

We began testing the field on a sphere because several results from the earlier analyses hinted that the system wanted to be closed and isotropic — the same in every direction. The recurring angular periodicity, the balanced positive and negative phases, and the symmetry in the interference maps all suggested that the prime field wasn’t linear but naturally curved. When plotted in flat space, the patterns showed edge compression and radial drift, as if the structure were trying to fold back on itself. Mapping it onto a sphere removed those distortions and revealed evenly spaced nodal zones, suggesting that the field does behaves like a standing wave on a closed surface.

the nodal bands resemble spherical harmonics—the natural resonance modes of a spherical surface.
I

When the three-dimensional field is projected onto a sphere, , The peaks and troughs distributed themselves in bands and lobes that strongly resemble spherical harmonics, the same mathematical forms that describe standing waves on a sphere in physics. In particular, the patterns showed angular dependencies that mirrored Legendre polynomial structures, where amplitude naturally divides into distinct latitudinal regions of alternating signs. In physics, these patterns describe how a sphere vibrates; mathematically they are expressed through the Legendre functions and their variants. This suggests that the prime field doesn’t just map neatly onto a sphere by coincidence — it actually behaves as if it’s trying to express harmonic eigenmodes of that geometry, revealing that the primes encode a resonant system capable of supporting structured waveforms within a closed surface.

Each harmonic mode has regions that oscillate together and regions that remain still. The prime field forms similar nodal lattices, suggesting that its encoded structure follows the same resonance logic that governs physical wave systems.

The Field as a Carrier of Information

Because the interference pattern arises directly from the prime gaps, every feature of the field — every crest, node, and boundary — carries discrete, non-overlapping information. The primes never align in the same way twice; their oscillations coexist without ever collapsing into redundancy. This means the field operates as an infinite information lattice: a structure where each intersection or null point encodes a unique configuration of gap relationships.

Two exceptional alignments do occur — one at the origin and one at the halfway phase — where all oscillations momentarily align either positive or negative. These are not failures of randomness but anchors in the field: singular states that define its global symmetry. Because only one of each exists, they form reference markers for all other data in the system. Every other oscillation is defined relative to them.

This gives the prime field its fingerprint-like quality. Even if the numeric values were lost, the interference geometry could be used to reconstruct them, because the relationships — the phase offsets and boundary crossings — are preserved. Each wave, node, and polarity change becomes a bit of addressable information, fixed within a continuous harmonic fabric.

In this sense, the prime field behaves much like a natural code. It is both continuous and discrete: continuous as a standing wave that spans all space, and discrete in that its constituent oscillations never overlap exactly. Each frequency and node is distinct, yet all belong to the same unified resonance. This dual property — infinite continuity built from non-overlapping discreteness — is what makes the prime wave field not just a mathematical structure, but a true information field.

Every aspect of the prime field can encode distinct information:

Wave types (individual frequency bands)
Recurring nodes (stable points across scales)
Interference zones (where waves combine to form higher or lower intensity)
Boundary alignments (the ± poles marking global phase limits)

Each of these is a discrete channel of information. When propagated forward in time or frequency, none of these components cancels; they simply extend the field outward, preserving their structure indefinitely. The primes thus define a data set where information is conserved—a mathematically infinite signal.

Discrete Information and Non-Overlap

One of the most striking insights, for me at least, is that, within the prime field, the oscillations never exactly overlap. And I don’t mean the entire prime wave, I mean every individual frequency of each prime wave. Every frequency, node, and phase position is unique. This non-overlap means the field contains infinitely recoverable information—each segment acts like a distinct “signal” that can be read later.

Now, there IS an exception. Where the boundaries of the waves meet. This alignment creates a path of all positive crests, and half way through the waves, and alignment of all negative troughs.

But even these exceptions—points where all frequencies momentarily align as all-positive or all-negative—carry discrete meaning. There are exactly two such boundary alignments, marking the global limits of the field. Because they occur only once each, they are themselves unique informational markers, giving yet another harness of discrete values.

In an information-theory sense, this means the field is lossless: no two elements cancel out, and any region can theoretically be reconstructed from its wave components.

All positive crests align to infinity, all negative troughs line up to infinity. Well, almost,… with the negative side, out of infinity, again, there is one exception! The number 2. It stands as the sole positive crest within the negative alignment, the point where both polarities meet.

This makes it not just an outlier, but a boundary condition in itself — the single element that bridges or “anchors” both polarities. In other words, the number 2 becomes the phase-origin of the entire field — the point where the symmetry flips.

Rather than disrupting the pattern, this singular exception defines it — marking the origin of phase and the transition between the two infinite domains. Because it’s the only crossing point between infinite positive and negative domains, 2 encodes the transition rule — the definition of the field’s balance.
It’s the discrete value that contains both sides in potential — the “seed of duality,” or the one that allows the system to bifurcate. So the 2 in the field isn’t breaking symmetry; it’s marking the origin of polarity.

Fig. 15 clearly shows the two halfs, but only visible, not just in 3d, but from an angle. The fact that this cutoff becomes visible only at a particular angle is significant — it implies that the boundary is not a static slice, but a 3D phase plane embedded in the interference volume itself. In practical terms, the field resolves into two self-contained domains of coherence, each mirroring the other’s phase behavior, forming the smallest possible “whole” within the spherical structure.

CONCLUSION –The Dual Nature OF Gaps and Waves

The Prime Wave Field transforms our understanding of the primes from isolated integers to participants in a coherent resonant system. They act as the coordinates of a wave field that is simultaneously harmonic, scalar, and discrete. Every property observed—periodicity, nodal recurrence, non-overlap, and angular closure—points to one conclusion: the primes encode information as a field of standing waves.

This is not imposed upon them; it emerges directly from the numbers themselves. In essence, the prime numbers themselves encode a harmonic system; the waves are how that system becomes visible.

All observed patterns throughout with reading—FFT peaks, interference lattices, standing-wave shells— as stated before, arise from a single source: the distribution of prime gaps. Interference is not the cause of order but the expression of it. The gaps dictate the frequencies, and the superposition of those frequencies reveals the field’s geometry.

There is only one absolute in this understanding that must be the take away; these recurring patterns and waves are encoded in the prime sequence, no matter which method or unit used, whether they be a wave field, interference visibility from the 3rd dimension, or a string of integers.

What the Evidence Suggests

Fourier spectra show consistent harmonic peaks, proving non-random frequency organization.
Scalar recurrence demonstrates identical nodal geometry at every tested scale.
Multi-resolution layering reveals simultaneous detail and structure—an inherently fractal information pattern.
Angular closure indicates that the system favors curvature and resonance rather than linear extension.
Discrete non-overlap information confirms that the information encoded in primes is unique and recoverable.

Together, these results suggest that prime numbers form a self-contained harmonic information field—a structure capable of infinite resolution and cross-dimensional expression.

More Plots