A/N: This post is an amalgamation of several different things I wrote for/discussed with various people that happened to overlap a lot, so if the arguments seems kind of run-on, that’s probably why. Also, if a particular argument seems a bit too technical, just skip over it. The arguments are not that tightly linked, and I would like to believe I have a lot of different interesting stuff to say.
What exactly it means to learn something? I ask this question to discuss the idea that ChatGPT should not be used for learning because it sometimes hallucinates, and therefore it’s possible to learn wrong things from it.
This idea bothers me because ChatGPT has been extremely helpful for me in learning things. Like, I like watching Physics/Maths/Engineering/etc. videos, but there’s is always some pre-requisite knowledge that I either do not have or have returned to sender. This makes it difficult for me to learn from those videos, because 1) I am by default skeptical of anything I don’t fully understand, and 2) it’s always easier to remember a coherent set of facts than a disparate set of facts (e.g. if A and B imply C, then even if you forget C, you can derive it again easily).
In theory, I could just “refer to a textbook” to fill in the gaps in my knowledge, but for as long as I have wanted to be a polymath (ever since I read a Horrible Histories book about Leonardo Da Vinci in primary school!), I have never ever once done that because 1) searching for a particular fact in a particular textbook is PITA, and 2) there’s no guarantee I will find what I want in any particular textbook! Whereas ChatGPT just evaporates this friction/search cost.
But how do I reconcile this usefulness with the possibility that the search results might be wrong? It clicked into place for me when I read this absolutely profound, mind-shattering quote by the chemist Antoine Lavoisier:
“…strictly speaking, we are not obliged to suppose [caloric] to be a real substance; it being sufficient … that it be considered as the repulsive cause, whatever that may be, which separates the particles of matter from each other; so that we are still at liberty to investigate its effects in an abstract and mathematical manner.”
“Caloric” being the hypothesised “small particles of heat” that get in between the the larger particles of matter, thereby explaining why things expand as they get hot. We now know that’s NOT what heat is, but that’s not the crazy part! The crazy part was Lavoisier was fully aware that he might have been wrong, yet it didn’t matter, and he knew that it didn’t matter! And it didn’t matter because all he needed was something that explained what he already knew, and that he could empirically test.
(I would strongly recommend reading at least the first post of the linked series. It has that wonderful and frustrating quality of writing down every idea I thought I was brilliant for figuring out, except done much better and three months before I even thought of the ideas.)
In other words: If as far as I can tell what ChatGPT is telling me is correct, then it is effectively correct. Whether it is ultimately correct, is something I am by definition in no position to pass judgements on. It may prove to be incorrect later, by contradicting some new fact I learn (or by contradicting itself), but these corrections are just part of learning.
Does this seem unnecessary? Surely, if there already exists a correct answer in a textbook somewhere, its absurd to learn the wrong thing first then learn the correction? But this assumes the correct answer can be easily found! Is it also absurd for an English mathematician to re-derive proofs an Indian mathematician presumably already discovered centuries ago, rather than embark on a months-long quest to India to find some ancient book of proofs?
There’s a trap that I’ve fallen into and I think most people who are half serious about learning things fall into, which is that its very hard to determine whether something is true. So if our heuristic is that we should learn something ONLY if we can be absolutely sure that it is true, what we will learn is absolutely nothing. Even worse, because we only become confident that a new fact is true when we 1) know a lot of facts, and 2) that new fact doesn’t contradict any other fact we know, we become stuck in an shitty equilibrium where we don’t know anything and therefore don’t dare to learn anything!
(By the way, I cannot express how utterly inane I find the “gotcha” argument that if you don’t know a topic well it’s impossible to determine when ChatGPT is hallucinating, but if you already know a topic well you don’t need ChatGPT. But it’s obviously much easier to check that an answer is correct than to come up with a correct answer, to check that a sudoku is correct than to solve the sudoku, and to tell that a restaurant’s soup is disgusting than to make non-disgusting soup. If you had a box that spat out Nobel prize-winning tier ideas 10% of the time you pressed a button and all you had to do was check what it spat out, you have as many Nobel prizes as your heart desires.
I’m not saying there’s no reason to insist on rules like “listen to the experts, only learn what is true”, but the reason is NOT that it’s more efficient at an individual level. It’s the same reason journals insist on a 5% significance threshold even though its arbitrary and doesn’t really do a good job separating good from bad research. It’s a rule that may be more efficient at the aggregate level, not because it’s impossible to do much better, but because it’s possible to do much worse.
But as an individual that’s entirely irrelevant to me, because I am not the entire scientific community! Who cares if I’m slightly wrong in the short term? Absolutely nobody!
There is a more fundamental point I want to make, which is that I don’t think knowledge is static.
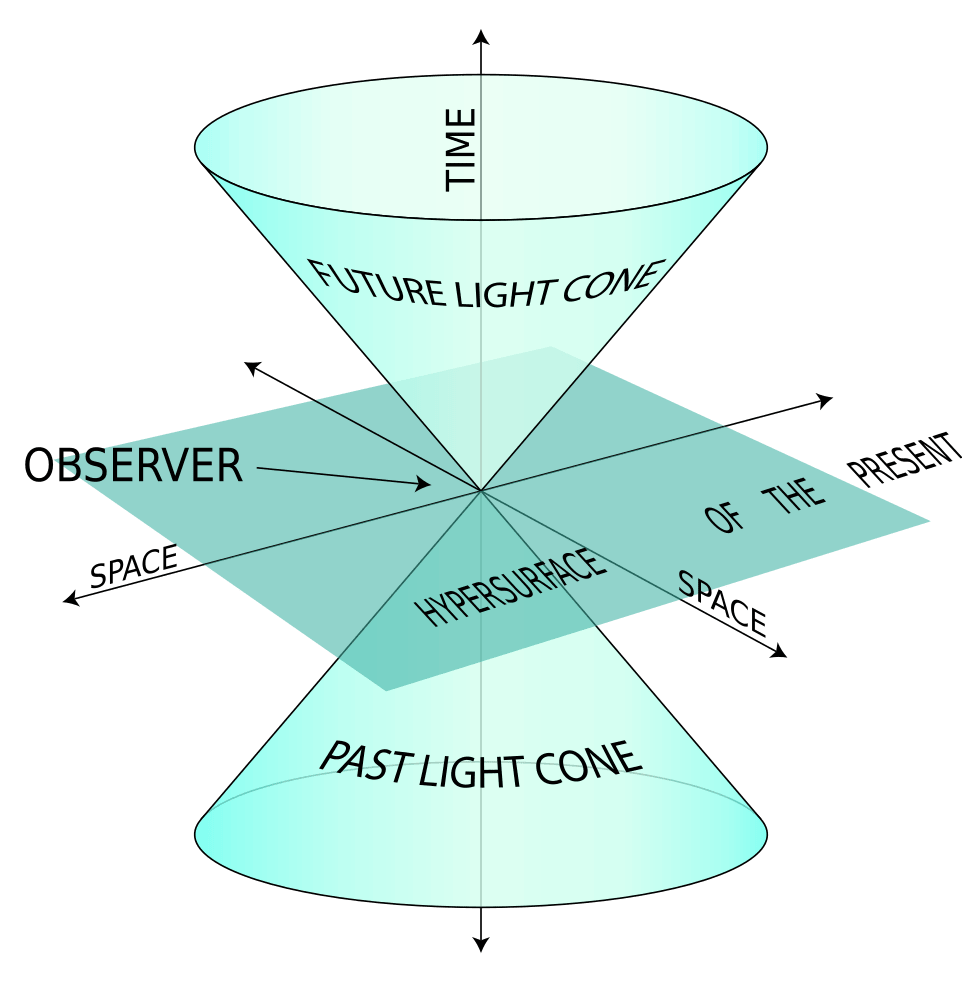
Knowledge is not static because there is no singular “truth”, and there is no singular truth because 1) things are always changing, and 2) information requires time to propagate. Consider this: If I send true information from point A at time t=0, and you receive the information at point B at time t=1 that no longer matches what is happening at point A at time t=1, is the information you receive true or not true?
There is a feeling of paradox, because two definitions of truth have been conflated. The first being that information is true if it corresponds to the process that produced it (which our information packet satisfies), and the second being that information is true if it is always and everywhere true (which our information packet fails to satisfy).
Both definitions are worth discussing. The first definition (the correspondence definition) is extremely powerful. It’s why learning works at all. Just by using mental models that correspond to observations, we’re able to “see” space-time bending in our minds, long before we can actually empierically observe it. But this power comes at the cost of complexity: We now need to keep track of multiple possible states of things rather than just one.
The second definition (the always and everywhere definition), while in some cases is inexplicably always literally true (e.g. Newton’s Law, Maxwell’s equations), is in many cases more of heuristic that controls complexity. Granted, it’s a very powerful heuristic, because for some reason our universe is full of systems that converge to stable states, or at least don’t diverge outside of some bounds.
(I could also make an anthropic argument that if something continuously diverges relative to a reference process, then it eventually becomes unobservable. Therefore, whatever we can observe must necessarily be the result of a non-divergent process. There’s a great Futurama clip that captures this idea, about an evil AI Amazon that expands to envelop the Earth, and then the Sun, and the whole Universe, at which point everything becomes exactly as it was before.)
All of our measurements rely on some reference object that is more stable than the things we want to measure. And most of the time, when we say something is true, what we really mean is that it is stable. That’s why mirages and speculative investments feel false, but the idea of the United States of America feels real, even though there’s nothing we can physically point to that we can call “the United States of America”.
For something that I kept seeing everywhere (the familiar “...converges in distribution to a normal distribution...” in Statistics, the whole idea of equilibriums in Physics), it somehow never occured to me until quite recently how fundamental the idea of convergence was. Without convergence it would be practically impossible to know anything!
Like, what even is probability? We assume that the current state we are observing deterministically followed from some previous state according to some set of rules. We don’t know what the rules are, exactly, so we make a model that approximates the observed outcomes.
But what exactly is an “outcome”? Suppose I throw a die in a spaceship, in a submarine, in a dive bar etc. and they all land on the side the shows six black dots facing up but rotated at different angles and lying on different surfaces. Are these three outcomes or just one? If you claim that these differences don’t matter, and that they’re all just the same outcome, what justifies the claim?
We define all specific instances of “landing on 6” as equivalent, even though there are many different things about each die roll, because when we place a bet on the outcome of a die, we only bet on the number of dots facing up. So our mental model of the die compresses its entire end state space, throwing away information about an infinite number of “micro-states” to just six possible “macro-states” of a die.
But it also does something else: If I go back one microsecond before the die lands flat, a larger infinite number of “micro-states” of dice in the air converge onto a smaller infinite number of micro-states of dice on flat surfaces. What if the universe worked differently, and every time we threw a die it multiplied into an arbitrary number of new dice? How would we even define probability? Which is to say, a probabilistic model fundamentally compresses information by mapping many microstates to single macrostates, but this compression is only ontologically valid because we are modelling a convergent (or at least non-divergent) process.
It always confused me why the Central Limit Theorem worked. Like I can follow the math, whatever. But WHY should the sample means of arbitrary distributions all converge towards normal distributions?!?! Until I realised my bad habit of not reading definitions carefully had doomed me once again, once again, and had I properly read the statement of the theorem, I would have realised that the CLT only works for distributions with finite mean and variance! In other words, it models a convergent (or at least non-divergent) process!
No fucking shit the sample mean of a convergent process converges!
The implications of the convergence requirement are more serious than just making the CLT feel more intuitive. Anytime we rely on any statistical method that uses the CLT we rely on an assumption that the process we’re modelling is convergent (or at least... you get the point, I don’t want to repeat “non-divergent” over and over). It’s one thing to say “averages are misleading, you could drown in a river that’s on average a metre deep, teehee”. It’s another to say, actually, there isn’t even a meaningful average for any sub-group, because the process is actively diverging! (Undergraduate level) Statistics is completely meaningless in that context! And here I’m thinking very specifically about statistical claims about intelligence, but I’ll get into that later, so let’s move on.
A question we could ask is why physical systems seem to converge so often (other than the unsatisfactory anthropic argument). To answer this question, I’m going to do that irritating thing where I define something that’s poorly defined, in terms of another thing that’s poorly defined. I think a huge part of why systems converge is because of diminishing returns. Diminishing returns is one of the things you learn about in a specific context, like, “20% of the work gets 80% of the results because of diminishing returns, so you shouldn’t waste time and effort trying to get things perfect.” And you don’t really think about it much outside of that context.
But it’s so much more than that.
When I first read about how poorer families tended to be more generous with helping their family/neighbours, so that when they needed help they would be able to get it, I was very confused. If you’re in that situation, why not just skip helping others that one time, and save enough so that you wouldn’t need help in the future either? Why go to all that hassle just to shuffle the same savings around? It was only later that I realised, oh, it’s because costs are not linear. If you need salt now you could walk over to my house and borrow it instead of going all the way to the store (at least until your regular grocery day, at which time the marginal time cost of buying salt is zero), and vice versa. And pretty much every form of social cooperation is a way to unkink non-linear utility or cost functions. Division of labour? Those ten thousand nails I can make in a month by specialising in nail-making aren’t going to do me any good if I’m only making them for myself. Alone, the non-linear increase in my efficiency at producing nails as I spend more time producing them is more than matched the non-linear decrease in my utility (I would starve to death.)
So how exactly does diminishing returns lead to convergence? We could observe that diminishing returns goes up sharply and then has a flat bit at the end, and convergence similarly goes up sharply and has a flat bit at the end, and surely those two observations must be related. But we can do a bit better than that.
Suppose Alice and Bob are both making dongles at a dongle factory, and Alice is a lot better than Bob at making dongles. But suppose you needed keychains to make dongles and both Alice or Bob can make many more dongles than there are keychains to make them with. In the end, both Alice and Bob will make exactly the same number of dongles, Alice will just get there slightly faster than Bob. And maybe it’s obvious that everyone stalls at the frontier of human knowledge. But is it equally obvious that even if Alice has a number of different actions she could do with different potential payoffs, that to a certain extent it doesn’t really matter which action is the most optimal?
If it’s kind of ambiguous whether option A or option B has bigger payoffs, and their payoffs are independent, it’s more optimal to just pick one at random than waste time and effort trying to resolve their actual payoffs. Whichever one you pick to start with, diminishing returns are going to set in, at which point you pick the other. You’ll always end up picking the same set of options over a long enough planning horizon.
A dynamic model of knowledge also solves a paradox for me: In Statistics (at least in the context of Psychology and Economics which are slightly more familiar to me), its a big no-no to look at the data, form a hypothesis from the data, then verify that yes indeed our hypothesis matches what we observed.
But this makes no sense to me because 1) it implies that to form a valid hypothesis, you need to have never observed any empirical data, and essentially make hypotheses at random, and 2) the process of observing things and coming up with rules that could have generated those observations is exactly how early scientists came up with rules like e.g. KE = 1/2 mv^2, and those rules seem to work perfectly fine!
I think the solution to this paradox is that Physics as a field of knowledge converges much faster than either Psychology or Economics. So in Physics we can safely assume anything at the scale we can observe is already stable, whereas in something like Economics we don’t have the same guarantee. Using different data is a soft check that we’re in a semi-stable, somewhat generalisable region of observations.
Knowledge is also dynamic in the sense of: What I know today different from what I know yesterday, in a way that’s more complex than just adding/learning or subtracting/forgetting facts.
A lot of ink has been spilled over students forgetting what they’ve learnt over holidays or how as adults most of us have forgotten most of what we learnt in school. Now, one argument I find plausible for why its still a net benefit to put everyone through school is that even if individuals forget, society as a whole remembers.
I remember plenty of times I told someone something, forgot it, and then they ended up telling it back to me. In this view, packets of knowledge circulate around like boats on a river, and even if some of them sink, the important thing is that some of them get to where they need to be.
But another view we can take is that of packets of knowledge filling up warehouses long before they are needed, like a huge shipment of car parts for a specific model of car, that not only takes up space that could be used for more immediately useful things, but also rusts into uselessness long before anyone even attempts to put them to use.
(I find the argument that going to universities for four years somehow shapes the minds of students in some vague, beneficial way to be pure nonsense. It reminds me of the moral panic back in the early 2000s, when video games started to become mainstream, that violent video games somehow “rewired children’s minds”, as if 1) minds are so easy to rewire, and 2) minds are thereafter impossible to rewire by, like, playing Harvest Moon or something.)
Knowledge decays. To some extent, this decay is good! The fuller our warehouse is, the harder it will be to find what we want in it. I think this idea and a lot of ideas in this essay are more obvious to me as a software engineer, because software engineering as a field thinks very explicitly about the organisation of knowledge. We cache the results of database reads we expect to use again soon, so we can make cheap cache reads instead of expensive database reads. We put CDNs between the server in the U.S. and the person loading videos in Asia so our horsegirl waifus don’t have to be delivered from halfway around the world.
Knowing that we can organise knowledge to make the use of it one billion times more effective is awesome power, but with awesome power comes the great PITA of actually having to organise said knowledge, because now we need to keep track of:
Is this knowledge directly, practically useful?
If it is not directly useful, can it be eventually useful in constructing something that is?
Out of all knowledge that satisfies either the first or second criteria, which should I learn now, based on (non-exhaustively):
Do I have enough pre-requisites that I can make progress?
Which is most immediately useful e.g. learning a new tool for my job vs studying Physics?
Which has the largest long-term payoff e.g. learning a new tool for a job vs Physics?
Which has the most support e.g. teachers, friends who are learning the same thing?
Which is most “coherent” with other things I’ve learnt recently, since it’s easier to learn/not forget a coherent set of facts? (Annoyingly, this trades off against interest saturation, where you get bored of doing the same thing for too long.)
Which is “small enough” that I can actually learn it in the free time that I have? (As opposed to getting extremely confused, running out time, then having to start over the next time I try again).
And the answers to all of these questions are changing dynamically, because learning one set of things makes learning a second things easier, and at the same time it means I’m actively forgetting a third set of things. Add to that, the free time I have is always changing, and what I consider immediately useful also changes every time I get pissed by a Physics lesson or 3Blue1Brown video that I just. don’t. get.
There is also something else that I think anyone who has spent a good amount of time trying to learn stuff intuitively gets, but I don’t think I’ve ever come across someone explaining it explicitly. There is something very natural about representing knowledge as a kind of directed graph, where some nodes are central, and others more tangential. So something like F = ma is more fundamental than, say, something like a = v^2/r for centripetal acceleration, even though both have the form a = something, because you derive the second under the constraint of uniform circular motion, while the first is always true.
And as fucking obvious as that sounds when stated like that, equations confused the shit out of me for the longest time. Like, obviously I was supposed to rearrange letters to get the solution, but then I tried to rearrange letters in a different (but still mathematically valid!) way from the teacher and I would get a contradiction?!?! And the problem is that maths is fucking bullshit no one ever tells you that the maths that is written down is missing a bunch of stuff you’re just supposed to keep track of in your head! What’s the difference between a function and a transform? Or a function and an equation? Absolutely nothing, except what you’re supposed to map the letters to in your head!
If we have a whole bunch of letters interspersed with operators and an equal sign, there’s a whole of bunch things we could be describing. We could be describing a universal constraint, like F = ma. We could be describing a universal update rule, like a = F/m or the curl of E = -dB/dt. We could be describing a conditional constraint or update rule, like V = IR for ONLY for resistors or a = v^2/r for uniform circular motion. We could be describing a guess, like y = βx + ε. Heck, we could just be defining a thing i.e. sticking a label on some useful repeating group of letters and operators.
Another problem I always had was that I would put the numbers in the letters BEFORE I rearranged them, which in hindsight is just, LOL. I like to think that I was just extremely literal as a child/teenager as opposed to just extremely dumb. So I friggin love this quote from Judea Pearl, which shows that no, I’m not extremely dumb, confusion caused by the lack of explicit directionality in equations is very common:
“Economists essentially never used path diagrams and continue not to use them to this day, relying instead on numerical equations and matrix algebra. A dire consequence of this is that, because algebraic equations are non-direction (that is, x = y is the same as y = x), economists had no notational means to distinguish causal from regression equations.“
Ouch, burn!
Having a sense of what is fundamental and in which direction we’re supposed to go matters! Because the way maths works is that if A and B imply C (and vice versa), you could just as well say B and C imply A, except NO! You can’t! Because by trying to derive the general from the specific, you’ve introduced an assumption that wasn’t supposed to be there and now somehow 0 is equal to 2!!!
Even if there’s no obvious contradiction, it’s OBVIOUSLY WRONG to be in the first week of class and derive Theorem B from Theorem A, and then in the second week of class derive Theorem A from Theorem B (or define work as the transfer of energy and energy as the ability to do work; or describe electricity in circuits using water in pipes and then describe water in pipes using electricity in circuits). NO! Nonononono!
“If we have discovered a fundamental law, which asserts that the force is equal to the mass times the acceleration, and then define the force to be the mass times the acceleration, we have found out nothing”!
The only description of knowledge that makes sense to me (for now), is that we start from observations, then somehow or another we derive rules and entities that would have produced those observations. Now, at this point, neither the empirical observations nor the theoretical rules are necessarily more privileged, since the observations could be mistaken or the proposed rules could be wrong. But there will be rules that seem more incidental, where changing them would only change one or two specific predictions, and rules that seem more fundamental, where changing them would require re-jiggering every other rule. If our beliefs and new claims contradict each other, one of them must be wrong, but which? The silliest thing in the world to do would be to either always reject our original beliefs or to always reject the new claims.
No, the only sensible thing to do is to reject the least fundamental claim. Even if the universe has conspired to mislead you through coincidence about what’s more fundamental, the rules which we perceive to be more fundamental are in any case the rules which encode more and a wider variety of observations, and so it’s perfectly sensible to require more contradictory evidence before we reject them.
There are, of course, also something like “in-between” rules that are very difficult to map onto any physical object except through convoluted chains of logic but which allow us to bridge between “clusters” or rules and the observations they encode.
Awareness of the existence of “bridging rules” solves what used to be a very big problem for me. Because like every overly-stubborn “clever” child, I was very, very insistent on trying to DERIVE EVERYTHING from FIRST PRINCIPLES, which works out about as well as you would expect. But once we have a map of rules and observations laid out as above, it becomes clear that 1) there is no privileged starting position to derive everything else from, we can reasonably start from any base of facts, and 2) some parts of the structure are much more inherently stable than others. Rather than trying to cross the swampy ground between domains by clinging onto a narrow rope of one-off proofs, it’s much more practicable to go directly from solid ground to solid ground and explore “nearby”. We would spend much less time and effort trying to avoid sinking into the ground/forgetting what we’ve learned, and in any case what we learn would be much more directly applicable to the observations we actually care about.
(As a side note, I’m aware that many people have tried to do something like making a graph of some domain of knowledge and using that to make automated inference which just... doesn’t work. I’m not entirely sure what accounts for the difference between what I’m describing and those attempts. But I would guess that I’m using the concept of a knowledge graph in a more general way to decide what I want to learn, as opposed to trying to derive specific conclusions; as well as having a more dynamic approach where I’m constantly emphasising/de-emphasising nodes as opposed to trying to pin down a “canonical” graph.)
“In complexity there is agency, if only you have the wit to recognise it and the agility and the political will to use it. [...] Southeast Asia is a naturally multi-polar region. It’s not just that the U.S. and China are there, but there is Japan, a U.S. ally but whose interests are not exactly the same. There is India, there is South Korea, there is Australia [...]. So there is a multi-polar environment, which increases maneuver space.”
Bilahari Kausikan, Managing U.S.-China Competition: The View from Singapore
“I think there’s an even more important reason to be skeptical of ‘polycrisis’: buffer mechanisms. The global economy and political system are full of mechanisms that push back against shocks. Supply-and-demand is a great example — when supply falls, elastic demand cushions the short-term impact on prices [...]. [B]uffer mechanisms often push back against problems in addition to the ones they were designed to push back against [...]. In other words, sometimes instead of a polycrisis we get a polysolution.”
Noah Smith, Against “Polycrisis”
“[I]magine a study where we ask the question, ‘are red cars faster than blue cars?’ You can definitely go out and get a set of red cars and a set of blue cars, race them under controlled conditions, and get an empirical answer to this question. But something about this seems very wrong — it isn’t the kind of thing we imagine when we think about science [...]. Science does have to be empirical. But being empirical is not enough to make something science.“
SlimeMoldTimeMold, The Mind in the Wheel – Prologue: Everybody Wants a Rock
I love complexity. And if you can in any way describe yourself as an underdog, you should love complexity too. Because, if it was obvious what the most obvious winning strategy or winning investment was, whoever starts out with the most authority or most money would always win, right? But by some miracle of nature, that’s not how it goes. And besides just being more fun think about, complex systems have many nice qualities to them.
Complexity rewards the determined. Because optimal choices emerge “randomly” in complex domains, the only way to find more optimal choices is just to spend more time in the domain (or to have someone else who has spent the time to pass them on to you). I can’t find the video now, but there was a language learning guy on Youtube who perfectly described it as: Sometimes when you watch an anime and the meaning of a word is so perfectly captured in an emotionally moving scene, and well, now the word is now just engraved in your mind. You’ll never forget it.
Complexity gives you more ways to be wrong. Wait, how is that a good thing, you ask? It’s a good thing because whatever negative thing you think about yourself or the world, you actually haven’t acquired even 1% of the evidence required to prove it. I mentioned earlier I hated statistical claims about intelligence. I’ve more or less already made my arguments against them implicitly, but I should make them more explicit.
First, intelligence is obviously changeable (at least at an individual level, which is what should matter the most to you anyway; at a societal level it’s more difficult to change simply because you can’t control other people directly), and therefore divergent, and therefore statistics is entirely the wrong tool for the job. Second, to the extent intelligence feels unchangeable, I can almost guarantee that not enough things have been tried. In this essay alone I’ve probably described about twenty specific confusions I had that got me stuck on learning various things. (And I could very easily give you another ten or twenty more from other essays I’ve written ;)) If I had jumped to the conclusion that I was just dumb instead of just missing something whenever I got stuck, I would’ve gotten absolutely nowhere.
And like, I think a lot of people have the sense that sure, childhood lead exposure reduces intelligence, but once we control for that, genetics is what really matters, except that’s just post-hoc rationalisation! You could just as easily imagine someone in the 3000s going, sure, not having your milk supplemented with Neural Growth Factor reduces intelligence, but once we control for that, genetics is what really matters. You can’t just define genetics as the residual not explained by known factors, then say “genetics” so defined means heritable factors! You’re basically just saying you don’t know what is heritable and what is not in a really obtuse way!
(There’s another bad argument for fixed intelligence that requires a bit of set up: 1) “Intelligence” obviously exists because some people are much more effective than others, and 2) “Intelligence” obviously exists because some people learn some things much faster than others. There doesn’t seem to be any contradiction until you try to teach someone ways to be more effective and they more-or-less say its pointless because they’re a slow learner. And then you point out instances where they learnt something reasonably fast and they say, sure, they learn trivial things quickly, but they must be dumb because they can’t do anything actually important right. NO! Your definition of intelligence is bad and your should feel bad! And you can’t just hold one argument in your head at a time !)
But I digress. The last thing I want to talk about is: Complexity rewards model builders. And while I would be very, very hesitant to say people in general weigh the importance of empirical evidence too heavily (because holy shit, some people believe the craziest things), if you’re somehow still reading this you probably have a pathological (and I do mean pathological, not just teehee, I just care too much about truth) need for things to be certain. Am I just describing autism? Yes, I’m just describing autism. Which, if you’re like me, you grew up immersed in an online “discourse” which, if you can’t fork out a double-blinded RCT for your claim, well, then that’s just mere speculation.
This just doesn’t work! This just EMPIRICALLY doesn’t work! There is too much to know for this to work! It’s like trying to track the position and velocity of every particle instead of tracking thermodynamic aggregates like temperature! It’s like trying to define every real number by going 0, 0.1, -0.1, 1, -1, 0.01, ... (Look, I can’t even think of a scheme that could plausibly work; the real numbers are well-known to be uncountable.) Trying to do things this way is so fundamentally unserious! If you’re going to get anything done at all, you need a model.
I slightly regret making this post a bit too technical for the average person, because I think I have a good metaphor to get across the importance of mental models. Suppose we pluck your typical lazy, under-performing, acne-riddled high school student and place them in an internet cafe (this example probably makes more sense in Asia, where internet cafes are more common, but I digress). We might be able to imagine them playing FFXIV for 16 hours straight and still be full of motivation to play more. Does planning the most optimal build or micro-ing skill activations and player positions not require mental effort? Does playing without eating or resting for 16 hours straight not require focus? So why can this dumb-ass student (cough, not me) play games so intensely but not study so intensely?
The difference lies in what the game is doing. Now, you could say, blah blah, dark patterns, blah blah, Skinner box, blah blah. And you would be wrong! Or at least right in the most trivial and uninteresting way. Because it’s implausible that you’ve never tried some dumb gacha game before that’s designed to separate you from your money, and yet you’re not (I hope) still playing it! Dark patterns aren’t voodoo. There’s something else happening, something deeper more generalisable than just flashing lights and level up sounds.
A good game is designed so that you always know what you can do next, as well as what exactly will happen if you do. That is, the difference between playing games and studying lies not in the difficulty of the task but in the player’s mental model. And if it’s extremely clear that I the player messed up by trying to block when they should’ve dodged, and they KNOW that the last item they need to craft their +3 Sword of Infinity is gated behind this STUPID-ASS boss they’ve been trying to beat for 3 f*king HOURS, then it doesn’t matter how narrow the timing of the dodge is, they’ll try again and fail again, and try again, and fail again...
Whereas if someone doesn’t know what to do, what they can even do, or what rewards they’ll get for doing it, no fucking shit they don’t feel like doing anything!
And I realise what I just said sounds a lot like the typical Redditor whining: “Oh, woe is me, Boomers had the certainty that if they just worked hard they could buy a house and raise a family and retire comfortably, whereas I us Millennials...” I don’t need to finish that damned sentence, you know how it goes. To be clear, that’s not what I’m not saying. What I’m saying is: If you don’t want to be stuck holding your hands out in front of you, blindly stumbling around in the darkness of the immediate present, only being able to react to whatever is directly in front of you, well, you better get started building your own mental model.
And might say that’s a lot of work. To which I say, is it though?
This is kind of another problem with an “evidence-based” worldview, though more in a “reinforces a bad premise” way, rather than a “directly derives from” way. You start off in primary school naively accepting whatever you’re taught and then oops, now you’ve learnt about logic and just accepting things as they are isn’t good enough for you anymore. Now, you need PROOF. Technically, you know you’re supposed to skeptically examine everything, not just new things, but that’s, like, too much work man, so in practice you just skeptically examine new things. And so the foundation upon which you build everything you will ever know... is just whatever you happened to have uncritically accepted until you first came across “23 Logical Fallacies: How to Avoid Being Wrong” or something equally inane.
...Is that even close to being theoretically justifiable?
Since I fancy myself a pragmatist, I prefer to start from what I want. Then that controls how much effort I put into figuring out whether a specific thing is true. Otherwise trying to figure out whether something is true or not is just a literal black hole (“How do mirrors reflect light?” “Wait, what is light?” “Wait, why do electrons have discrete energy levels?” “Wait, what is energy?” “Wait, why is energy conserved?” “Wait, why is energy NOT conserved?” etc.) If that’s the case then what does it even mean for model-building to be “too much work”? If model-building is the only way to get what I want, then what even is the alternative? Doing the things I want is too much work, so I’m going to do the things I don’t want?
Huh??!?!
I’m not sure about the audience who is likely reading this post, but in general I’m not too fussed about trying to convince someone who claims they’re “not smart” that they actually are, like some kind of overgrown teacher’s pet. When most adults say they’re “not smart”, what they really mean is that they’re, if not happy, then at least content with what they have and they would much rather be left alone, kthnx.
But if that’s not you, if there’s something you really, really want, there’s still an infinity of things you could try that no one else has ever tried before. And sure, it’s annoying that there’s no answer for you to just follow, and sure, there’s really way too many things (and combinations of things!) to try and most of them will do absolutely nothing. But no one who ever tried making a soccer team went like, “Oh no! I could only find one Ronaldo-tier player! I guess I’ll just give up now!” No, you fill the team with the obvious super-stars (which in this metaphor would be things like going to college for an in-demand skill), then you go down one rung of obviousness and fill in the rest, repeating until you get what you want or until the cost of getting what you want exceeds your desire to get it.
This is a slightly awkward place to stop, so I’ll just throw one more point in. One more way how a typical “evidence-based” world view is bullshit is that there’s no universal that says you can only learn (or communicate) the truth by argument. Knowing the truth is just your mind being in a state of correspondence with reality. It should be self-evident that argument is not the only way to get into that state. Living in Singapore, I often see arguments by opposition supporters along the lines of “Singaporeans are sheep who just accept whatever the government claims instead of thinking critically”, except the government has for the most part been working great and I would suspect the heuristic of “do what has always worked” has a far stronger correspondence to reality than “follow every argument through, even if they lead to absurd conclusions”. And I would like to remind everyone that when the United States forced Japan to open its ports in 1854, it did not do so by sending an flotilla of lawyers. Yet, somehow, the necessity of the Meiji Reforms was accurately conveyed.
Winning an argument is itself just a heuristic. What we’re actually trying to win is reality. And sure, it takes much longer to show reality who’s really the boss. But, like, whether you can out-argue someone who hasn’t spent 90% of their life reading dumb arguments on the internet is really besides the point. Maybe at some point in the 80s or 90s (who knows, I’m not that old ¯\_(ツ)_/¯) it was true that everyone made knowledgeable, good faith arguments, and so it was a good heuristic that the people who made the best arguments deserved the most authority. Except that shifted the meta towards making “good” arguments rather useful arguments, which filled up every large-scale communication channel with nonsense, and so the meta shifted again to down-weight mere arguments. At least, that’s what I feel I’ve been subconsciously doing.
Who knows, maybe the pendulum will swing back in favour of reasoned debate again, as a pendulum so often does. But I can’t help but feel much more emotionally stirred by a call to action like in this Palladium essay that I want to absorb into my being... :
“The only thing that matters in ‘culture’ is the ancient formula of ‘undying fame among mortals’ for great deeds of note. The great work is Achilles’ rage on the Trojan plain, Homer’s vivid account of it, the David of Michelangelo, the conquest of Mexico by Cortez, the religious inspiration of Jean d’Arc, the Principia of Newton, the steam engine of Watt, or the rocket expedition to the moon by Wernher von Braun. [...] [T]he best propaganda is the propaganda of the deed.“
...Than by yet another sophomoric argument by someone who doesn’t actually want to do anything. I suppose that’s my cue to stop indulging in writing fanciful blog posts and go back to studying actually useful things.
See you in another few months!
.png)