Understanding Recursion Fundamentals

2 hours ago 2

If for you:

Recursion is an obscure topic or you want to understand it a bit better;
Tail call and TCO are alien communication methods and;
Trampoline is a medicine name

Then this article is for you.

Here, I’ll explain what these terms are in a didactic way and the problems they solve, with examples in Ruby. But don’t worry because the examples are quite simple to understand, especially since the concepts shown here are language-agnostic.

So, come with me on this endless journey.

✋ To continue, go back to the beginning

Note: This is an English translation of the original article in Portuguese: Entendendo fundamentos de recursão

What is recursion

In computer programs, we’re used to breaking large problems into smaller problems through the use of functions or methods.

Recursion is, in an extremely simplified way, a technique in computing where these problems are broken down so that a certain function is executed recursively.

With this, the function “calls itself” to solve some computation and continue its execution.

Meet Fibo

A very classic example of recursion is discovering, given the Fibonacci sequence, or Fibo, which number is found at a certain position.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.........

With this in place, the fib function would return results like:

fib(0) = 0

fib(1) = 1

fib(2) = 1

...

fib(7) = 13

fib(10) = 55

We then have a possible recursive implementation in Ruby:

def fib(position)

return position if position < 2

fib(position - 1) + fib(position - 2)

end

This code, however, is not performant. When trying to find the number at position 10_000 (ten thousand) in the sequence, the program becomes very slow because it makes numerous redundant recursive calls.

fib(10)

/ \

fib(9) fib(8)

/ \ / \

fib(8) fib(7) fib(7) fib(6)

/ \ / \ / \

fib(7) fib(6) fib(6) fib(5) fib(6) fib(5)

/ \ / \ / \ / \

fib(6) fib(5) fib(5) fib(4) fib(5) fib(4) fib(5) fib(4)

/ \ / \ / \ / \ / \ / \ / \

...

Consequently, the larger the function input, the execution time of this code tends to grow exponentially, which in Big-O notation would be O(2^n).

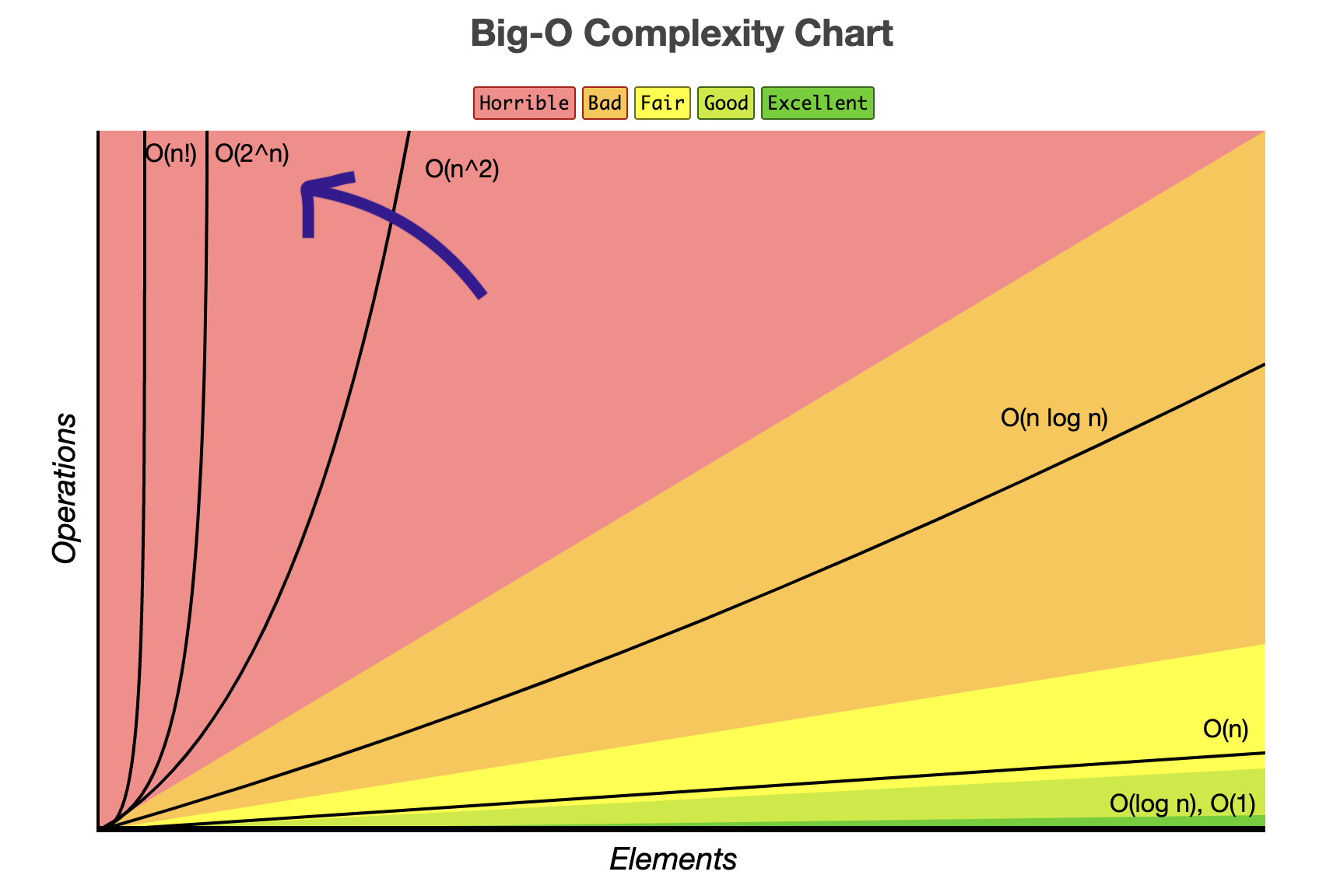
big O exponential

Is it possible to reduce this complexity?

What if we try to apply a technique where the last function call, instead of being the sum of two recursive calls, becomes just one recursive call, without performing additional computations?

This technique exists and is called tail call, or tail recursion.

Tail call

Tail call, or TC, consists of a recursive function where the last recursive call is the function itself without additional computation.

With this in place, we reduce the complexity from exponential to linear, as if it were a simple loop iterating over a list of inputs.

In Big-O notation this becomes O(n), meaning the complexity grows linearly following the growth of the input.

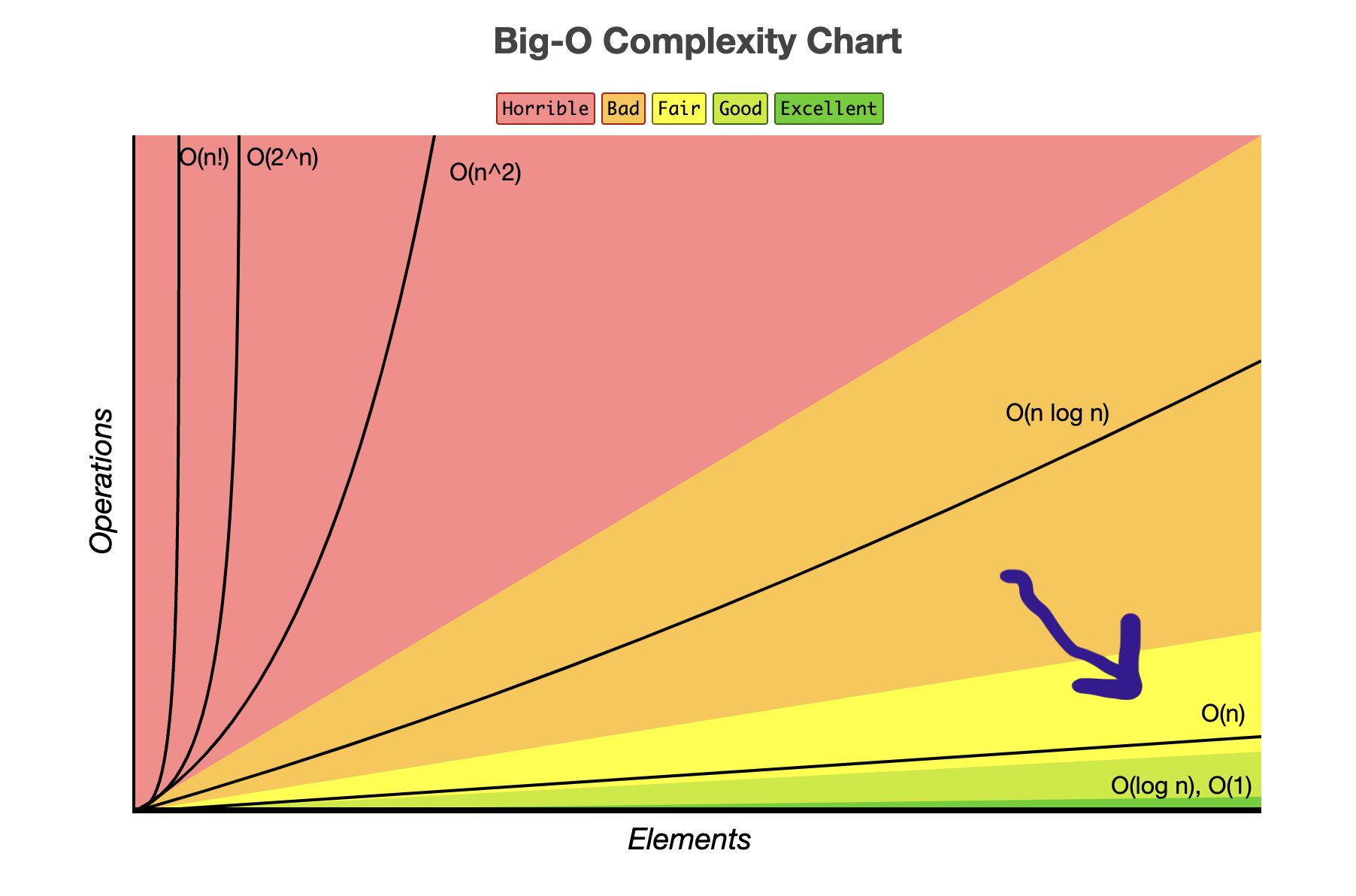
big O linear

Example in Ruby:

def fib(position, _current = 0, _next = 1)

return _current if position < 1

fib(position - 1, _next, _current + _next)

end

Therefore, the number of recursive calls is drastically reduced to something like:

fib(10, 0, 1)

fib(9, 1, 1)

fib(8, 1, 2)

fib(7, 2, 3)

fib(6, 3, 5)

fib(5, 5, 8)

fib(4, 8, 13)

fib(3, 13, 21)

fib(2, 21, 34)

fib(1, 34, 55)

fib(0, 55, 89)

Notice how the number of recursive calls decreased, meaning the code is following a more linear path with this approach.

Thus, when running the fib with TC program, the execution time is exponentially less than running without TC, being tens of thousands of times faster.

✋
Clearly a program that takes exponential time is terribly poor performance-wise, right?

# Without TC

fib(30) # 0.75 seconds

# With TC

fib(30) # 0.000075 seconds

Going back to the example of fib(10000), when running with TC, we see that execution is much faster, however:

recursion/fib.rb:10:in `fib_tc': stack level too deep (SystemStackError)

from recursion/fib.rb:10:in `fib_tc'

Uh oh, a stack overflow!

To understand what’s happening, let’s first understand what the heck is a stack and stack overflow.

Stack and stack overflow

When a program is executed, a data structure in the form of a stack, called Stack (duh), is allocated in memory and is used to store the data being used in a running function.

✋
There’s also another structure in the program’s memory called Heap, which is not a stack and has other traits that are beyond the scope of this article. To understand recursion, we focus only on the stack

When the program enters a function or method, each piece of data is pushed onto the stack. When the function finishes, the removal (pop) of each piece of data is done.

stack

With each function call, a new stack frame is assigned. Since a recursive call never ends, the runtime doesn’t know it needs to “pop” the data and finish the frame, so at every call, a new stack frame is created and more elements are added to the stack.

Guess what happens when we add too much data to the stack to the point of exceeding its limit in the computer’s memory?

Yes, the infamous Stack overflow happens 💥🪲, and this explains that error in Ruby when running fib of 10000 with tail call.

✋
So does that mean calculating fib of 10000 is an impossible problem to solve with recursion?

Hold on, some languages employ an optimization technique that consists of using the tail call with just one stack frame, hence ensuring that each recursive call is treated as if it were an iteration in a primitive loop.

With this, the function’s arguments and data are manipulated in a single stack frame, exactly as if we had written a primitive loop. And consequently, new tail recursive calls won’t cause stack overflow.

We call this technique Tail call optimization, or TCO.

Tail call optimization

Due to its imperative nature, and like several other general-purpose languages, Ruby doesn’t have native TCO support.

Usually this optimization is more commonly found in languages with a strong inclination toward the functional paradigm, rather than the imperative one.

But in Ruby it’s possible to enable TCO mode with a simple configuration in the Ruby runtime instruction (YARV), and thus we can execute fib of 10000 without pain.

RubyVM::InstructionSequence.compile_option = {

tailcall_optimization: true,

trace_instruction: false

}

def fib(position, _current = 0, _next = 1)

return _current if position < 1

fib(position - 1, _next, _current + _next)

end

# TC with TCO

fib(10000) # 0.02 seconds

Superb! With TCO enabled, a fib 10000 with tail call is executed in 0.02 seconds!

It’s worth remembering that TCO is a technique used not only in recursion but also in instruction generation optimization in compilers, but this is beyond the scope of this article.

✋
Okay, but what if it’s not possible to enable TCO for tail recursion or I’m programming in a language that doesn’t have TCO support?

Trampoline to the rescue.

Trampoline

To understand trampoline, let’s think about the problem and a possible solution.

If we think smart, we can initially conclude that recursion should be avoided, and this is premise number one.

def fib(position, _current = 0, _next = 1)

return _current if position < 1

###################################

#### We must avoid this!!!!!! ####

###################################

fib(position - 1, _next, _current + _next)

end

Premise two, instead of returning a recursive call directly, what if we return it encapsulated in an anonymous function structure that stores context to be executed in another context?

Yes, like a closure or lambda for the more attentive readers

In Ruby, we can use the concept of lambdas.

def fib(position, _current = 0, _next = 1)

return _current if position < 1

lambda do

fib(position - 1, _next, _current + _next)

end

If we call result = fib(0), because of the first line’s short-circuit (position < 1), the method’s return is 0.

But if we call result = fib(10), the return won’t be a recursive call, but rather the return will be an anonymous function (lambda).

By doing this, the method is then finished and the stack is cleared, meaning the pop of data is done from within the method.

Since lambdas store context, if we call result.call, the lambda is executed with the previous context, which can return the final number (if it enters the short-circuit) or another lambda with the new context.

And so, we loop until we have the final value, while the current return continues to be a lambda. Did you understand what we can do?

Yes, a loop!

result = fib(10000)

while result.is_a?(Proc)

result = result.call

end

puts result

Output (a really very large number):

33644764876431783266621612005107543310302148460680063906564769974680081442166662368155595513633734025582065332680836159373734790483865268263040892463056431887354544369559827491606602099884183933864652731300088830269235673613135117579297437854413752130520504347701602264758318906527890855154366159582987279682987510631200575428783453215515103870818298969791613127856265033195487140214287532698187962046936097879900350962302291026368131493195275630227837628441540360584402572114334961180023091208287046088923962328835461505776583271252546093591128203925285393434620904245248929403901706233888991085841065183173360437470737908552631764325733993712871937587746897479926305837065742830161637408969178426378624212835258112820516370298089332099905707920064367426202389783111470054074998459250360633560933883831923386783056136435351892133279732908133732642652633989763922723407882928177953580570993691049175470808931841056146322338217465637321248226383092103297701648054726243842374862411453093812206564914032751086643394517512161526545361333111314042436854805106765843493523836959653428071768775328348234345557366719731392746273629108210679280784718035329131176778924659089938635459327894523777674406192240337638674004021330343297496902028328145933418826817683893072003634795623117103101291953169794607632737589253530772552375943788434504067715555779056450443016640119462580972216729758615026968443146952034614932291105970676243268515992834709891284706740862008587135016260312071903172086094081298321581077282076353186624611278245537208532365305775956430072517744315051539600905168603220349163222640885248852433158051534849622434848299380905070483482449327453732624567755879089187190803662058009594743150052402532709746995318770724376825907419939632265984147498193609285223945039707165443156421328157688908058783183404917434556270520223564846495196112460268313970975069382648706613264507665074611512677522748621598642530711298441182622661057163515069260029861704945425047491378115154139941550671256271197133252763631939606902895650288268608362241082050562430701794976171121233066073310059947366875

🔑 Key point
And with this, friends, we have the trampoline technique: a non-recursive primitive loop that keeps calling another function written recursively but that returns a lambda with context, until reaching the final value.

This code, without TCO, for fib of 10000, takes 0.04 seconds, a result very close to TCO and without causing stack overflow.

Incredible, right? Now there are no excuses for not writing a function recursively in languages that don’t have TCO support 😛

Conclusion

In this article, the intent was to bring some concepts and fundamentals around the recursion topic. These concepts overlap with very academic topics that sometimes make it difficult for people who are starting in the field or who don’t have a very academic background to understand.

I hope I’ve clarified the recursion subject in a didactic way. If you can, leave any corrections or relevant information in the comments.