Why SSA?

If you’ve read anything about compilers in the last two decades or so, you have almost certainly heard of SSA compilers, a popular architecture featured in many optimizing compilers, including ahead-of-time compilers such as LLVM, GCC, Go, CUDA (and various shader compilers), Swift¹, and MSVC², and just-in-time compilers such as HotSpot C2³, V8⁴, SpiderMonkey⁵, LuaJIT, and the Android Runtime⁶.

SSA is hugely popular, to the point that most compiler projects no longer bother with other IRs for optimization⁷. This is because SSA is incredibly nimble at the types of program analysis and transformation that compiler optimizations want to do on your code. But why? Many of my friends who don’t do compilers often say that compilers seem like opaque magical black boxes, and SSA, as it often appears in the literature, is impenetrably complex.

But it’s not! SSA is actually very simple once you forget everything you think your programs are actually doing. We will develop the concept of SSA form, a simple SSA IR, prove facts about it, and design some optimizations on it.

note

I have previously written about the granddaddy of all modern SSA compilers, LLVM. This article is about SSA in general, and won’t really have anything to do with LLVM. However, it may be helpful to read that article to make some of the things in this article feel more concrete.

What Is SSA?

SSA is a property of intermediate representations (IRs), primarily used by compilers for optimizing imperative code that target a register machine. Register machines are computers that feature a fixed set of registers that can be used as the operands for instructions: this includes virtually all physical processors, including CPUs, GPUs, and weird tings like DSPs.

SSA is most frequently found in compiler middle-ends, the optimizing component between the frontend (which deals with the surface language programmers write, and lowers it into the middle-end’s IR), and the backend (which takes the optimized IR and lowers it into the target platform’s assembly).

SSA IRs, however, often have little resemblance to the surface language they lower out of, or the assembly language they target. This is because neither of these representations make it easy for a compiler to intuit optimization opportunities.

Imperative Code Is Hard

Imperative code consists of a sequence of operations that mutate the executing machine’s state to produce a desired result. For example, consider the following C program:

This program returns 0 no matter what its input is, so we can optimize it down to this:

But, how would you write a general algorithm to detect that all of the operations cancel out? You’re forced to keep in mind program order to perform the necessary dataflow analysis, following mutations of a and b through the program. But this isn’t very general, and traversing all of those paths makes the search space for large functions very big. Instead, you would like to rewrite the program such that a and b gradually get replaced with the expression that calculates the most recent value, like this:

Then we can replace each occurrence of a variable with its right-hand side recursively…

Then fold the constants together…

And finally, we see that we’re returning argc - argc, and can replace it with 0. All the other variables are now unused, so we can delete them.

The reason this works so well is because we took a function with mutation, and converted it into a combinatorial circuit, a type of digital logic circuit that has no state, and which is very easy to analyze. The dependencies between nodes in the circuit (corresponding to primitive operations such as addition or multiplication) are obvious from its structure. For example, consider the following circuit diagram for a one-bit multiplier:

A binary multiplier (Wikipedia)

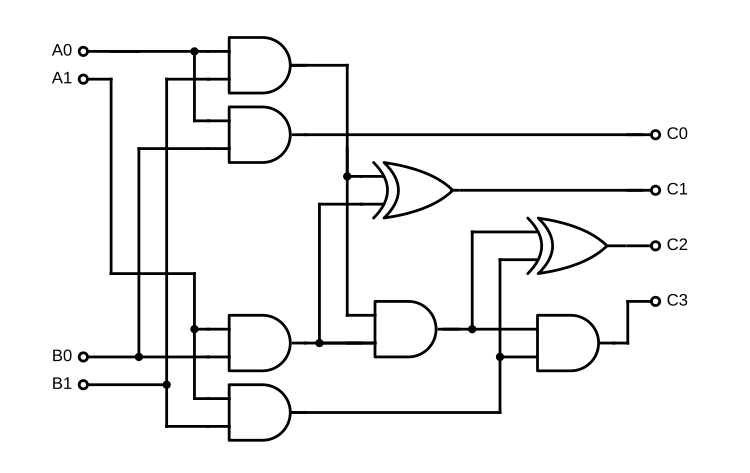
This graph representation of an operation program has two huge benefits:

1. The powerful tools of graph theory can be used to algorithmically analyze the program and discover useful properties, such as operations that are independent of each other or whose results are never used.

2. The operations are not ordered with respect to each other except when there is a dependency; this is useful for reordering operations, something compilers really like to do.

The reason combinatorial circuits are the best circuits is because they are directed acyclic graphs (DAGs) which admit really nice algorithms. For example, longest path in a graph is NP-hard (and because P≠NPP \neq NPP=NP⁸, has complexity O(2n)O(2^n)O(2n)). However, if the graph is a DAG, it admits an O(n)O(n)O(n) solution!

To understand this benefit, consider another program:

Suppose we wanted to replace each variable with its definition like we did before. We can’t just replace each constant variable with the expression that defines it though, because we would wind up with a different program!

Now, we pick up an extra y term because the squaring operation is no longer unused! We can put this into circuit form, but it requires inserting new variables for every mutation.

But we can’t do this when complex control flow is involved! So all of our algorithms need to carefully account for mutations and program order, meaning that we don’t get to use the nice graph algorithms without careful modification.

The SSA Invariant

SSA stands for “static single assignment”, and was developed in the 80s as a way to enhance the existing three-argument code (where every statement is in the form x = y op z) so that every program was circuit-like, using a very similar procedure to the one described above.

The SSA invariant states that every variable in the program is assigned to by precisely one operation. If every operation in the program is visited once, they form a combinatorial circuit. Transformations are required to respect this invariant. In circuit form, a program is a graph where operations are nodes, and “registers” (which is what variables are usually called in SSA) are edges (specifically, each output of an operation corresponds to a register).

But, again, control flow. We can’t hope to circuitize a loop, right? The key observation of SSA is that most parts of a program are circuit-like. A basic block is a maximal circuital component of a program. Simply put, it is a sequence of non-control flow operations, and a final terminator operation that transfers control to another basic block.

The basic blocks themselves form a graph, the control flow graph, or CFG. This formulation of SSA is sometimes called SSA-CFG⁹. This graph is not a DAG in general; however, separating the program into basic blocks conveniently factors out the “non-DAG” parts of the program, allowing for simpler analysis within basic blocks.

There are two equivalent formalisms for SSA-CFG. The traditional one uses special “phi” operations (often called phi nodes, which is what I will call them here) to link registers across basic blocks. This is the formalism LLVM uses. A more modern approach, used by MLIR, is block arguments: each basic block specifies parameters, like a function, and blocks transferring control flow to it must pass arguments of those types to it.

My First IR

Let’s look at some code. First, consider the following C function which calculates Fibonacci numbers using a loop.

How might we express this in an SSA-CFG IR? Let’s start inventing our SSA IR! It will look a little bit like LLVM IR, since that’s what I’m used to looking at.

Every block ends in a goto, which transfers control to one of several possible blocks. In the process, it calls that block with the given arguments. One can think of a basic block as a tiny function which tails¹⁰ into other basic blocks in the same function.

asidePhi Nodes

LLVM IR is… older, so it uses the older formalism of phi nodes. “Phi” comes from “phony”, because it is an operation that doesn’t do anything; it just links registers from predecessors.

A phi operation is essentially a switch-case on the predecessors, each case selecting a register from that predecessor (or an immediate). For example, @loop.start has two predecessors, the implicit entry block @entry, and @loop.body. In a phi node IR, instead of taking a block argument for %n, it would specify

The value of the phi operation is the value from whichever block jumped to this one.

This can be awkward to type out by hand and read, but is a more convenient representation for describing algorithms (just “add a phi node” instead of “add a parameter and a corresponding argument”) and for the in-memory representation, but is otherwise completely equivalent.

It’s a bit easier to understand the transformation from C to our IR if we first rewrite the C to use goto instead of a for loop:

However, we still have mutation in the picture, so this isn’t SSA. To get into SSA, we need to replace every assignment with a new register, and somehow insert block arguments…

Entering SSA Form

The above IR code is already partially optimized; the named variables in the C program have been lifted out of memory and into registers. If we represent each named variable in our C program with a pointer, we can avoid needing to put the program into SSA form immediately. This technique is used by frontends that lower into LLVM, like Clang.

We’ll enhance our IR by adding a stack declaration for functions, which defines scratch space on the stack for the function to use. Each stack slot produces a pointer that we can load from and store to.

Our Fibonacci function would now look like so:

Any time we reference a named variable, we load from its stack slot, and any time we assign it, we store to that slot. This is very easy to get into from C, but the code sucks because it’s doing lots of unnecessary pointer operations. How do we get from this to the register-only function I showed earlier?

asideProgram Order

We want program order to not matter for the purposes of reordering, but as we’ve written code here, program order does matter: loads depend on prior stores but stores don’t produce a value that can be used to link the two operations.

We can restore not having program order by introducing operands representing an “address space”; loads and stores take an address space as an argument, and stores return a new address space. An address space, or mem, represents the state of some region of memory. Loads and stores are independent when they are not connected by a mem argument.

This type of enhancement is used by Go’s SSA IR, for example. However, it adds a layer of complexity to the examples, so instead I will hand-wave this away.

The Dominance Relation

Now we need to prove some properties about CFGs that are important for the definition and correctness of our optimization passes.

First, some definitions.

definition

The predecessors (or “preds”) of a basic block is the set of blocks with an outgoing edge to that block. A block may be its own predecessors.

Some literature calls the above “direct” or immediate predecessors. For example, the preds of in our example are @loop.start are @entry (the special name for the function entry-point) @loop.body.

definition

The successors (no, not “succs”) of a basic block is the set of blocks with an outgoing edge from that block. A block may be its own successors.

The sucessors of @loop.start are @exit and @loop.body. The successors are listed in the loop’s goto.

If a block @a is a transitive pred of a block @b, we say that @a weakly dominates @b, or that it is a weak dominator of @b. For example, @entry, @loop.start and @loop.body both weakly dominate @exit.

However, this is not usually an especially useful relationship. Instead, we want to speak of dominators:

definition

A block @a is a dominator (or dominates) @b if every pred of @b is dominated by @a, or if @a is @b itself.

Equivalently, the dominator set of @b is the intersection of the dominator sets of its preds, plus @b.

The dominance relation has some nice order properties that are necessary for defining the core graph algorithms of SSA.

Some Graph Theory

We only consider CFGs which are flowgraphs, that is, all blocks are reachable from the root block @entry, which has no preds. This is necessary to eliminate some pathological graphs from our proofs. Importantly, we can always ask for an acyclic path¹¹ from @entry to any block @b.

An equivalent way to state the dominance relationship is that from every path from @entry to @b contains all of @b’s dominators.

proposition

@a dominates @b iff every path from @entry to @b contains @a.

proof

First, assume every @entry to @b path contains @a. If @b is @a, we’re done. Otherwise we need to prove each predecessor of @b is dominated by @a; we do this by induction on the length of acyclic paths from @entry to @b. Consider preds @p of @b that are not @a, and consider all acyclic paths ppp from @entry to @p; by appending @b to them, we have an acyclic path p′p'p′ from @entry to @b, which must contain @a. Because both the last and second-to-last elements of this are not @a, it must be within the shorter path ppp which is shorter than p′p'p′. Thus, by induction, @a dominates @p and therefore @b

Going the other way, if @a dominates @b, and consider a path ppp from @entry to @b. The second-to-last element of ppp is a pred @p of @b; if it is @a we are done. Otherwise, we can consider the path ppp made by deleting @b at the end. @p is dominated by @a, and p′p'p′ is shorter than ppp, so we can proceed by induction as above.

Onto those nice properties. Dominance allows us to take an arbitrarily complicated CFG and extract from it a DAG, composed of blocks ordered by dominance.

theorem

The dominance relation is a partial order.

proof

Dominance is reflexive and transitive by definition, so we only need to show blocks can’t dominate each other.

Suppose distinct @a and @b dominate each other.Pick an acyclic pathppp from @entry to @a. Because @b dominates @a, there is a prefix p′p'p′ of this path ending in @b. But because @a dominates @b, some prefix p′′p''p′′ of p′p'p′ ends in @a. But now ppp must contain @a twice, contradicting that it is acyclic.

This allows us to write @a < @b when @a dominates @b. There is an even more refined graph structure that we can build out of dominators, which follows immediately from the partial order theorem.

corollary

The dominators of a basic block are totally ordered by the dominance relation.

proof

Suppose @a1 < @b and @a2 < @b, but neither dominates the other. Then, there must exist acyclic paths from @entry to @b which contain both, but in different orders. Take the subpaths of those paths which follow @entry ... @a1, and @a1 ... @b, neither of which contains @a2. Concatenating these paths yields a path from @entry to @b that does not contain @a2, a contradiction.

This tells us that the DAG we get from the dominance relation is actually a tree, rooted at @entry. The parent of a node in this tree is called its immediate dominator.

Computing dominators can be done iteratively: the dominator set of a block @b is the intersection the dominator sets of its preds, plus @b. This algorithm runs in quadratic time.

A better algorithm is the Lengauer-Tarjan algorithm[^lta]. It is relatively simple, but explaining how to implement it is a bit out of scope for this article. I found a nice treatment of it here.

What’s important is we can compute the dominator tree without breaking the bank, and given any node, we can ask for its immediate dominator. Using immediate dominators, we can introduce the final, important property of dominators.

definition

The dominance frontier of a block @a is the set of all blocks not dominated by @a with at least one pred which @a dominates.

These are points where control flow merges from distinct paths: one containing @a and one not. The dominance frontier of @loop.body is @loop.start, whose preds are @entry and @loop.body.

There are many ways to calculate dominance frontiers, but with a dominance tree in hand, we can do it like this:

algorithmDominance Frontiers.

For each block @b with more than one pred, for each of its preds, let @p be that pred. Add @b to the dominance frontier of @p and all of its dominators, stopping when encountering @b’ immediate dominator.

proof

We need to prove that every block examined by the algorithm winds up in the correct frontiers.

First, we check that every examined block @b is added to the correct frontier. If @a < @p, where @p is a pred of @b, and a @d is @b’s immediate dominator, then if @a < @d, @b is not in its frontier, because @a must dominate @b. Otherwise, @b must be in @a’s frontier, because @a dominates a pred but it cannot dominate @b, because then it would be dominated by @i, a contradiction.

Second, we check that every frontier is complete. Consider a block @a. If an examined block @b is in its frontier, then @a must be among the dominators of some pred @p, and it must be dominated by @b’s immediate dominator; otherwise, @a would dominate @b (and thus @b would not be in its frontier). Thus, @b gets added to @a’s dominator.

You might notice that all of these algorithms are quadratic. This is actually a very good time complexity for a compilers-related graph algorithm. Cubic and quartic algorithms are not especially uncommon, and yes, your optimizing compiler’s time complexity is probably cubic or quartic in the size of the program!

Lifting Memory

Ok. Let’s construct an optimization. We want to figure out if we can replace a load from a pointer with the most recent store to that pointer. This will allow us to fully lift values out of memory by cancelling out store/load pairs.

This will make use of yet another implicit graph data structure.

definition

The dataflow graph is the directed graph made up of the internal circuit graphs of each each basic block, connected along block arguments.

To follow a use-def chain is to walk this graph forward from an operation to discover operations that potentially depend on it, or backwards to find operations it potentially depends on.

It’s important to remember that the dataflow graph, like the CFG, does not have a well defined “up” direction. Navigating it and the CFG requires the dominator tree.

One other important thing to remember here is that every instruction in a basic block always executes if the block executes. In much of this analysis, we need to appeal to “program order” to select the last load in a block, but we are always able to do so. This is an important property of basic blocks that makes them essential for constructing optimizations.

Forward Dataflow

For a given store %p, %v, we want to identify all loads that depend on it. We can follow the use-def chain of %p to find which blocks contain loads that potentially depend on the store (call it %s).

First, we can eliminate loads within the same basic block (call it @a). Replace all load %p instructions after s (but before any other store %p, _s, in program order) with %v’s def. If s is not the last store in this block, we’re done.

Otherwise, follow the use-def chain of %p to successors which use %p, i.e., successors whose goto case has %p as at least one argument. Recurse into those successors, and now replacing the pointer %p of interest with the parameters of the successor which were set to %p (more than one argument may be %p).

If successor @b loads from one of the registers holding %p, replace all such loads before a store to %p. We also now need to send %v into @b somehow.

This is where we run into something of a wrinkle. If @b has exactly one predecessor, we need to add a new block argument to pass whichever register is holding %v (which exists by induction). If %v is already passed into @b by another argument, we can use that one.

However, if @b has multiple predecessors, we need to make sure that every path from @a to @b sends %v, and canonicalizing those will be tricky. Worse still, if @b is in @a’s domination frontier, a different store could be contributing to that load! For this reason, dataflow from stores to loads is not a great strategy.

Instead, we’ll look at dataflow from loads backwards to stores (in general, dataflow from uses to defs tends to be more useful), which we can use to augment the above forward dataflow analysis to remove the complex issues around domination frontiers.

Dependency Analysis

Let’s analyze loads instead. For each load %p in @a, we want to determine all stores that could potentially contribute to its value. We can find those stores as follows:

We want to be able to determine which register in a given block corresponds to the value of %p, and then find its last store in that block.

To do this, we’ll flood-fill the CFG backwards in BFS order. This means that we’ll follow preds (through the use-def chain) recursively, visiting each pred before visiting their preds, and never revisiting a basic block (except we may need to come back to @a at the end).

Determining the “equivalent”¹² of %p in @b (we’ll call it %p.b) can be done recursively: while examining @b, follow the def of %p.b. If %p.b is a block parameter, for each pred @c, set %p.c to the corresponding argument in the @b(...) case in @c’s goto.

Using this information, we can collect all stores that the load potentially depends on. If a predecessor @b stores to %p.b, we add the last such store in @b (in program order) to our set of stores, and do not recurse to @b’s preds (because this store overwrites all past stores). Note that we may revisit @a in this process, and collect a store to %p from it occurs in the block. This is necessary in the case of loops.

The result is a set stores of (store %p.s %v.s, @s) pairs. In the process, we also collected a set of all blocks visited, subgraph, which are dominators of @a which we need to plumb a %v.b through. This process is called memory dependency analysis, and is a key component of many optimizations.

note

Not all contributing operations are stores. Some may be references to globals (which we’re disregarding), or function arguments or the results of a function call (which means we probably can’t lift this load). For example %p gets traced all the way back to a function argument, there is a code path which loads from a pointer whose stores we can’t see.

It may also trace back to a stack slot that is potentially not stored to. This means there is a code path that can potentially load uninitialized memory. Like LLVM, we can assume this is not observable behavior, so we can discount such dependencies. If all of the dependencies are uninitialized loads, we can potentially delete not just the load, but operations which depend on it (reverse dataflow analysis is the origin of so-called “time-traveling” UB).

Lifting Loads

Now that we have the full set of dependency information, we can start lifting loads. Loads can be safely lifted when all of their dependencies are stores in the current function, or dependencies we can disregard thanks to UB in the surface language (such as null loads or uninitialized loads).

note

There is a lot of fuss in this algorithm about plumbing values through block arguments. A lot of IRs make a simplifying change, where every block implicitly receives the registers from its dominators as block arguments.

I am keeping the fuss because it makes it clearer what’s going on, but in practice, most of this plumbing, except at dominance frontiers, would be happening in the background.

Suppose we can safely lift some load. Now we need to plumb the stored values down to the load. For each block @b in subgraph (all other blocks will now be in subgraph unless stated otherwise). We will be building two mappings: one (@s, @b) -> %v.s.b, which is the register equivalent to %v.s in that block. We will also be building a map @b -> %v.b, which is the value that %p must have in that block.

1. Prepare a work queue, with each @s in it initially.

2. Pop a block @a form the queue. For each successor @b (in subgraph):

   1. If %v.b isn’t already defined, add it as a block argument. Have @a pass %v.a to that argument.

   2. If @b hasn’t been visited yet, and isn’t the block containing the load we’re deleting, add it to the queue.

Once we’re done, if @a is the block that contains the load, we can now replace all loads to %p before any stores to %p with %v.a.

tip

There are cases where this whole process can be skipped, by applying a “peephole” optimization. For example, stores followed by loads within the same basic block can be optimized away locally, leaving the heavy-weight analysis for cross-block store/load pairs.

Worked Example

Here’s the result of doing dependency analysis on our Fibonacci function. Each load is annotated with the blocks and stores in stores.

Let’s look at L1. Is contributing loads are in @entry and @loop.body. So we add a new parameter %n: in @entry, we call that parameter with %n (since that’s stored to it in @entry), while in @loop.body, we pass %n.2.

What about L4? The contributing loads are also in @entry and @loop.body, but one of those isn’t a pred of @exit. @loop.start is also in the subgraph for this load, though. So, starting from @entry, we add a new parameter %a to @loop.body and feed 0 (the stored value, an immediate this time) through it. Now looking at @loop.body, we see there is already a parameter for this load (%a), so we just pass %b as that argument. Now we process @loop.start, which @entry pushed onto the queue. @exit gets a new parameter %a, which is fed @loop.start’s own %a. We do not re-process @loop.body, even though it also appears in @loop.start’s gotos, because we already visited it.

After doing this for the other two loads, we get this:

After lifting, if we know that a stack slot’s pointer does not escape (i.e., none of its uses wind up going into a function call¹³) or a write to a global (or a pointer that escapes), we can delete every store to that pointer. If we delete every store to a stack slot, we can delete the stack slot altogether (there should be no loads left for that stack slot at this point).

Complications

This analysis is simple, because it assumes pointers do not alias in general. Alias analysis is necessary for more accurate dependency analysis. This is necessary, for example, for lifting loads of fields of structs through subobject pointers, and dealing with pointer arithmetic in general.

However, our dependency analysis is robust to passing different pointers as arguments to the same block from different predecessors. This is the case that is specifically handled by all of the fussing about with dominance frontiers. This robustness ultimately comes from SSA’s circuital nature.

Similarly, this analysis needs to be tweaked to deal with something like select %cond, %a, %b (a ternary, essentially). selects of pointers need to be replaced with selects of the loaded values, which means we need to do the lifting transformation “all at once”: lifting some liftable loads will leave the IR in an inconsistent state, until all of them have been lifted.

Cleanup Passes

Many optimizations will make a mess of the CFG, so it’s useful to have simple passes that “clean up” the mess left by transformations. Here’s some easy examples.

Unused Result Elimination

If an operation’s result has zero uses, and the operation has no side-effects, it can be deleted. This allows us to then delete operations that it depended on that now have no side effects. Doing this is very simple, due to the circuital nature of SSA: collect all instructions whose outputs have zero uses, and delete them. Then, examine the defs of their operands; if those operations now have no uses, delete them, and recurse.

This bubbles up all the way to block arguments. Deleting block arguments is a bit trickier, but we can use a work queue to do it. Put all of the blocks into a work queue.

1. Pop a block from the queue.

2. Run unused result elimination on its operations.

3. If it now has parameters with no uses, remove those parameters.

4. For each pred, delete the corresponding arguments to this block. Then, Place those preds into the work queue (since some of their operations may have lost their last use).

5. If there is still work left, go to 1.

Simplifying the CFG

There are many CFG configurations that are redundant and can be simplified to reduce the number of basic blocks.

For example, unreachable code can help delete blocks. Other optimizations may cause the goto at the end of a function to be empty (because all of its successors were optimized away). We treat an empty goto as being unreachable (since it has no cases!), so we can delete every operation in the block up to the last non-pure operation. If we delete every instruction in the block, we can delete the block entirely, and delete it from its preds’ gotos. This is a form of dead code elimination, or DCE, which combines with the previous optimization to aggressively delete redundant code.

Some jumps are redundant. For example, if a block has exactly one pred and one successor, the pred’s goto case for that block can be wired directly to the successor. Similarly, if two blocks are each other’s unique predecessor/successor, they can be fused, creating a single block by connecting the input blocks’ circuits directly, instead of through a goto.

If we have a ternary select operation, we can do more sophisticated fusion. If a block has two successors, both of which the same unique successor, and those successors consist only of gotos, we can fuse all four blocks, replacing the CFG diamond with a select. In terms of C, this is this transformation:

LLVM’s CFG simplification pass is very sophisticated and can eliminate complex forms of control flow.

Conclusion

I am hoping to write more about SSA optimization passes. This is a very rich subject, and viewing optimizations in isolation is a great way to understand how a sophisticated optimization pipeline is built out of simple, dumb components.

It’s also a practical application of graph theory that shows just how powerful it can be, and (at least in my opinion), is an intuitive setting for understanding graph theory, which can feel very abstract otherwise.

In the future, I’d like to cover CSE/GVN, loop optimizations, and, if I’m feeling brave, getting out of SSA into a finite-register machine (backends are not my strong suit!).