Basic idea
Zipf's Law describes a power law distribution that appears across numerous natural phenomena. The concept is elegantly simple: when you rank items by their frequency or size, the relationship follows a predictable pattern.
Here's how it works: if you arrange items in descending order by their frequency, the Nth item will occur approximately 1/N times as often as the most frequent item. Mathematically, this means:
- The 1st ranked item has frequency X₁
- The 2nd ranked item has frequency X₁/2
- The 3rd ranked item has frequency X₁/3
- The Nth ranked item has frequency X₁/N
This creates a smooth, curved distribution when plotted on a graph, revealing an underlying order in what might initially appear random.
Occurences
Human Language
The most famous application of Zipf's Law is in linguistics. In English, "the" is the most common word, appearing about 7% of the time. "Of" (the second most common) appears roughly half as often at 3.5%. "And" (third) appears about 2.3% of the time. This pattern continues remarkably consistently across languages.
This discovery led linguists to propose Zipf's Law as a litmus test for determining whether a language is artificial or naturally evolved. Real human languages follow this distribution almost universally, while constructed languages often deviate from it.
City Populations
Urban demographics also follow Zipf's Law. In the United States, New York City is the largest with about 8.3 million people. Los Angeles (second largest) has roughly 4 million—close to half. Chicago (third) has about 2.7 million. This pattern holds across countries and time periods.
Passwords
Even in cybersecurity, Zipf's Law emerges. Password frequency distributions follow this pattern, with the most common passwords appearing exponentially more often than less common ones. This has significant implications for security analysis and breach prevention.
The Deeper Implication
These occurrences hint at an emergent deeper pattern governing self-organizing natural systems. When complex systems evolve without central planning—whether languages, cities, or digital behaviors—they tend to organize themselves according to this mathematical principle.
Relativation: it occurs also for randomly generated words
"In conclusion, Zipf's law is not a deep law in natural language as one might first have thought. It is very much related the particular representation one chooses, i.e., rank as the independent variable." (1) -> Hinting again at a deeper pattern: the observer is part of the observation - the world is inherently subjective and will always look different depending how you look at it.
I added an attractor based probability distribution (words that have occurred before are more likely to be sampled, which produces a smoother Zipf curve fit - hinting at attraction effects in natural processes?)
import random
import matplotlib.pyplot as plt
from collections import Counter
import numpy as np
from scipy import stats
attractor_strength = 1.11
ALPHABET = ['a', 'b', 'c', 'd', 'e', '_']
def calculate_dynamic_attractor_probability(total_words, base_prob=0.16, growth_rate=0.0008, max_prob=0.9):
"""Calculate dynamic attractor probability based on total words generated"""
dynamic_prob = base_prob + (max_prob - base_prob) * (1 - np.exp(-growth_rate * total_words))
return min(dynamic_prob, max_prob)
def generate_attractor_text(alphabet, num_chars=100000):
"""Generate random text with dynamic attractor mechanism - probability increases with word count"""
words = []
word_counts = {}
text = ''.join(random.choices(alphabet, k=num_chars // 10))
initial_words = [word for word in text.split('_') if word]
for word in initial_words:
words.append(word)
word_counts[word] = word_counts.get(word, 0) + 1
target_length = len(initial_words) * 10
prob_checkpoints = [len(words) * i // 10 for i in range(1, 11)]
while len(words) < target_length:
current_attractor_prob = calculate_dynamic_attractor_probability(len(words))
if len(words) in prob_checkpoints:
print(f"Words generated: {len(words)}, Attractor probability: {current_attractor_prob:.3f}")
if word_counts and random.random() < current_attractor_prob:
word_list = list(word_counts.keys())
weights = [word_counts[word] ** attractor_strength for word in word_list]
chosen_word = random.choices(word_list, weights=weights, k=1)[0]
words.append(chosen_word)
word_counts[chosen_word] += 1
else:
word_length = random.randint(1, 5)
new_word = ''.join(random.choices(alphabet[:-1], k=word_length))
if new_word:
words.append(new_word)
word_counts[new_word] = word_counts.get(new_word, 0) + 1
return words
def generate_li_uniform_text(alphabet, num_chars=100000):
"""Generate random text with uniform character probabilities"""
text = ''.join(random.choices(alphabet, k=num_chars))
words = [word for word in text.split('_') if word]
return words
def calculate_zipf_slope(ranks, frequencies):
"""Calculate Zipf slope using linear regression on log-log scale"""
log_ranks = np.log10(ranks)
log_freqs = np.log10(frequencies)
valid = np.isfinite(log_ranks) & np.isfinite(log_freqs)
if np.sum(valid) < 2:
return None, None
slope, _, r_value, _, _ = stats.linregress(log_ranks[valid], log_freqs[valid])
return slope, r_value**2
def plot_attractor_experiment():
"""Generate and plot attractor experiment with uniform comparison"""
print("Generating attractor mechanism experiment with uniform comparison...")
uniform_words = generate_li_uniform_text(ALPHABET)
attractor_words = generate_attractor_text(ALPHABET)
print(f"Generated {len(uniform_words)} uniform words and {len(attractor_words)} attractor words")
uniform_counts = Counter(uniform_words).most_common(1000)
attractor_counts = Counter(attractor_words).most_common(1000)
uniform_ranks = np.array(range(1, len(uniform_counts) + 1))
uniform_freqs = np.array([count for _, count in uniform_counts])
attractor_ranks = np.array(range(1, len(attractor_counts) + 1))
attractor_freqs = np.array([count for _, count in attractor_counts])
uniform_slope, uniform_r2 = calculate_zipf_slope(uniform_ranks, uniform_freqs)
attractor_slope, attractor_r2 = calculate_zipf_slope(attractor_ranks, attractor_freqs)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
ax1.loglog(uniform_ranks, uniform_freqs, 'go-', alpha=0.7, markersize=3,
label='Uniform probabilities')
if uniform_slope:
fitted_line = uniform_freqs[0] * (uniform_ranks ** uniform_slope)
ax1.loglog(uniform_ranks, fitted_line, 'r--', alpha=0.8,
label=f'Slope: {uniform_slope:.3f} (R²={uniform_r2:.3f})')
ax1.set_xlabel('Rank')
ax1.set_ylabel('Frequency')
ax1.set_title('Uniform Character Probabilities\n(Strong Step Pattern)')
ax1.grid(True, alpha=0.3)
ax1.legend()
ax2.loglog(attractor_ranks, attractor_freqs, 'mo-', alpha=0.7, markersize=3,
label='Attractor mechanism')
if attractor_slope:
fitted_line = attractor_freqs[0] * (attractor_ranks ** attractor_slope)
ax2.loglog(attractor_ranks, fitted_line, 'r--', alpha=0.8,
label=f'Slope: {attractor_slope:.3f} (R²={attractor_r2:.3f})')
ax2.set_xlabel('Rank')
ax2.set_ylabel('Frequency')
ax2.set_title('Attractor Mechanism - Zipf Law Distribution\n(Smoother Pattern)')
ax2.grid(True, alpha=0.3)
ax2.legend()
plt.tight_layout()
plt.show()
print(f"\nResults:")
uniform_slope_str = f"{uniform_slope:.4f}" if uniform_slope is not None else "N/A"
uniform_r2_str = f"{uniform_r2:.4f}" if uniform_r2 is not None else "N/A"
attractor_slope_str = f"{attractor_slope:.4f}" if attractor_slope is not None else "N/A"
attractor_r2_str = f"{attractor_r2:.4f}" if attractor_r2 is not None else "N/A"
print(f"Uniform case: slope = {uniform_slope_str}, R² = {uniform_r2_str}")
print(f"Attractor case: slope = {attractor_slope_str}, R² = {attractor_r2_str}")
print(f"\nKey finding: The attractor mechanism creates a stronger Zipf-like distribution")
print(f"compared to uniform probabilities, demonstrating preferential attachment effects.")
plot_attractor_experiment()
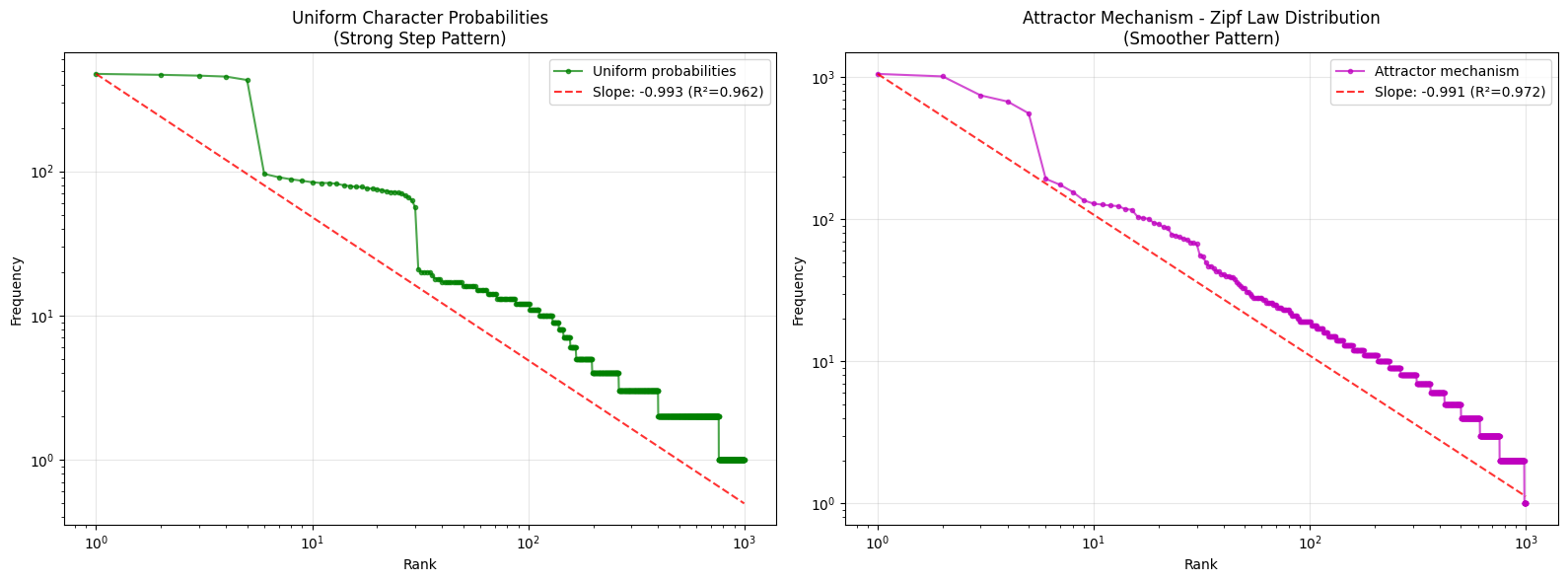
Closer examination: or does it?
"It is shown that real texts fill the lexical spectrum much more efficiently and regardless of the word length, suggesting that the meaningfulness of Zipf’s law is high." (2) -> Seems Zipf's law is after all not so easily explained...?
References
#idea #programming

.png)



