Are Electromagnetic Waves Real?

Photo by Francisco Cornellana Castells

From the right perspective, the 19th century looked like an explosion.

An explosion of science and technology, to be specific. Steam engines, combustion engines, photography, lightbulbs, telephones, statistical mechanics, thermodynamics, electrodynamics and, most importantly, coca-cola.

With one technological marvel after another, it’s no wonder that the period became the inspiration for the fantastical steampunk genre. And when it come down to role playing, few did the part of the main character as well as James Clerk Maxwell.

Setting the kinematical and statistical grounds for thermodynamics, as he did, was easily worth several lifetimes of effort by mere mortals (as we’ve seen here). However, he wasn’t satisfied with that and also decided to also solve electromagnetism once and for all. I swear, the dude was playing on easy mode.

Eventually, he performed a speedrun of the problems regarding electricity and magnetism, arriving at a unified model for both and calling it just another Tuesday. However, for a model to be truly impressive, it must predict things yet not seen or understood.

In this, Maxwell did not disappoint. As ripples from a rock thrown into a pond, waves emerged from the mathematics of his work. Their speed, he argued, was eerily similar to that of light and so, light it had to be.

This was a profound result, alas, a mathematical one and we know that maths can be full of elegant artifacts, which find no purchase in reality. The speed of the waves akin to that of light was a very strong argument for the validity of the model, but not definitive proof. After all, it could’ve been just a terrible coincidence.

At the time, Maxwell’s work (check here), though potentially groundbreaking, was seen as unvalidated. Such was the case for about 20 years.

Then, Heinrich Rudolf Hertz came along.

Heinrich is a name that managed to go down not quite well in history, even though Hertz brought it much honor to start with. From a young age the lad was trained to be an intellectual übermensch. Private tutoring, watched closely by his mother, all that stuff. He was good that everything he did, woodworking, engineering and, shockingly, physics.

He was so good that, despite little experience and formal education, he was taken on as a student by Hermann von Helmholtz. Being a physics titan, we’ve seen Helmholtz making cameos in different parts here in Physics Rediscovered, but haven’t given him the proper attention, yet (subject to change).

Just like his old man of a tutor, young Hertz was fascinated with electromagnetism. Helmholtz was trying and failing to conduct meaningful experiments (in)validating Maxwell’s theory. However, being the influential man that he was, he established the “Berlin prize” for anyone who could come up with the right tests.

With so much expectations from the promising Hertz, you could imagine the man’s frustration and the weight of pressure when in 1882 the “Berlin prize” expired unclaimed. Based on some entries from his diary (from 1884) we can have a glimpse into how he felt:

8 July. Electromagnetics, still without success.

17 July. Depressed; could not get on with anything.

24 July. Did not feel like working.

7 August. Saw from Ries’s book that most of what I have found so far is already known.

Resonates with anyone?

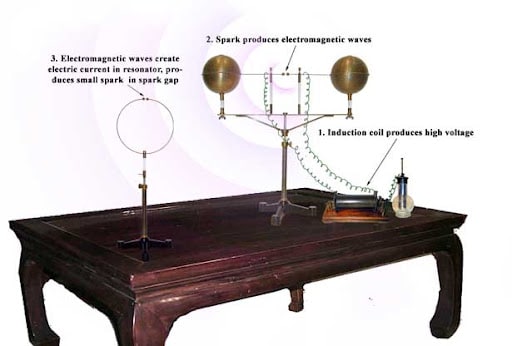
Such was his state of mind when he was teaching at the Technische Hochschule in Karlsruhe. While lecturing his students about sparks, he experimented with a Riess (or Knochenhauer) spirals. The contraption looked similar to this one:

As can be found in the Science Museum in London

The two discs contain spiral wires and never touch one another. What Hertz noticed is that when you create a spark between the terminals of one of the disc, another spark flashes between the terminals of the other one.

Very, very reliable sources tell us that Hertz’s reaction was: Huh… In fact, this is one of the most important thoughts that a scientist can have. It usually signifies the beginning of something extraordinary.

Indeed, such was the case with Hertz. At the time no one really knew how to produce electromagnetic waves at will or if it was even possible. However, he figured that if Maxwell’s theory was supposed to be correct, then such waves should travel between the separated spirals. If they did, then he was gonna ride them like a surfer of the aether.

However, in order to do that he needed something better than the Riess spirals. It had to be stronger and mobile, so that he could catch the waves wherever they may be, even very weak ones. Inspired by the spirals he came up with something like this:

As can be found in the Spark Museum in Bellingham, Washington. The place looks awesome.

Here’s how it should work:

The jar and coil on the right provide the electricity. The two large spheres in the middle serve as the wave generator. One of the spheres is charged and eventually builds up so much potential that, at some point, creates a spark that travels between the two small terminals between the spheres. The other sphere takes on some of that charge and fires back, again with a spark. The whole thing oscillates until the charges equalize.

Now, the thing on the left, that looks like an incredibly brave piercing item, will be the receiver. The sparks between the spheres should produce electric and magnetic fields in form of a wave and these should induce a current on that bull ring, which should be visible as sparks between its own terminals.

Hopefully.

He started off with simply trying to get a spark on the receiver and was successful. It wasn’t effortless though as the induced spark was very small and short lived. The experiment had to be conducted in total darkness, which made positioning the receiver and taking notes somewhat awkward. Overall, a good start but nothing new. This was simply the well known induction effect and no indication of a wave being involved.

So how does a man find an invisible wave? A man needs a name, but can also ask: what do waves do? Well, they reflect from surfaces, for example.

Hertz decided to try reflections but contemplated becoming a faceless assassin as a plan B, in case the whole experiment didn’t pan out.

Mirrors seem to make good reflecting surfaces so he placed one at an angle, with respect the emitting spheres, to redirect the alleged wave somewhere else. Without a mirror he did not catch a spark on his bull ring. However, with a mirror:

Ok, so whatever this is, seems to be reflecting off of surfaces like a wave would. This is already very promising, but not definitive. After all, balls tend to bounce off surfaces like waves would so maybe these electromagnetic signals are just small ball-like particles?

Just like Hertz did, we need to press the issue further.

Another thing people knew about waves back then is that they like to refract. That means they like to bend when passing between different mediums.

This is exactly what we see when we pass light through a prism and witness the rainbow on the other end, made possible by each color bending somewhat different then the one next to it. Newton already exhausted the issue during the copious amount of spare time he had back when England was being consumed the plague. Here’s a friendly reminder:

Inspired by Newton, Hertz fired up the generator again, but this time replaced the mirror with a prism. Setting the receiver to the side, he observer no sparks without the prism. However, with one:

Ok, this is it right? I mean, the thing bends like a wave would so what the hell?!

I know that by now you can barely hold it in, gentle reader, but this is not yet the smoking gun Hertz was looking for.

You see, light being particles was an idea strongly advocated by Newton. He suggested that as these particles might interact (maybe gravitationally) with those of matter as they pass through an object and bend their trajectories as a result. Since he was the OG physics influencer, he couldn’t be dismissed right away.

There is one more thing we can try, but this one will require some getting used to.

See, waves allowed Hertz to perform this special trick. He could make a pencil disappear, but he could also make them stand in a very special way. His non-contemporaries tell us that terrorizing the streets of Gotham was his plan C, in case the experiment went south.

So how’s the trick done?

Well, first consider the shape of a wave. It’s usually represented by a sine or cosine function. Let’s take cosine because why not. The trouble with cosine is that it only goes from -1 to 1 and what if we wanted our wave to reach up to 12 or even 57? We should add a scaling factor to that cosine to make that possible. Let’s call it A. So far our wave is:

Here, α is the dimensionless argument of the cosine and can be whatever.

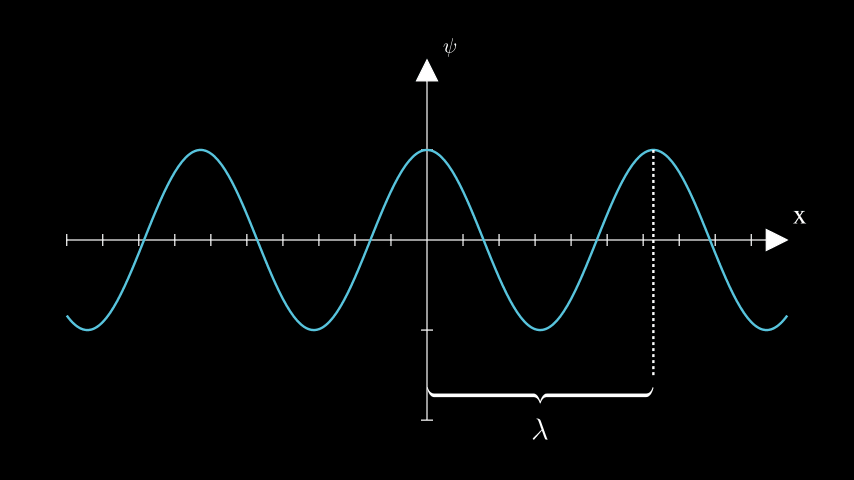
Since it can be whatever, we can use it to add some information about the wave to our notation. For example, a wave should have some length (λ). That is a distance (x) in space, in which it makes a full cycle.

We can encode that information in α, like this:

It’s written like that so that when x becomes equal to λ, the argument of the cosine becomes 2π, which means it’s back at its original value (like in x=0). Kanonically, 2π/λ is simply being written as k. Kanonically, get it?

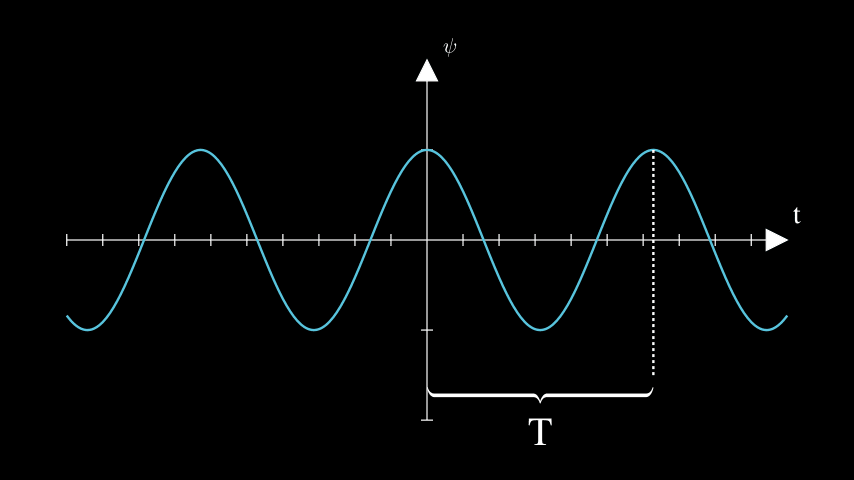
Also, waves have a period (T). Similarly to length, this is the distance in time (t), when the wave makes a full cycle.

This time we can encode that info like so:

Again, when t becomes equal to T, the argument of the cosine becomes 2π and we made full circle. 2π/T is typically written as ω.

Ok, so far so good. Now, waves exist both in time and space, so we can do one more thing here and that is combine the two domains by adding them together (or subtracting).

Doing that makes the wave truly run. Let’s see that by standing in place and letting time flow:

Seems like it’s going to the right, which is what we expect with -ωt. If we wanted it to go to the left we would write +ωt.

And that’s exactly what happens when a wave reflects from a surface. It goes to the right, hits a wall and bounces to the left, like so:

At the top, we can see the right (blue) and left (red) waves moving past each other. At the bottom, we see the two combined. And look, they’re bouncing up and down, but stand still otherwise. This is especially visible at the nodes, which are constant both in space and time.

Got it? Good. Now, back to Hertz.

Being very aware of the mathematics behind standing waves he tried positioning his mirror in such a way, that would make the signal bounce back and overlap with itself.

Once he convinced himself that his setup was correct, it was time for the final, grand test. He took his bull ring and moved it along the suspected path of the standing wave. He expected no power, so no sparks, where the nodes were, but solid sparks where the amplitude moved up and down. It went like this:

Boom! Waves caught in the act of standing around.

Try and make particles do that.

With detecting standing waves Hertz finally did it. He showed that what travels between transmitter and receivers behaves like a wave and a wave it is indeed.

One last thing to note is that Maxwell’s waves were supposed to have the speed value close or equal to that of light. Hertz needed to determine that as well.

While consciously omitting all the maths, we can say that the solution to the wave equation with the wave represented by kx and ωt, will tell us that the speed of that wave will be:

Here f would the frequency and the inverse of T. Through a strange coincidence the unit in which we measure the frequency is the Hertz (the number of times something happens per second).

Hertz knew f because he has built the transmitter and receiver in such a way get him the frequency he wanted. He just didn’t know the wavelength. However, moving the receiver along the standing wave allowed him to measure just that.

Combining the two, he got a value of around 320 000 km/s. Awfully close to the speed of light. Close enough to leave little room for doubt.

All in all, it took him a moment and a half, but he demonstrated what other could not and not for lack of trying. Light is made up of electromagnetic waves and they do exist.

While pleased with himself, Hertz also downplayed the magnitude of his findings with words like these:

…this is just an experiment that proves Maestro Maxwell was right—we just have these mysterious electromagnetic waves that we cannot see with the naked eye. But they are there.

Also, being a scientific entity, through and through, he labored for the sake of truth alone. When asked about the usefulness of his discoveries, he simply replied that:

I do not think that the wireless waves I have discovered will have any practical application.

Though it’s completely unjustified, it’s also impossible not to laugh deep in your heart at this statement, given where we are today.

Nonetheless a profound mystery of Nature was finally revealed and Maxwell’s electrodynamics was, at last, validated.

During his experiments, Hertz made one more stunning discovery, one that would refute the very thing he just tried to prove. I won’t spoil it now, but rest assured that we’ll come back to this in a future episode of Physics Rediscovered.

See you there!