
Quick intro
LeetArxiv is Leetcode for implementing Arxiv and other research papers.
This paper features in both our Reversible Computing Series and Cryptography Series :
Reversible Computing Series
Logical Reversibilty of Computation : This paper laid the foundation for Quantum, Thermodynamic and Catalytic computing.
Generators for Certain Alternating Groups With Applications to Cryptography(we are here) - Introduces the idea of symmetric groups for Catalytic computers and proves that all boolean functions can be transparently computed.
Cryptography Series
Lehmer’s Continued Factorization Algorithm : This paper introduces a factorization algorithm using Continued Fractions.
Asymptotically Fast Factorization of Integers : This paper introduces Dixon’s algorithm for integer factorization.
Generators for Certain Alternating Groups With Applications to Cryptography(we are here) - Proves that simple binary permutations make great, cryptographically secure ciphers.
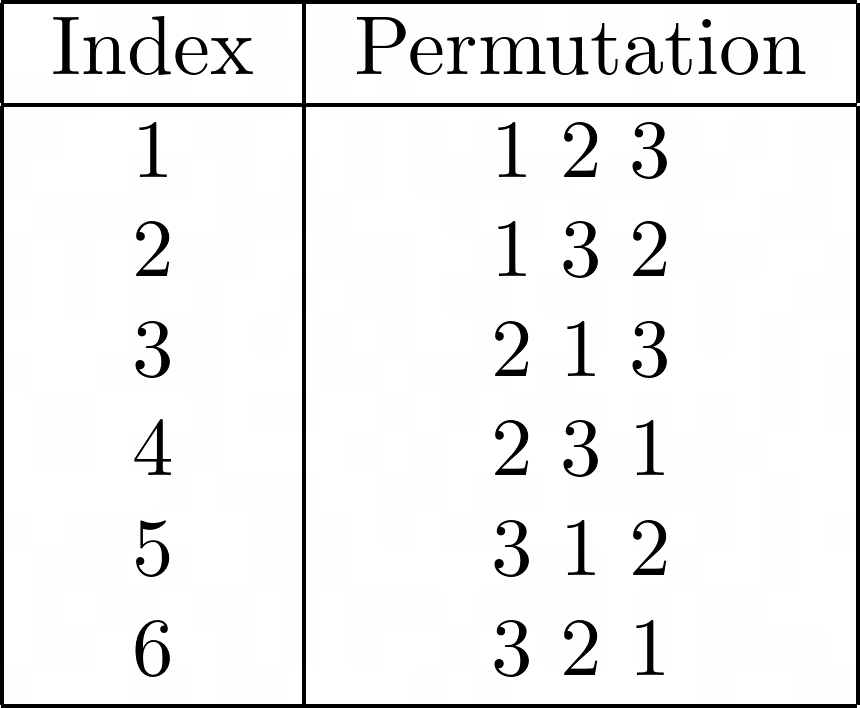
In group theory, the symmetric group, denoted by Sn, is the set of all permutations. The size* of the symmetric group is n!
*The word, ‘order’ means the size of the group while ‘!’ is the factorial.
For example, the symmetric group S3, has an order of 3! = 6 and is the set of all permutations of {1,2,3}
In C, we can use simple recursion to generate the symmetric group of n.
*Note that 12! is the largest value an int takes.
The authors also introduce the concept of basic functions : subsets of the symmetric group of n whose members are part of the set of simple reversible transformations.
Basic functions have these properties :
Basic functions generate the group of even permutations.
A group is a mathematical set where only one operation, mostly addition or multiplication is well defined.
The order of the set of basic functions is ½ × (2n!)
All basic functions are simple and quick to be computed on a computer.
All basic functions are involutions.
Involution means the function is it’s own inverse. i.e you apply it twice to get back where you started.
The authors introduce cycle notation of permutations to further articulate their theorem.
As mentioned by NIST, a 2×n matrix can be used to explicitly represent permutations of a set.
For instance, in the matrix below, the first row represents the original set {1,2,3,4,5,6,7,8} while the second row represents a specific permutation of the set :
In cycle notation, the elements in each cycle are put inside parentheses, ordered so that σ(j) immediately follows j or, if j is the last listed element of the cycle, then σ(j) is the first element of the cycle.
In cycle notation, the example above is written as :
One reads the example as : 1 maps to 3, 3 maps to 2, 2 maps to 5, 5 maps to 7. 4 maps to itself, 4. 6 maps to 8.
As mentioned in the paper, a cycle of length n is called an n-cycle.
Cycles of length 1 are fixed points. They are often dropped from the cycle notation. So, in the wild, the example omits the 4 to be rewritten as :
A cycle of length 2 is called a transposition. Any permutation can be expressed as a product of transpositions.
*This representation is not unique. ie. lots of different transpositions express the same permutation.
With this information, the paper finally defines the alternating group as the subgroup of permutations expressible as a product of an even number of transpositions, denoted by Ax.
*Note that 3-cycles alos generate Ax.
The alternating group, Ax, has an order of ½ × (X!)
Pay attention. This is confusing. But. I didn’t make the rules.
If k is odd, then the cycle is even.
If k is even, then the cycle is odd.
So a 3-cycle is even while a 6-cycle is odd.
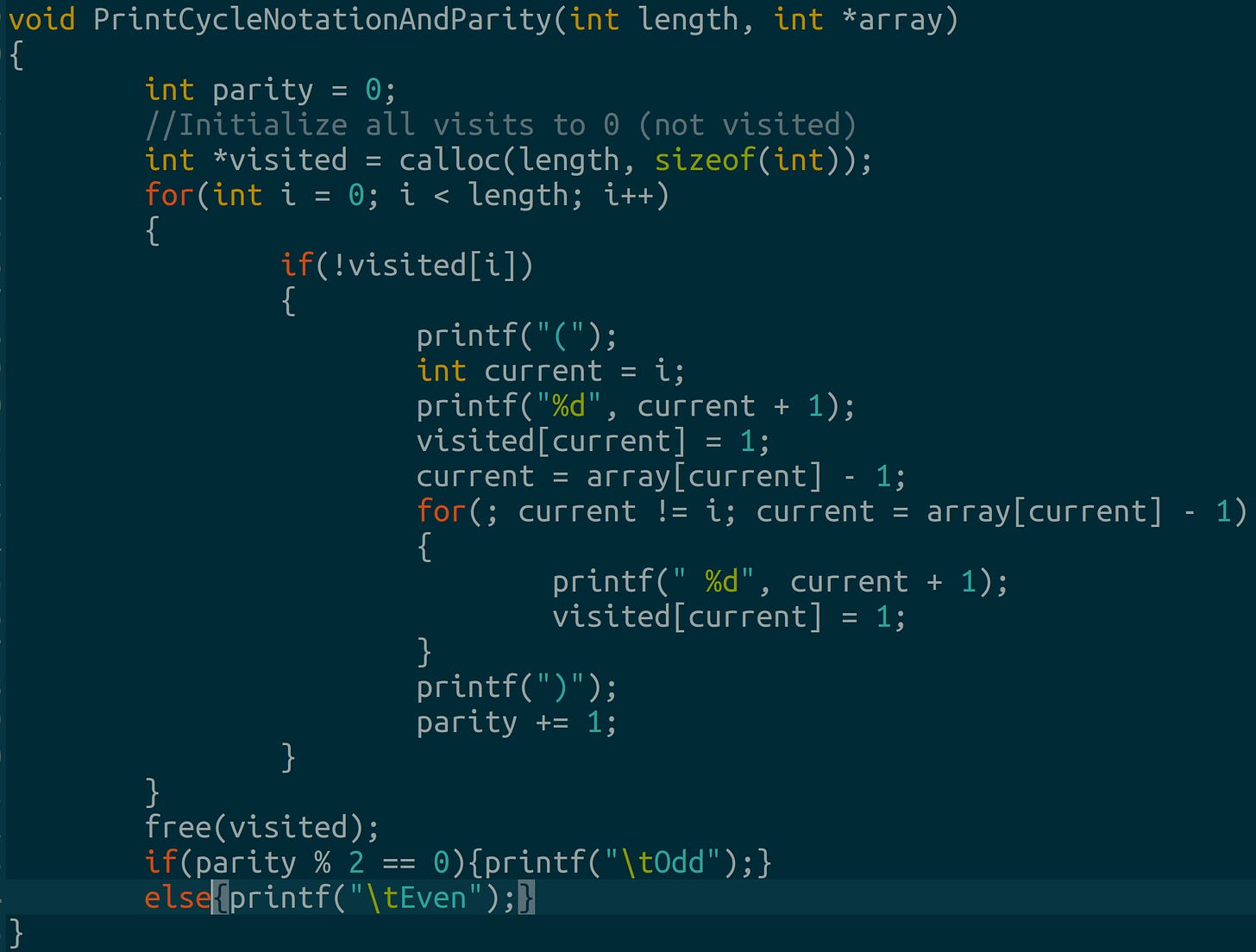
We write a simple cycle notation finder this way. We use an array to check if a permutation element has been visited. Then we maintain a count of all observed k-cycles (including 1-cycles).
Add this function just below where we printed our permutations in section 1.0. You get this once you run your code :
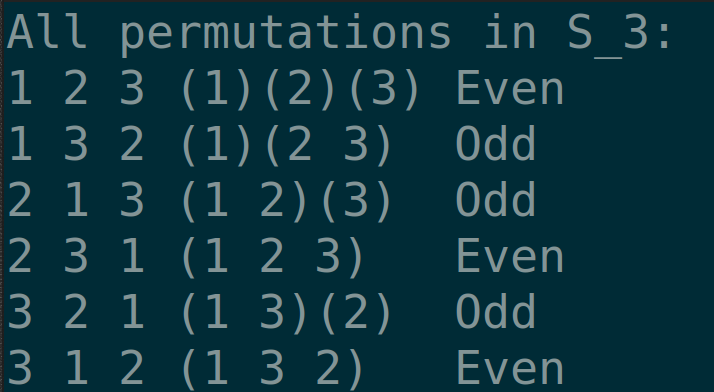
I bet you already saw this in the example above :
There are 3 (exactly half) even and odd cycles in this symmetric group.
1-cycles don’t appear IRL but they matter when counting parity.
The largest possible k-cycle in a symmetric group is the order of the group.
Try to see if you can figure out which permutations are in the alternating group in this example :)
First, the authors define k-functions as a subset of the basic functions used to build a cryptographic cipher.
*It’s not explicitly stated IMO but k-functions are binary (1’s and 0’s) strings.
Their theorem states that the subgroup generated by k-functions is equal to the alternating group given some conditions.
If you’re a programmer interested in catalytic computing, this theorem states that any Boolean function can be computed reversibly with exponential-size programs and constant workspace.
You can try building a cryptographic cipher or
Cited as
Kibicho, Murage. (April 2025). Chapter 6 : Floating-Point Numbers in Residue Number Systems. A Super Friendly Guide to Finite Fields for programmers. LeetArxiv. https://leetarxiv.substack.com/p/floating-point-numbers-in-residue.or
@article{Kibicho2025Chapter6:FloatingPointNumbersinResidueNumberSystems, title = "Chapter 6 : Floating-Point Numbers in Residue Number Systems.", author = "Kibicho, Murage", journal = "LeetArxiv", year = "2025", month = "April", url = "https://leetarxiv.substack.com/p/floating-point-numbers-in-residue" }.png)




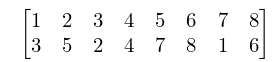
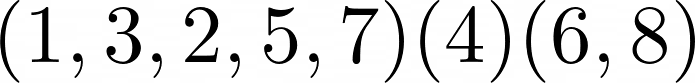
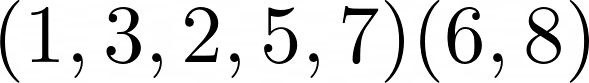


![Braid groups are cool [pdf]](https://news.najib.digital/site/assets/img/broken.gif)
