.png)
5 hours ago
2
If you've taken a calculus class your professor might have explained to you the idea of a monotone function, or (in one direction) a nondecreasing function. A monotone function looks like this:
A monotone function f between two ordered sets, is one which satisfies:
Note that this definition does not imply that f is increasing: it's okay if x < y and f(x) = f(y) (for example, a constant function is monotone), it's just that it's nondecreasing.
In a calculus class, you probably only learned about this concept in the context of functions from real numbers to real numbers, but it's a coherent idea, and a useful abstraction, for any two ordered sets. For example, in set-to-set functions, it shows up a lot in the database literature via ideas like the CALM Theorem. The CALM theorem is interested in monotonicity from the perspective of programs: if getting more inputs can only result in new outputs (the classic example is "if you add more edges to a graph, you can only get more not cycles, not fewer").
One way you might think about what a monotone function f gives you is that knowing the values of f(x) and f(y) is a sort of hint that suggests what the ordering of x and y are. Looking at the the contrapositive of our definition tells us what we can learn from a comparison of f(x) and f(y):
Original statement:
Contrapositives:
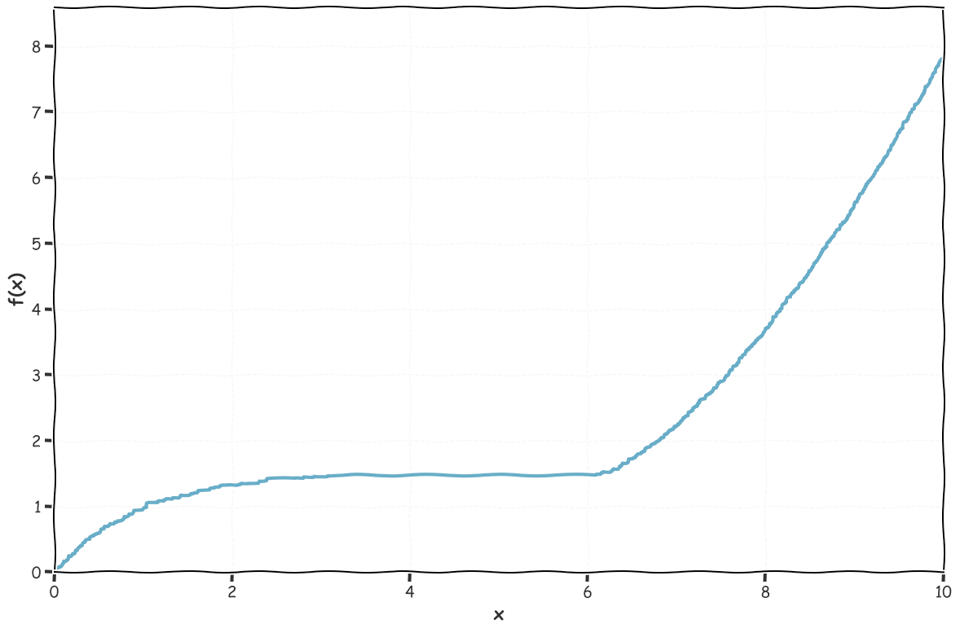
Implied: we don't learn anything if f(x) = f(y). Looking at our graph from before, we see this is true, if we have two points on the plateau (roughly around [4, 5]), they can agree along the y-axis, but be in either order along the x-axis.
The comparison of x and y is in some sense "pickier" than the comparison of f(x) and f(y): there are some things look the same under f(x) and f(y), but can be distinguished in their original forms of x and y.
What this suggests is that if we have a monotone function where comparisons on its codomain are easier or faster to compute than those on its domain, we can use those instead and only fall back to the original comparison when the values are the same.
Our implementation looks like this:
That's all abstract. Let's get more concrete.
A string, in at least some programming languages, is a struct containing a pointer, a capacity, and a length. If we have an array of strings, what we really have is an array of pointers and capacities and lengths, where those pointers point somewhere into heap memory:
What this means if we want to sort this list is that we're not operating on a big slab of continuous memory like it might look like: every time we compare two strings, we have to follow each of their pointers and leap off somewhere into heap memory to compare them. This is not the biggest deal, but if the page we try to read is not in cache, then we're likely to hit a page fault and have to load it in, which is slow.
You can extend this situation to rows in a database which might not even reside in memory and need to be fetched from disk, or even network: comparing two of them might need to read data from some far off place.
There is a well-known trick to improve this situation, which I know most commonly as an abbreviated key: store a small prefix (8 bytes is a good number) of the string next to its pointer:
Now we've duplicated some of the data: some of the string is actually stored directly in our big slab of memory. The heart of the trick is that the operation of "taking a fixed-size prefix" is monotone!
Consider if we take 3-byte prefixes of strings, and we have the following dataset:
If we store our prefixes inline, they look like this:
Now, comparing "goofball" and "goofy," we have to go to the actual string to distinguish, since they agree on their prefix. But because of monotonicity, and the fact the "don" < "goo", we know already that "donald" must come before "goofy" without ever having to do any pointer-chasing.
We can observe this:
This is of course unfair and a best-case situation for this technique, as all the words are different and almost all of them are different within the first 8 characters, so we almost never have to read the actual string. If we had to do that more often (say, if all the strings had the same first 8 characters), this inlining would contribute almost pure overhead.
We can confirm this by making it so:
Which degrades our performance, as we'd expect:
- See Brandur Leach's excellent post on SortSupport in Postgres and the follow-up of implementing it for INET types.
- A related topic is German Strings, which stores small strings inline in the data used by the pointer.
